На основные фотоэлектрические параметры солнечных элементов, такие, как вольт-амперная характеристика и спектральная чувстви­тельность, влияют как оптические, так и электрофизические свой­ства полупроводника. Лишь детальный анализ позволяет опреде­лить, чем^ вызванзг недостаточно высокая эффективность данного солнечного элемента. Однако для этого прежде всего необходимо измерить основные его характеристики, что даст возможность по­нять причины возникновения, природу и преобладающий вид потерь.

Вольт-амперная характеристика

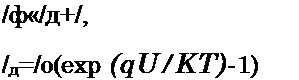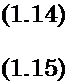Уже в первых работах, посвященных теории и экспериментальному изучению свойств солнечных элементов, было показано, что вольт — амперная характеристика солнечного элемента отличается от вольт — амперной характеристики полупроводникового диода появлением чле­на /ф, обозначающего собой ток, генерируемый элементом под дей­ствием освещения, часть которого /д течет через диод, а другая часть / — через внешнюю нагрузку:

обычная темновая характеристика, в которой /0 — обратный ток на­сыщения р—«-перехода; д — заряд электрона; Т — абсолютная тем­пература; К — постоянная Больцмана; [/ — напряжение. При разом­кнутой внешней цепи, когда ее сопротивление бесконечно велико и 7=0, по уравнению (1.14) можно определить напряжение холо­стого хода солнечного элемента:

Uxx=ln (h/Io+i)KT/q.

Для реального солнечного элемента характерно наличие после­довательного сопротивления /?п, которое складывается из последова­тельно включенных сопротивлений контактных слоев, сопротивле­ний каждой из р — и п-областей элемента, переходных сопротивлений

2ММ Колтун
металл—полупроводник, а также шунтирующего сопротивления НШ1 отражающего возможные поверхностные и объемные утечки тока по сопротивлению, параллельному р—и-переходу. Учет этих сопро­тивлений и рекомбинации в р—тг-переходе приводит к развернутому

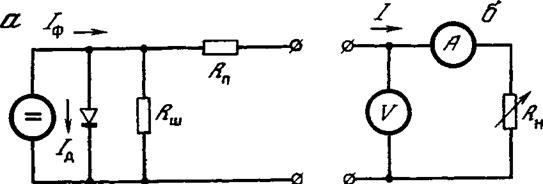Рис. 1.17. Эквивалентная (а) и измерительная (б) элект­рические схемы солнечного элемента

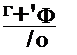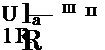выражению для вольт-амперной характеристики, в которое введен коэффициент А:

Уравнение (1.16) можно записать в более удобном для практи­ческого использования виде:

ентную и измерительную схемы

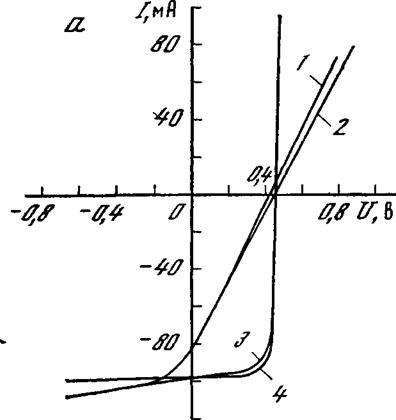
геристик по формуле (1.17) [67] лияние последовательного и шун — ойства солнечных элементов Ре­ны на рис. 1.18. Выходная мощ­енного элемента, может быть оце — ффициентом заполнения вольт-ам — ает степень приближения формы ^ прямоугольной: £^0,8—0,9 озна- <ой выходной мощностью. У совре — элементов коэффициент £ обычно 1 шунтирующего сопротивления от лого, как і? ш=100 Ом, сравнитель — ьт-амперной характеристики (см. входную мощность солнечного эле — з изменение последовательного со­до 7?п=5 Ом, приводит к резкому эй характеристики и значительно-

I.

В дальнейшем как световая, так и темновая вольт-амперные ха­рактеристики солнечного элемента подверглись еще более деталь­ному анализу. Было обнаружено, что в зависимости от уровня на­пряжения механизм протекания обратного тока насыщения через р—п-переход меняется. Как правило, этот ток представляет собой сумму двух токов. В связи с этим предложено записывать уравне­ние вольт-амперной характеристики солнечного элемента в следую­щем виде [68]:

—l) + /02(expги)~ 1)~“

где /о! — обратный ток насыщения, определяемый диффузионным механизмом протекания тока через тонкий р—/г-переход [69]; 102 — обратный ток насыщения, возникающий вследствие рекомбинации в области р—^-перехода [70], при этом обычно коэффициент А =2.

Разработан ряд достаточно точных методик, позволяющих по измеренным световым и темновым вольт-амперным характеристикам солнечных элементов рассчитать значения /0, і? п, коэффициен­та А [15, 16, 21, 71] и выявить тем самым физические процессы, приводящие к недостаточно высокой эффективности солнечных эле­ментов из определенного полупроводникового материала.

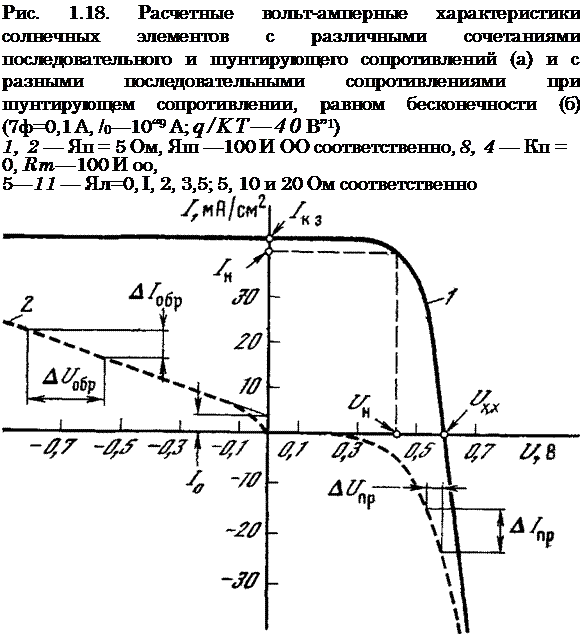
На рис. 1.19 представлена типичная вольт-амперная характе­ристика: световая (измеренная на имитаторе внеатмосферного Солн­ца) ‘и темновая (измеренная с приложением внешнего смещения в темноте в прямом (IV квадрант) и обратном (II квадрант) направ­лениях). Часть световой характеристики, расположенной в I квадран­те, и ее продолжение (IV квадрант) представляют собой прямую линию. Наклон этой прямой к оси токов характеризует последова­тельное сопротивление солнечного элемента

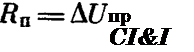пр с»

где At/np с и Д/Пр с измеряются в области, близкой к Uxx.

Часть световой характеристики в I квадранте и ее продолжение (II квадрант) тоже являются прямой линией. Наклон ее к оси напряжений характеризует собой шунтирующее сопротивление сол­нечного элемента

jRm — A U пр — с/Д/

где Д£/прс и А/др с измеряются в области, близкой к /кз.

В связи с тем, что на световой вольт-амперной характеристике наклон прямой около точки /кз измерить трудно, определение і? ш обычно проводят по наклону темновой вольт-амперной характери­стики (штриховая кривая во II квадранте):

#ш= Д£^обр /А^обр •

Построение темновой характеристики позволяет также найти об­ратный ток насыщения /0. Отрезок на оси ординат от начала коор-

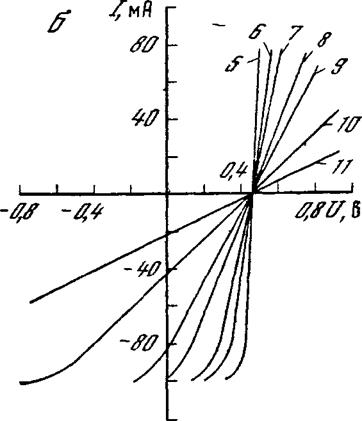Рис. 1.19. Типичная вольт-амперная харак­теристика современного кремниевого солнечного элемента при измерении на имитаторе внеатмос­ферного Солнца

1 — световая,

2 — темновая

динат до точки пересечения с продолжением линейного участка об­ратной ветви темновой характеристики дает значение h.

Поскольку, однако, р—тг-переход солнечного элемента в рабочем режиме включен в прямом направлении (воздействие светового из­лучения, появление благодаря ему избыточного количества нерав­новесных носителей в областях полупроводника по обе стороны р—п-перехода аналогичны подключению напряжения в прямом на­правлении), правильнее определять ток насыщения, а также рас­
считывать коэффициент А по прямой ветви темновой вольт-ампер — ной характеристики или по световой вольт-амперной характеристи­ке (называемой также нагрузочной световой характеристикой эле­мента) .

Для первого из этих методов можно воспользоваться темновой характеристикой диодаг представляемой выражением (1.15), запи­сав его в виде уравнения прямой в отрезках:

In (/« + /о) = In /о -j—акт ^*

%

Это уравнение применяется при расчетах только в случае боль­ших токов (когда /д>/0), а также рекомбинационного механизма протекания обратного тока насыщения через р—^-переход [70], в связи с чем в знаменатель показателя экспоненты в уравнении (1 15) вводится, как уже указывалось, коэффициент А. Участок больших токов и напряжений (характерных для рабочей нагрузоч­ной точки солнечного элемента) прямой ветви темновой характери­стики используется для построения зависимости 1п/д=/(£/). Тангенс угла наклона этой прямой равен q/AKT, а отрезок, отсекаемый на оси ординат, дает значение 1п/0.

Имеется еще один метод определения /о и А в условиях, близ­ких к рабочим условиям использования солнечного элемента. При этом методе световая вольт-амперная характеристика измеряется при нескольких (хотя бы двух) разных плотностях падающего излуче­ния от имитатора Солнца.

Запишем уравнения (1.14) и (1.15) с учетом падения напря­жения на последовательном сопротивлении и рекомбинации в р—п — переходе:

1=1 о (exp (q(U-IRn) /АКТ) -1) -7ф. (1.18)

В режиме ‘холостого хода 7=0, ії~ихх, а при Rn=0 фототок /* можно считать равным /кз. Тогда

In (IK3+I0)=lnh+qUxJAKT.

При каждом новом значении плотности потока излучения имита­тора Солнца, устанавливаемом с помощью эталонного солнечного элемента с линейной зависимостью тока короткого замыкания от освещенности, измеряются значения /«з и Uxx исследуемого солнеч­ного элемента. Строится зависимость 1п/кз от Uxx. Тангенс угла наклона этой прямой равен q/AKT, а на оси ординат ею отсекается значение In/о.

Таким образом, из световых вольт-амперных характеристик уда­ется также определить параметры А и /0, причем именно те их зна­чения, которые характерны для солнечных элементов в рабочем режиме

Уточненный и вместе с тем достаточно простой метод опреде­ления Ей, /?ш, А и /0 предложен в работе [71]. Необходимо изме-

рить вольт-амперную характеристику солнечного элемента лишь при •одном значении плотности потока излучения и затем вычислить: обозначаемую Р0 площадь под кривой зависимости £/=/(/), пред­ставляющей собой вольт-амперную характеристику; наклон кривой U=f(I) при /=0, определяющий tga=AKTIqIK3+Rn; площадь Pi под кривой зависимости мощности элемента IU от тока /. После­дующий расчет производится по формулам, указанным в публика­ции [71].

Оптические излучения различных длин волн проникают на разную глубину (поскольку эта величина существенно зависит от энергии квантов) и создают свое пространственное распределение рожден­ных светом пар электрон—дырка (см. рис. 1.1, 1.2). Дальнейшая судьба рожденных пар зависит от их диффузионной длины в дан­ном полупроводниковом материале. Если она достаточно велика, то созданные светом избыточные неосновные носители заряда успеют (даже без участия тянущего электростатического поля) только за счет процесса диффузии дойти до области р—тг-перехода и будут разделены его полем. Решающую роль в эффективности этой стадии преобразования оптического излучения внутри полупроводника играет соотношение между диффузионной длиной L и расстоянием от р—w-перехода Z, на котором создаются светом пары электрон — дырка.

Рассмотрим два крайних случая расположения р—/г-перехода в полупроводниковом кристалле по отношению к направлению паде­ния оптического излучения: перпендикулярно (рис. 1.15, а) и па­раллельно (рис. 1.15,6). Условимся, что в первом случае свет про­никает на всю глубину кристалла и Z равно толщине полупровод­никовой пластинки, а во втором — освещается вся поверхность пла­стинки шириной d.

Очевидно, что эффективность собирания для перпендикулярного и параллельного расположений р—/г-перехода определяется соответ­ственно соотношениями

1=(Ln+Lp)ll и 7=(L„+Lp)/d.

На первый взгляд параллельное расположение кажется более предпочтительным, ибо для полного собирания и разделения носи­телей наиболее существенным является распределение пар носите­лей в направлении, перпендикулярном р—/г-переходу: равномерная генерация носителей по глубине кристалла создает благоприятные условия для их диффузии к р—/г-переходу и последующего про­странственного разделения. Разработанные на основе такого рас­положения р—/г-перехода по отношению к свету многопереходные матричные солнечные элементы, состоящие из большого числа мик­роэлементов, плоскости которых параллельны по отношению к па­дающему солнечному излучению (или расположены под небольшим углом к нему) действительно обладают высокой эффективностью собирания носителей в длинноволновой области спектра и позволя­ют получить значительную фото-ЭДС с единицы освещаемой по­верхности [64, 65]. Однако расчетным и экспериментальным путем было установлено, что из-за весьма небольших размеров микроэле­ментов рекомбинация созданных светом пар на освещаемой поверх­ности играет при параллельном расположении р—/г-перехода отно­сительно падающего излучения значительно большую роль, чем при

перпендикулярном. Вследствие этого для увеличения эффективно­сти собирания в коротковолновой области спектра необходимо со­здать на обращенной к свету поверхности дополнительный слой, легированный примесью противоположного типа проводимости, т. е. использовать частично структуру с перпендикулярным расположе­нием р—тг-перехода [66].

Если при параллельном расположении концентрация созданных светом пар М убывает от поверхности в глубь полупроводника как в п-, так и в p-области, то при перпендикулярном расположении это характерно лишь для обращенной к свету области кристалла, например тг-области, в то время как в p-области наибольшее коли­чество пар образуется у р-п-перехода. Концентрация пар на глуби­не I подчиняется соотношению, полученному в результате диффе­ренцирования выражения (1.3):

M=N0a exp (—аI),

где No—’число квантов, падающих на единицу поверхности полу­проводника. Концентрация пар, уменьшающаяся в глубину полу­проводника, может быть подсчитана для области поглощения полу­проводникового материала с помощью зависимости а(Е) (см. рис. 1.1). Результаты таких расчетов для кремния, выполненных при нескольких значениях длины волны, показаны на рис. 1.16 15]. Вертикальные линии, ограничивающие области, определяемые диффузионной длиной носителей в материале п — и p-типа, позволя­ют наглядно оценить процесс собирания носителей заряда при пер­пендикулярном расположении р-п-перехода относительно падаю­щего излучения (см. рис. 1.15,а).

Ординаты точек на построенных кривых пропорциональны аехр (—а/), абсциссы — расстоянию в глубь полупроводника от осве­щаемой поверхности, площадь между осями и каждой из кривых — потоку падающих квантов, а площадь, ограниченная кривой и орди­натами, соответствующими 1=1Л+Ьп и 1=1Л—ЬР (заштрихованная часть),—току короткого замыкания кремниевой пластинки с р—га — переходом.

Таким образом, отношение заштрихованной площади к общей площади под кривой дает возможность в соответствии с соотноше­нием (1.13) определить эффективность собирания f (при условии, конечно, что квантовый выход фотоионизации |}=1).

Планарная конструкция солнечных элементов, изображенная на рис. 1.15, а, стала основной и получила наибольшее распростране­ние. Такие солнечные элементы были созданы из самых разнооб­разных материалов, причем направления оптимизации этой конст­рукции можно легко определить, анализируя результаты расчетов, аналогичные выполненным для кремния и представленным в графи­ческой форме на рис. 1.16.

Очевидно, что для повышения | и /кз необходимо увеличивать диффузионную длину неосновных носителей заряда по обе стороны

-у——■’ 1 1 ..

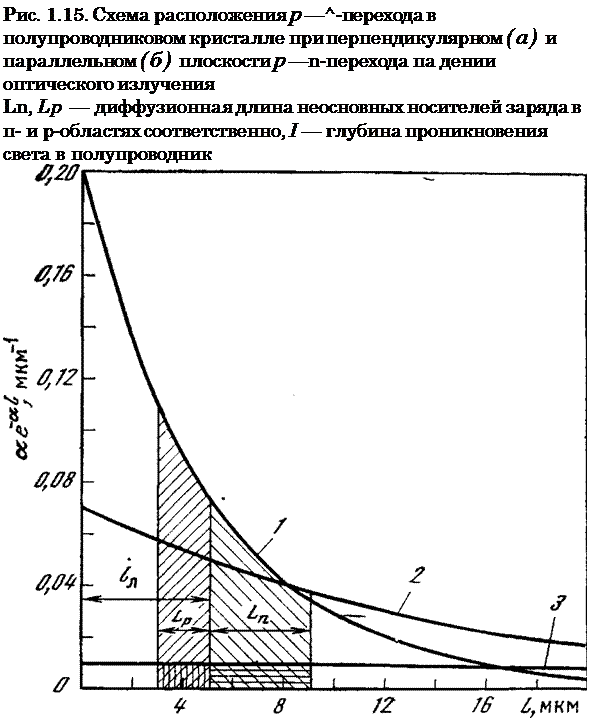Рис, 1.16. Распределение числа созданных опти­ческим излучением пар электрон—дырка по глу­бине кремния при паде­нии излучения разной длины волны перпенди­кулярно плоскости р— п-перехода

2 — 0,619 мкм,

а = 2000 см-1,

2 — 0,81 мкм, а = 700 см-1;

3 — 0,92 мкм, а = 90 см-1

р—w-перехода (Ln и Lp), что может быть достигнуто выбором соот­ветствующих исходных материалов и сохранением высоких значе­ний L в процессе изготовления р—п-перехода. При невозможности увеличить L в области полупроводника, примыкающей к освещае­мой поверхности {Lp на рис. 1.15), необходимо приблизить р—п — переход к освещаемой поверхности, чтобы удовлетворялось соотно­шение Lp>ln, где 1Л — глубина р—тг-перехода, и все созданные све­том носители заряда могли быть собраны и разделены полем р—п — перехода. Современные технологические методы обеспечивают малую глубину р—и-перехода [5, 13, 21].

Подобное же условие следует выполнять и для базовой области солнечного элемента (расположенной за р—^-переходом). Толщина

солнечного элемента, определяемая в основном базовой областью, не должна быть меньше глубины проникновения в полупроводник излучения длинноволновой части фотоактивной области спектра (энергия квантов Av>£g), а диффузионная длина неосновных но­сителей заряда в базовой области должна соответствовать толщине элемента и глубине проникновения света.

Измерение тока короткого замыкания солнечного элемента одновре­менно с исследованием спектрального состава ц плотности падаю­щего на элемент оптического излучения позволяет сделать вывод об эффективности различных стадий процесса преобразования излуче­ния в электрическую энергию, происходящих внутри элемента.

Прежде всего, конечно, полезно условиться о том, по отношению к какому — падающему или поглощенному —- потоку излучения про­изводится оценка рассматриваемых процессов. В пределах линейной зависимости тока короткого замыкания солнечного элемента от плотности потока излучения справедливо соотношение

/кз2(М=^кзі(Я)/(1~г(Я)),

где /кз2(Я), Ікзі(К) —ток короткого замыкания солнечного элемен­та при заданной интенсивности соответственно поглощенного и па­дающего излучения; г(X) — коэффициент однократного отражения. Все три величины отнесены к одной и той же определенной длине волны.

Для нахождения г(Х) необходимо знать п и А;, а в области основ­ной полосы поглощения, где к мало, достаточно иметь лишь данные о показателе преломления п. Для сравнительно малоизученных полу­проводников, когда известно только значение ширины запрещен­ной зоны Eg и оптические константы еще не определены, мож­но воспользоваться для вычисления п эмпирическим правилом Мосса [25]:

Egnk—173.

Весьма полезна для анализа и оценки качества солнечного эле­мента такая характеристика, как спектральная зависимость тока ко­роткого замыкания элемента, рассчитанная на один квант погло­щенного света. Эту величину обычно называют эффективным кван­товым выходом солнечного элемента (>Эф. Если N0 — число квантов, падающих на единицу поверхности полупроводника, то

фэф — /к S2/N

где Іц з 2 измеряется в электронах в секунду, а фэф выражается в электронах на квант (фотон).

Эффективный квантовый выход элемента зависит от двух пара­метров:

&Ф=Рї, (1.12)

где р — квантовый выход внутреннего фотоэффекта, определяемый числом пар электрон—дырка, создаваемых внутри полупроводника каждым поглощенным квантом за счет процесса фотоионизации; 7 — эффективность собирания носителей (или, иначе, коэффициент разделения носителей) потенциальным барьером р—«-перехода, по­казывающая, какая часть из общего числа пар, созданных оптиче­ским излучением, участвует в формировании тока короткого замы­кания солнечного элемента при подключении внешнего регистри­рующего прибора.

Принято считать квантовый выход фотоэффекта равным едини­це, если каждый поглощенный квант создает одну пару электрон — дырка. Результаты выполненных с высокой точностью измерений квантового выхода внутреннего фотоэффекта для кремния пред­ставлены в работе [61] и подробно обсуждены в публикации [62]. Для этих измерений была собрана прецизионная установка, позво­лявшая одновременно измерять ток короткого замыкания полупро­водниковых кристаллов с р—/г-переходом и суммарное (диффуз­ное + зеркальное) отражение от их поверхности. Спектр падающего на кристалл оптического излучения измерялся с помощью зеркаль­ного монохроматора, для создания заданной температуры кристал­ла применялись криостат и электрическая печь, а для определения энергии квантов — калиброванный термостолбик. Отраженное от по­верхности кристаллов излучение в видимой и ультрафиолетовой об­ластях спектра (до длины волны 0,254 мкм) регистрировалось

1.4. Преобразование излучения в электроэнергию ■ 11 1 -■■■- … ……………………………….. " 1 ………….. ………………… — — ……………………………. …….. ……… ■■■

пластинкой с люминофором и установленным за ней фотоумножи­телем.

Квантовый выход внутреннего фотоэффекта рассчитывался па формуле

{*=/к31/(1-г)дЛ^, (1.13)

где q — заряд электрона, поскольку /к 31 выражен в энергетических единицах.

Эти измерения^ были выполнены на кристаллах с р—я-переходом, в которых фотоэлектрический эффект обнаруживается сразу — па генерируемому в цепи току без приложения внешнего смещения. Обеспечивались условия, когда эффективность собирания носителей 7=1 (или но крайней мере сохраняет постоянное значение во всем использованном диапазоне спектра), чтобы при расчете можно было пользоваться формулой (1.13). В связи с этим для экспериментов выбирались кристаллы с большой диффузионной длиной неосновных носителей заряда в верхнем легированном слое Ьл, Глубина зале­гания р—/г-перехода 1Л была небольшой, и соблюдалось условие ЬЛ>1Л. К тому же эксперименты проводились только в видимой и ультрафиолетовой областях спектра.

В результате анализа полученных экспериментальных данных был сделан вывод, что в широком диапазоне энергии падающих квантов (EgChv<2Eg) квантовый выход, обусловленный фотоиони­зацией, р в кремнии равен единице. При большой энергии квантов падающего излучения (fev>2£*, т. е. в ультрафиолетовой области спектра) начинал резко возрастать, что, вероятно, объясняется процессом ударной ионизации — возникновением вторичных пар электрон—дырка за счет избыточной кинетической энергии первич­ных пар.

Таким образом, можно считать, что первый акт взаимодействия оптического излучения с полупроводником (внутри кристалла) про­исходит практически без потерь, с эффективностью, близкой к 100 % г в широкой области спектра. Однако в большинстве полупроводни­ков, использующихся для создания солнечных элементов, несмотря на равный единице квантовый выход фотоионизации (а также при 7>1 в ультрафиолетовой области) с увеличением энергии квантов возрастают потери в расчете на энергию одного кванта "в силу ко­нечного значения ширины запрещенной зоны обычного полупровод­никового материала [63]. Переход к солнечным элементам более — сложной структуры, например на основе каскадных систем, или к элементам с контролируемым градиентом ширины запрещенной зоны по глубине (большой у поверхности полупроводника и уменьшаю­щейся в глубь материала, что отвечает спектральной зависимости коэффициента поглощения) позволяет полностью избавиться от та­ких оптических и энергетических потерь и увеличить КПД преоб­разования солнечного излучения в электрическую энергию.

Полупроводниковый, например кремниевый, солнечный элемент наи­более распространенной конструкции представляет собой систему из двух полупроводниковых слоев с проводимостями р — и /г-типа, находящихся в тесном контакте друг с другом. Переходная зона (граница) между областями с противоположными типами проводи­мости располагается внутри полупроводникового материала и на­зывается электронно-дырочным или р—н-переходом (ранее чаще именовавшаяся запорным слоем).

В состоянии равновесия уровень Ферми во всем материале дол­жен быть одинаковым [9—11]. Это условие обеспечивается двойным заряженным слоем в области р—п-перехода, получившим название слоя объемного заряда, и сопровождающим его электростатическим потенциалом (рис. 1.14). Высота потенциального барьера равна раз­ности положений дна зон проводимости материалов п — и р-типов. Следует отметить, что положение уровня Ферми и, следовательно, высота барьера зависят от температуры и концентрации примесей в полупроводниковом материале по обе стороны р—п-перехода, что, с одной стороны, открывает широкие возможности по направленно­му изменению свойств р—п-переходов, а с другой — определяет до­статочно сильную температурную зависимость его оптических и фо­тоэлектрических характеристик [5, 6].

Оптическое излучение, падающее на поверхность полупроводни­ковой структуры с р—тг-переходом, создает (в основном вблизи по­верхности) пары электрон—дырка, причем концентрация пар по­степенно спадает от поверхности в глубь полупроводника по направ­лению к р—п-переходу. В том случае, когда расстояние от поверх­ности до р—н-перехода меньше глубины проникновения света 1/а, пары электрон—дырка создаются и за р—п-переходом. Если переход отстоит от места возникновения пар на расстоянии, меньшем диф­фузионной длины, то они вследствие диффузии подойдут к р—п — переходу и разделятся под действием его поля. Электроны перейдут в электронную, а дырки—в дырочную часть перехода. На внешних металлических электродах, соединенных с р — и n-областями полу­проводника, появится разность потенциалов, которая вызовет ток через нагрузочное сопротивление [12—16].

Диффундирующие к р—п-переходу неосновные избыточные но­сители тока будут разделяться благодаря наличию потенциального барьера. Скопление избыточных (разделенных переходом) электро­нов в п-области и дырок в p-области фотопреобразователя приводит к компенсации объемного заряда, Сосредоточенного у р—тг-перехода, т. е. к созданию электрического поля, противоположного по направ­лению к существующему.

Таким образом, одновременно с появлением разности потенциа­лов на внешних электродах вследствие освещения происходит из­менение и потенциального барьера, существовавшего в неосвещен-

Рис. 1.14. Структура энергетических зон полупро­водника в области неосвещенного р_—гс-перехода (а) и распределение электростатического потенциа­ла (б)

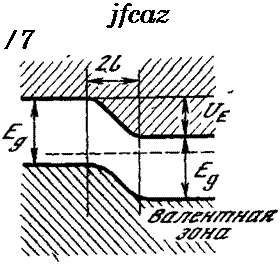21 — ширина области объемного заряда запорного слоя; Ue — равновесный электростатический потенциал на границе п — и p-областей; Eg — ширина запрещенной воны; штриховая линия — равновесное положение уровня Ферми

ном р—и-переходе. Возникающая фото-ЭДС & уменьшает этот барьер, что в свою очередь

приведет к возникновению встречных пото­ков (дополнительно к существовавшим в

равновесии) электронов из электронной и дырок из дырочной частей. Эти потоки практически равноценны току в прямом направлении, возникающему под действием приложенного к р—п-переходу элект­рического напряжения. Таким образом, с момента начала освещения ро мере накопления избыточной (по сравнению с равновесной) кон­центрации электронов в электронной части р—тг-перехода и дырок в дырочной происходит уменьшение высоты барьера, или электро­статического потенциала UE (см. рис. 1.14), что вызывает увеличе­ние тока во внешней нагрузке и возрастание плотности встречных потоков электронов и дырок через р—н-переход. Когда число созда­ваемых светом избыточных пар сравняется с числом пар, уходящих через р—п-переход или во внешнюю нагрузку, установится стацио­нарное состояние. Как правило, это происходит через тысячные до­ли секунды после начала освещения [17, 18].

Фотоэлементы, основанные на фотоэффекте в полупроводниковых структурах с запорным слоем, так называемом вентильном фотоэф­фекте, непосредственно превращают падающее на них оптическое излучение в электрическую энергию, являясь, таким образом, ее генераторами, и в отличие от фотосопротивлений и фотоэлементов с внешним фотоэффектом не нуждаются в источнике внешнего на­пряжения.

Начиная с открытия в середине прошлого века фотоэлектриче­ских свойств селена и создания в конце прошлого и начале нашего столетия на основе" селена и гетеросистемы медь-закись меди пер­вых фотоэлектрических преобразователей светового излучения в не­большие электрические сигналы, делались неоднократные попытки повышения КПД таких преобразователей и превращения их в ис­точник электрической энергии значительной мощности. Усовершен­ствование технологии, а также применение оптических фильтров позволили получить селеновые фотоэлементы, спектральная чувст­вительность которых практически повторяла кривую чувствитель­

ности человеческого глаза. Улучшенные селеновые ‘фотоэлементы нашли широкое применение в качестве фотоэкспонометров в фото — и киноаппаратуре. Однако коэффициент полезного действия фото­элементов не поднимался выше 0,5%. Успешное развитие фотоэлек­трического метода преобразования энергии излучения началось лишь после создания зонной теории электронного строения полупровод­ников, разработки методов их очистки ж контролируемого легиро­вания, выяснения той определяющей роли, которую играет запор­ный слой на границе полупроводников с противоположным типом проводимости. В 1954 г. появилось краткое сообщение о разработке кремниевого солнечного элемента с КПД около 6%, а в 1958 г. на борту советских и американских спутников Земли уже работали кремниевые солнечные батареи, снабжавшие электроэнергией элек­тронную аппаратуру. За прошедшее время КПД солнечных элемен­тов резко возрос, чему способствовали все лучшее понимание фи­зических явлений, происходящих в солнечных элементах, создание все более совершенных технологических приемов их изготовления и разработка новых усовершенствованных конструкций элементов из разнообразных полупроводниковых материалов. В СССР особен­но много для развития фотоэлектрического метода преобразования солнечной энергии сделали Н. С. Лидоренко, А. П. Ландсман, В. С. Вавилов, Ю. П. Маслаковец, В. К. Субашиев, А. М. Васильев, Ж. И. Алферов; в США — П. Раппопорт, М. Принс, Дні. Лоферский, М. Вольф, Г. Раушенбах, Дж. Линдмайер, Г. Брандхорст.

Большинство вентильных фотоэлементов, созданных в первые десятилетия развития фотоэлектричества,— селеновые, сернистогал — лиевые, сернистосеребряные, сернистомедные, германиевые и не­которые другие — используется по-прежнему в основном как индика­торы излучения. Кремниевые фотоэлементы/ а в последнее время и фотоэлементы из арсенида галлия и других широкозонных полу­проводников благодаря высокому КПД, достигающему в настоящее время у лучших образцов 15—22% (а при использовании сложных каскадных систем на их основе даже 27—28% [60]), широко при­меняются как фотоэлектрические преобразователи солнечного излу­чения или солнечные элементы.

Фотоэлектрогенераторы для прямого преобразования энергии из­лучения Солнца в электрическую, собранные из большого числа последовательно и параллельно соединенных фотопреобразователей, получили название солнечных батарей. Современные солнечные ба­тареи генерируют на свету значительную электрическую мощность и применяются как для питания радиосхем, средств связи, счетчи­ков космических частиц, так и для энергоснабжения большинства космических аппаратов и многих наземных автономных устройств различного назначения.

Оптические исследования тонких легированных слоев кремния и других полупроводников было бы значительно легче и точнее вы­полнять с помощью излучения, которое сильно поглощается мате­риалом полупроводника. Таким, например, является ультрафиолетовое излучение с длиной волны 0,2—0,4 мкм, почти полностью погло­щаемое слоями кремния толщиной всего 0,05—0,1 мкм. Однако из­менение концентрации свободных носителей заряда в полупровод­нике в очень широких пределах практически не влияет на его оп­тические свойства в коротковолновой области спектра [58]. Спектры отражения в ультрафиолетовой области помогли установить особен­ности зонной структуры полупроводников. Характерные для многих полупроводниковых материалов всплески отражения объясняются резким ростом показателя поглощения, что вызывается межзонны­ми переходами при большой ширине запрещенной зоны в тех об­ластях зависимости Е от к, где к^О [10, 11, 25],

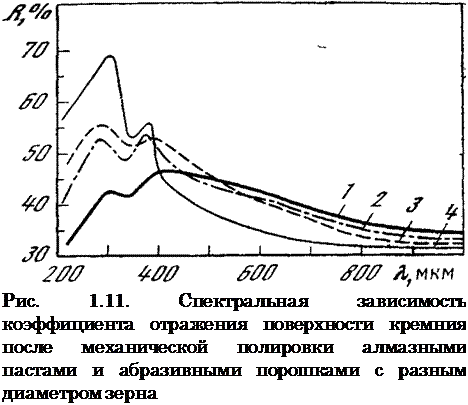
С помощью спектров ультрафиолетового отражения также уда­ется весьма тонко контролировать качество механической и хими­ческой полировки поверхности полупроводниковых кристаллов, что отчетливо видно из приводимых на рис. 1.11 и 1.12 спектральных зависимостей зеркального коэффициента отражения от глубины остающихся после полировки нарушений на поверхности кремния и арсенида галлия. Только после того, как глубина нарушений в результате дополнительной полировки становится меньше длины волны ультрафиолетового (0,2—0,4 мкм) и видимого (0,4—0,75 мкм) излучений, использованных при измерениях (выполненных на спек­трофотометрах СФ-4, СФ-10, СФ-20, СФ-26), коэффициент отраже­ния в этих областях спектра перестает изменяться (см. рис. 1.12).

Высокой эффективности оптического контроля способствует на­личие пиков отражения, имеющихся у кремния и арсенида галлия в ультрафиолетовой области спектра. Например, контроль за состоя-

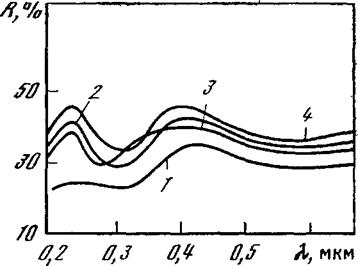J — 3 мкм; 2—1; 3—1; 4 — 0,1—0,2 мкм; 1, 2, 4 — время полировки 1ч; 3 — 2 ч

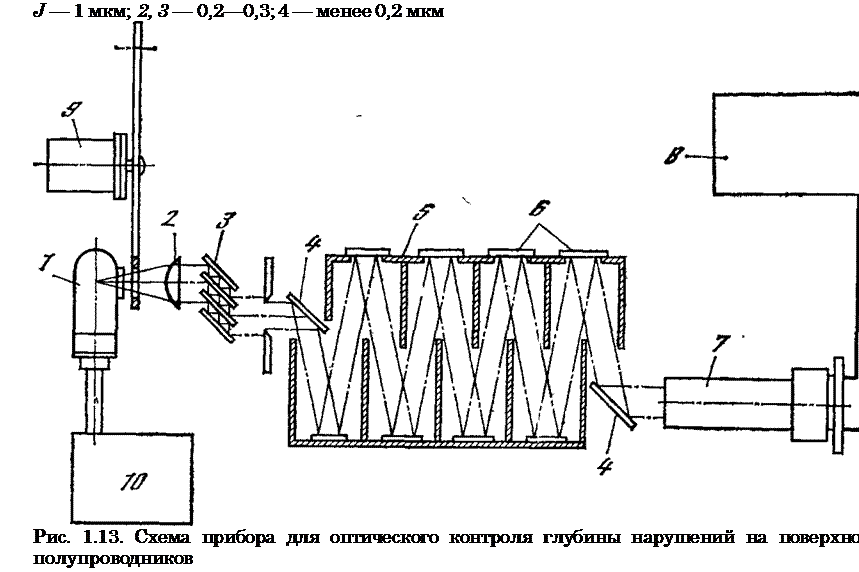Рис. 1.12. Спектральная зависимость коэффициента отражения арсенида галлия после обработки в полирующем травителе и при оставшихся нарушениях ловерхности на разной глубине

1 — водородная лампа; 2 — кварцевая линза; 3 — фильтр из пластин кремния, обрабо­танных окисью хрома; 4—плоские зеркала; 5 — корпус прибора с разделительными шторками; 6 — исследуемые пластины; 7 — фотоумножитель типа ФЭУ-57 или ФЭУ-39 с кварцевым входным окном; 8 — блок регистрации фототока; 9 — модулятор; ю — блок питания водородной лампы
нием поверхности кремния лучше вести при длине волны 0,28 мкм, где коэффициент отражения хорошо отполированного кремния до­стигает 70%. Для увеличения различия между коэффициентами от­ражения пластин с разной обработкой поверхности полезно восполь­зоваться прибором для наблюдения многократного отражения уль­трафиолетового излучения от набора пластин с одинаковой обра­боткой поверхности (рис. 1.13) [59]. В этом же приборе другой набор хорошо отполированных пластин позволяет выделить из спек­тра источника ультрафиолетовое излучение с длиной волны 0,28 мкм, наиболее полезное для контроля состояния поверхности кремния.

Приборы, применявшиеся для контроля состояния поверхности, в которых выделение необходимого спектрального интервала осу­ществлялось с помощью кварцевых призм, дифракционных решеток, параболических и поворотных зеркал, более сложны по конструкция.

* * *

Таким образом, исследования спектров отражения как в ультра­фиолетовой, так и в инфракрасной области дают возможность полу­чить информацию об электрофизических и оптических свойствах кристаллов, в частности помогают оценить концентрацию свободных носителей заряда, качество обработки поверхности, степень отжига дефектов, параметры зонной структуры, в том числе ширину за­прещенной зоны полупроводника и ее температурную зависимость.

Если отражение полупроводников в области основной полосы по­глощения практически не зависит от степени легирования приме­сями, ионизирующимися при комнатной температуре, то в длинно­волновой области спектра наблюдается резкий рост коэффициента отражения с увеличением количества таких примесей и, следователь­но, концентрации свободных носителей в полупроводнике.

Отражение в инфракрасной области спектра

Взаимодействие излучения со свободными носителями тока можно ‘ рассматривать в рамках классической электромагнитной теории из­лучения [25, 32], приводящей к результатам, весьма близким к по­лученным квантовомеханической теорией дисперсии [33].

Теория и эксперимент. Диэлектрическая постоянная полупровод­ника, равная квадрату его комплексного показателя преломления в i = (n—iky, (1.6)

определяется концентрацией N и эффективной массой т* носителей заряда, зарядом электрона q и круговой частотой падающей вол­ны со [25].

Раскрывая левую и правую части соотношения (1.6) и учитывая связь оптических и электрических свойств кристаллов, получим

п2—к2=е і,

2пк==Апа/(д,

где а —проводимость; п и к — показатели преломления и поглоще­ния полупроводника.

Анализ процесса электропроводности в переменном поле высо­кой частоты [32] приводит к следующим выражениям для прово­димости о и диэлектрической постоянной вещества Єї:

0=Ад2/™*<т/(1+ш2т2)>, (1.8)

*

Єі=8о—4яХс (1-9)

при этом поляризуемость, усредненная по всем Бременам релакса­ции т и энергия^ свободных носителей, определяется выражением

%-_Nq2Im*< т7(1+(оЧ2)>. (1.10)

Если частота падающего излучения много больше величины 1/т и <от>1, то поляризуемость %с не зависит от т и может быть опре­делена как

Хс ~ —Nq2/пг*ы2. (1.11)

Соотношения (1.6) — (1.11) впервые были использованы для оп­ределения эффективной массы носителей заряда оптическим мето­дом [34]. Для определения концентрации носителей заряда исполь­зовался эффект Холла. Был исследован также спектральный ход показателей поглощения и преломления в инфракрасной области для сильнолегированного германия. Из полученных данных видно, что слагаемым к2 при расчете коэффициента отражения г (см. форму­лу (1.4)) можно пренебречь вплоть до длин волн порядка 15 мкм, причем это справедливо также и для других полупроводников, ис­пользуемых для создания солнечных элементов.

С увеличением длины волны растет поляризуемость %с, подчи­няющаяся соотношению (1.11), и уменьшается диэлектрическая по­стоянная в соответствии с (1.9). При достаточно большом значении Хс диэлектрическая постоянная может стремиться к нулю. Частота, при которой наступает это явление, получила название собственной частоты плазменных колебаний сор, и может быть рассчитана из сле­дующего условия [32]:

е0=4я | Хс | =4 TcNq2/m*(op2, из которого легко получить соотношение

о)Р= (AnNq2/m*Bo)Ча

и, следовательно,

ХР= (яе 0c2m*/Nq2) v% где с — скорость света.

Явление плазменного резонанса происходит в области длин волн, где к2 мало и п также уменьшается, поскольку его изменение но-

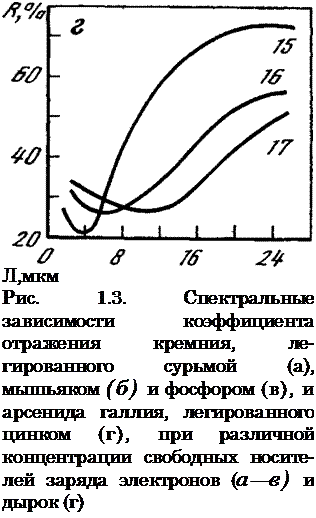
10 — 1,02* 1020;

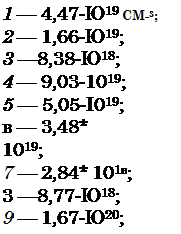
Л — 4,38* 10і9;

12 — 2,05 *1019;

13 — 1,27 1019;

14 — 7,4-І018;

15 — 1,5-1020;

16 — 3,2 10«;

17 — 1,7-101Э см-3 вторяет спектральный ход е4 в соответствии с выражением (1.7). Коэффициент однократного отражения г, определяемый по формуле (1.4), при малом значении к и 1 достигает минимального зна­чения rmin, характеризующего на кривой спектрального отражения область плазменного резонанса.

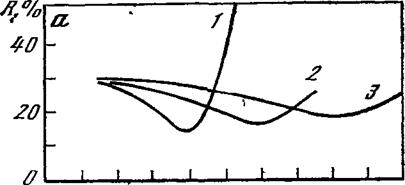
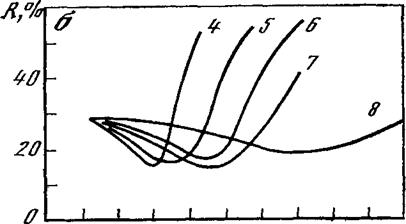
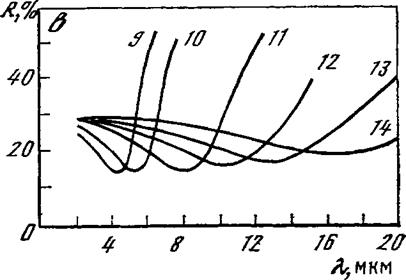
Спектральные зависимости коэффициента отражения кремния, легированного сурьмой, мышьяком и фосфором, с концентрацией свободных носителей заряда (электронов) от 7,4 -1018 до 1,67 — •1020 см“3 [35], и арсенида галлия, легированного цинком, с кон­центрацией свободных носителей заряда (дырок) от 3,2* 1019 до 1,5* 1020 см”3 [36], представлены на рис. 1.3, где хорошо видны по­ложение минимума плазменного резонанса на спектральных кривых отражения от поверхности кремния и арсенида галлия и зависи­мость длины волны минимального отражения от концентрации сво­бодных носителей.

Значение Гшт определяется показателем поглощения Лс, так как при 1 коэффициент г тем меньше, чем меньше к (что видно из соотношения (1.4)). В свою очередь показатель поглощения зави­сит от времени релаксации, поскольку Оно влияет на проводимость. В то же время поляризуемость не зависит от т, а определяется зон­ной структурой и концентрацией свободных носителей.

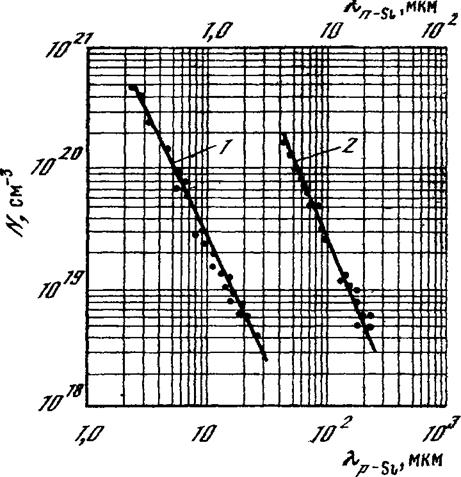
Рис. 1.4. Зависимости концентра* ции свободных носителей заряда от длины волны плазменного минимума для p-Si (1) и n-Si (2)

Точки — эксперимент

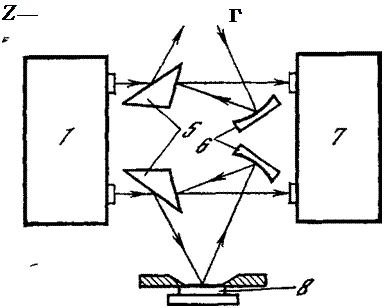
Рис 1.5. Ход лучей в спектрофо­тометрах ИКС-14 (а) и «Хитачи» (б) с приставками для измере­ния отражения

1 — источник излучения;

2 — держатель образцов;

3 — образец;

4 — малогабаритный термостат;

5 — плоские зеркала;

6 — вогнутое зеркало;

7 — монохроматор и приемник

излучения;

8 — эталонное алюминиевое зеркало

т

Поглощение света свободными носителями увеличивается с рос­том длины волны, а повышение к приводит к возрастанию коэффи­циента отражения. Таким образом, спектральная зависимость коэффициента отражения легированных полупроводников проходит через минимум, что и было получено в эксперименте (см. рис. 1.3). Поляризуемость пропорциональна произведению NX С увеличени­ем концентрации свободных носителей N то же значение поляри­зуемости (в частности, |хс|, при котором 1) может достигаться при меньших X. Именно поэтому при повышении концентрации сво­бодных носителей спектральное положение Гщщ сдвигается в корот­коволновую область, причем значение rm in при этом уменьшается, поскольку падает к.

Эта особенность спектров отражения легированных полупровод­ников в инфракрасной области может быть положена в основу про­стого оптического метода определения концентрации носителей N
из спектров отражения. Зависимости спектрального положения дли­ны волны плазменного минимума для электронного сильнолегирован — ного кремния гс-типа (Xn-si) и дырочного p-типа (XP-si) от концен­трации носителей (рис. 1.4) выражаются^аналитически в виде двух следующих соотношений [37]:

iVP=3,27 • 1021 Vsr2’11, iVn=6,29-1021 К-*Г2’*

хорошо аппроксимирующих экспериментальные данные. При этом концентрация носителей в эталонных образцах определялась по из­мерению слоевого сопротивления четырехзондовым методом с ис­пользованием кривых Ирвина, связывающих удельное сопротивление р — и и-кремния с концентрацией свободных носителей [31, 38]. Не­достатком данного метода является сравнительно невысокая точ­ность установления спектрального положения длины волны плаз­менного минимума для слаболегированных образцов.

Более сложные и точные методики определения концентрации подвижности и эффективной массы свободных носителей заряда по спектрам отражения легированных полупроводников описаны в ра­ботах [39—42]. В некоторых из них измеренные зависимости отра­жения сравниваются с эталонными кривыми в весьма широком спектральном диапазоне — от 1 до 25 мкм.

Исследование* спектров отражения от поверхности полупровод­ников дает возможность получить информацию не только об элек­трофизических свойствах кристаллов, но и о состоянии их поверх­ности, качестве химической и механической обработки. Это удается сделать, несмотря на то что из-за трудностей регистрации суммар­ного и диффузного отражения в инфракрасной области [43] изме­ряется, как правило, лишь зеркальная составляющая коэффициента отражения и ее температурная зависимость [44].

Методика измерений. Для измерения коэффициента отражения используется инфракрасный спектрофотометр, например отечест­венный марки ИКС-14 (диапазон спектра от 0,7 до 25 мкм), или японский марки «Хитачи» (измеряемый диапазон спектра от 2 до 50 мкм). Оба спектрофотометра в основном применяются для из­мерения коэффициента пропускания, а для измерения коэффициента отражения необходима установка специальных приставок [41, 45] между источником и приемником излучения (рис. 1.5).

Для проведения таких измерений удобна конструкция описан­ных в статье [44] держателя для образцов и малогабаритного тер­мостата. Электрическая схема последнего основана на релейном принципе и может поддерживать любую заданную температуру в интервале 30—300° С с точностью ±2° С.

Измерения фонового теплового излучения исследуемых образцов показали, что даже в далекой инфракрасной области фоновое из­лучение при 200° С не превышает 14% от отраженного потока [44]. Фоновое излучение нагретого эталонного зеркала составляет ме­нее 1% благодаря малой степени черноты пленок алюминия [46].

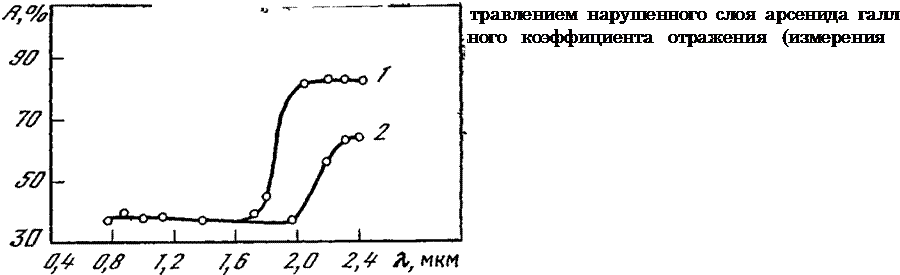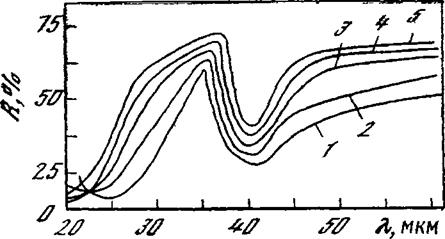
Рис. 1.6. Зависимость коэффи­циента отражения механически шлифованной поверхности арсе­нида галлия л-типа в инфракрас­ной области спектра до (1) и пос­ле удаления травлением внешне­го слоя (2—5) различной тол­щины

Si—S5 — площади, ограниченные кривыми 1—5 на рис. 1 6

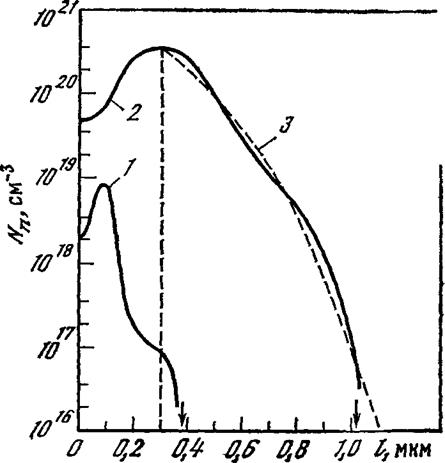Рис. 1.9. Зависимость концентрации свободных носителей заряда в по­верхностном легированном слое кремния, полученном бомбардиров­кой кремния p-типа ионами фосфо­ра, от расстояния до поверхности

1 — до отжига, доза ионов фосфора

6 103 мкКл/см2;

2 — тот же образец после отжига

в течение 2 ч при 850° С;

3 — теоретическая кривая,

соответствующая диффузии примеси из бесконечного источника, расположенного на расстоянии 0,3 мкм от поверхности Стрелки указывают глубину залегания р—п-перехода

Оценка качества механической обработки поверхности полупро­водников. Измерения спектров инфракрасного отражения при ком­натной температуре, выполненные с помощью инфракрасных спек­трофотометров, дают возможность оценить степень повреждений поверхности полупроводников при механической обработке, напри­мер, как это было сделано для арсенида галлия /г-типа [47] (ко­нечно, для успешного осуществления подобного контроля необхо­димо, чтобы длина волны падающего излучения была соизмерима с глубиной нарушений йа поверхности). При этом контролировались сравнительно грубые нарушения, вызванные механической шлифов­кой абразивом со средним диаметром зерна около 10 мкм, и для исследования был выбран диапазон спектра от 20 до 60 мкм.

В этой области на кривой отражения легированного арсенида галлия (рис. 1.6) наблюдаются два характерных минимума: при 20— 25 мкм (вызванный явлением плазменного резонанса излучения со свободными носителями заряда) и при 37—42 мкм (связанный с поглощением излучения из-за взаимодействия с тепловыми колеба­ниями решетки кристалла). После удаления слоя определенной тол­щины спектральная зависимость коэффициента отражения остается неизменной и совпадает с аналогичной зависимостью ненарушенно­го кристалла арсенида галлия /г-типа с такой же концентрацией примеси. Для удаления нарушенного слоя использовался травитель, состоявший из смеси серной кислоты, перекиси водорода и воды, а толщина удаляемого слоя определялась взвешиванием образцов до и после травления. Достаточно точно глубину нарушенного слоя на поверхности кристалла можно определить по зависимости пло­щади, ограниченной кривой спектрального коэффициента отраже­ния, от толщины удаленного чслоя (рис. 1.7). Площадь под кривой спектрального коэффициента отражения перестала возрастать после удаления нарушенного слоя глубиной 8,8 мкм. Глубина нарушений тем самым составляет около 0,9 от среднего диаметра абразивного зерна, использованного для механической шлифовки поверхности ар­сенида галлия.

Оценка температурной зависимости ширины запрещенной зоны. Использование малогабаритного термостата [44] дает возможность исследовать температурную зависимость коэффициента зеркального отражения от поверхности образцов, оценить изменение ширины за­прещенной зоны полупроводников при росте температуры. Показан­ное на рис. 1.8 изменение спектрального отражения от внешней по­верхности пластинки поликрист ал л ического германия р-типа с удельным сопротивлением 60 Ом-см и нанесенным на ее тыльную сторону отражающим слоем алюминия (испарением в высоком ва­кууме) [44] обусловлено температурным сдвигом края основной по­лосы поглощения германия.

Исследование свойств тонких сильнолегированных слоев полу­проводников с помощью спектров отражения инфракрасного излу­чения не может привести к количественным результатам, когда глу-

бина проникновения излучения в материал полупроводника превы­шает толщину слоев. Это положение подтверждается при исследо­вании тонких р—тг-переходов, полученных бомбардировкой кремния ионами фосфора [48]. Методики, использованные в этих эксперимен­тах, являются примером комплексного подхода к изучению свойств полупроводниковых структур. Были определены профиль концен­трации свободных носителей заряда, глубина залегания р—п-пере — * хода и их изменение в процессе изотермического отжига.

Исследование тонких легированных слоев в солнечных элементах. В экспериментах использовался кремний p-типа с удельным сопро­тивлением р=1 Ом-см. Тщательно полированная поверхность, ори­ентированная по {1Н}, подвергалась бомбардировке сепарирован­ным пучком ионов фосфора с энергией 30 кэВ дозой D=6-103 мкКл/ /см2. Профиль концентрации свободных носителей тока исследовался при последовательном удалении слоев кремния толщиной 160— 500 А анодным окислением в 0,04 N растворе азотнокислого калия в этиленгликоле [49]. Проводимость удаляемых слоев измерялась четырехзондовым методом. Пересчет к средней концентрации сво­бодных носителей в удаленном слое велся с использованием данных работ [38, 50]. Общая глубина легированного слоя оценивалась по методу косого цилиндрического шлифа [51].

Коэффициенты пропускания и отражения в области спектра 1— 25 мкм определялись с помощью спектрофотометра ИКС-14 с ис­пользованием приставки для измерения коэффициента зеркального отражения (см. рис. 1.5, а).

Результаты электрических измерений. На рис. 1.9 (кривая 1) представлено распределение концентрации свободных носителей по глубине легированного слоя. У поверхности образуется относитель­но широкая область с отрицательным градиентом концентрации, максимум достигается на глубине около 0,12 мкм, после чего кон­центрация уменьшается до значения, соответствующего исходному кремнию. Ход кривой объясняется специфичностью профиля кон­центрации внедренных атомов [52] и радиационных дефектов: мак­симум концентрации сдвинут к поверхности [53—55]. Проведенные электронографические исследования поверхности кремния, подверг­нутой бомбардировке ионами фосфора, обнаружили аморфизацию кремния вплоть до глубины 0,2 мкм, причем верхний слой толщи­ной 0,05 мкм из монокристаллического состояния перешел пол­ностью в аморфное [48]. Количественная оценка средней по слою концентрации носителей тока (см. кривую 1 на рис. 1.9) дает зна­чение порядка 1018 см~3, что примерно в 1000 раз меньше средней концентрации введенного фосфора (3-Ю21 см“3).

Уменьшение количества радиационных дефектов и увеличение концентрации электрически активных внедренных атомов фосфора, как известно, легко достигаются тепловым отжигом образцов (см. рис. 1,9, кривая 2). Глубина залегания р—тг-перехода увеличилась до 1 мкм. Участок кривой 2 от 0,3 до 1 мкм довольно хорошо они-

-сывается уравнением диффузии примеси из бесконечного источни­ка в полу ограниченное тело [56]. Интегрирование кривой 2 пока­зало, что в кремний из начального слоя толщиной 0,3 мкм продиф- фундировало 4,2% фосфора. По мере приближения к поверхности, так же как и до отжига, наблюдается уменьшение концентрации — свободных носителей тока. Электронограммы, полученные при по­следовательном удалении слоев, показали остаточные нарушения

Рис 1.10. Зависимость коэффи-

7/7

циента отражения кремния, /и легированного ионной бомбар­дировкой фосфором, при дли­не волны 19 мкм от темпера — ^ туры отжига

— 30

о т 7оо зоо % °с

монокристалличности до глубины 0,15 мкм, что подтверждает не­полноту отжига, вследствие чего концентрация свободных носите­лей в этом слое не могла стать высокой.

Результаты оптических измерений. Была сделана попытка ис­следовать распределение концентрации свободных носителей в ле­гированном слое по изменению коэффициента отражения в инфра­красной области спектра. Коэффициент отражения образцов, не под­вергнутых отжигу после ионной бомбардировки, совпадает с коэф­фициентом отражения нелегированного кремния. В этом случае по­верхностная концентрация свободных носителей iV^lO18 см”3, однако глубина залегания перехода настолько мала (0,2—0,3 мкм), что ле­гированный слой оказывается в высокой степени прозрачным в окрестности Х—19 мкм. Это говорит о том, что для мелких р—п — переходов (глубина залегания <1 мкм) изменение коэффициента отражения при послойном снятии кремния не передает истинного распределения концентрации свободных носителей в легированном слое, так как значение коэффициента отражения обусловливается не только поверхностными, но и всеми нижележащими слоями с умень­

Тем не менее проведенные измерения коэффициента отражения полезны. Например, они показывают, что при одинаковой глубине залегания перехода концентрация свободных носителей после тепло­вого отжига выше при наличии пленки двуокиси кремния, препят­ствующей экзодиффузии фосфора.

Кроме того, по значению коэффициента отражения в инфракрас­ной области спектра можно судить о полноте отжига при выбран­ных условиях. На рис. 1.10 показано изменение коэффициента от­ражения при Я=19 мкм легированной ионной бомбардировкой фос­фором (по описанному выше режиму) поверхности кремния после отжига в течение 2 ч при возрастании температуры отжига от 600 до 890° С. Чем выше концентрация свободных носителей в поверх­ностных слоях легированной области, тем больше коэффициент от­ражения: i?=30% при 7Vp=1016 см~3 и R—84% при Л^п=2,5-1020см~3.

В квантовой механике элементарные частицы, в том числе и элек­трон, рассматриваются одновременно и как волны. В связи с этим при описании движения элементарных частиц используются не толь­ко такие величины, как энергия Е и импульс р, но и, например, длина волны Л, частота v и волновой вектор к=р/Л, где Л —постоян­ная Планка. При этом E=hv и p=h/X. Зонную структуру кристалла часто представляют в виде диаграммы Е—к, используя при этом обычно значения энергии в электронвольтах, а волнового векто­ра к —в долях постоянной решетки кристалла, причем на оси к с помощью стрелок указываются направления кристаллографиче­ской ориентации, что позволяет достаточно полно отразить измене­ние зонной структуры в объеме кристалла.

Вид зависимости Е—к помогает понять также характер межзон­ных переходов в данном полупроводниковом веществе и, в частно­сти, определить, являются они «прямыми» или «непрямыми» [10]. Если минимум зоны проводимости и максимум валентной зоны сов­падают в k-пространстве, то переброс электрона через запрещенную зону за счет оптического или теплового возбуждения происходит вертикально, без изменения волнового вектора. Такие переходы на­зываются прямыми. Если же экстремумы зон не совпадают и тре­буется изменение к, то в процессе переброса электрона должен участвовать посредник, например квант колебаний решетки — фонон или ион примеси, которые передадут электрону часть своей энер­гии. Подобные переходы получили название непрямых.

У многих полупроводников в силу сложного строения энергети­ческих зон поглощение излучения носит смешанный характер: на­чавшись с непрямых переходов (в этом случае для переброса элек­трона — требуется меньше энергии и первоначально поглощаются фо­тоны небольших энергий), процесс поглощения при больших энер­гиях происходит уже исключительно за счет прямых переходов.

Следует отметить также, что’ значение ширины запрещенной зоны, определенное при измерениях оптического поглощения, зависит в значительной степени от концентрации свободных носителей заряда в полупроводнике, температуры и наличия в запрещенной зоне при­месных уровней. Если состояния вблизи дна зоны проводимости и потолка валентной зоны заполнены носителями заряда, то оптиче­ские измерения дадут для ширины запрещенной зоны примесного полупроводника значения более высокие, чем для чистого собствен­ного полупроводника. Если примесная зона слилась с краем бли­жайшей разрешенной зоны, что может произойти при сильном ле­гировании, то ширина запрещенной зоны уменьшится. Сужение Её заметно скажется на положении края основной полосы поглощения {он сдвинется в длинноволновую область).

Коэффициент поглощения полупроводника а определяется усло­вием, что энергия волны уменьшается в е раз на расстоянии, рав­
ном 1/а:

Ni=N0exp (—аZ),

где iV| — плотность потока прошедших в полупроводник фотонов на глубине I; N0 — плотность потока фотонов, пересекших поверхность полупроводника (после отражения части света от поверхности).

В области спектра, где величина аI относительно мала и часть света проходит через полупроводник, расчет суммарного коэффи­циента пропускания Т необходимо вести с учетом многократных от­ражений внутри полупроводниковой пластинки по следующей фор­муле [25]:

гр __ (1 — г)2 exp ( — al)

1 — г2 ехр (— 2аI)

Здесь коэффициент однократного отражения от поверхности по­лупроводника (когда обе поверхности — внешняя и тыльная — в он— тическом смысле идентичны)

(п — 1)2+ к2

г (п + 1 )2—j— А? »

где п и к — показатели соответственно преломления и поглощения: полупроводникового материала.

Суммарный коэффициент отражения R [23] от такой пластинки (с учетом многократных отражений в ней) в общем случае (когда коэффициенты однократного отражения от внешней и тыльной по­верхностей не одинаковы) может быть определен по формуле

я — Г 4- (! + Гр)2 г2 ехр (— 2а/)

0 ‘ 1 — г0г2 ехр (— 2aZ) ’

где г0 — коэффициент однократного отражения от внешней поверх­ности (граница воздух—полупроводник); г2 — коэффициент одно­кратного отражения от тыльной поверхности (граница полупровод­ник-воздух) .

Коэффициент поглощения а материала связан с его показателем поглощения к следующим соотношением [25]:

а=4 пк/К. (1.5)

Таким образом, измеряя интенсивность оптического излучения, прошедшего через полупроводниковые образцы различной точно из­меренной толщины, можно определить значения к и а данного ве­щества. При анализе результатов этих измерений следует помнить об отражении излучения внутри полупроводника от обеих границ раздела исследуемых пластин и об оптических потерях на внешней и тыльной поверхностях пластин. Корректные измерения, при ис­пользовании результатов которых расчет значительно упрощается и уточняется, требуют, чтобы у образцов различной толщины вы­сокое качество обработки обеих поверхностей (и, следовательно, коэффициенты отражения — и пропускания) было одинаковым, а эф­фекты интерференции отсутствовали.

В спектральной области, где к мал, показатель преломления п лиожет быть найден по формулам Френеля при использовании из­меренного значения коэффициента отражения от одной из поверх­ностей полупроводниковой пластины на границе с воздухом. Отра­жение от второй, тыльной поверхности лучше при измерениях ис­ключить каким-либо экспериментальным приемом, например грубой шлифовкой этой поверхности или полировкой под углом.

Солнечные элементы в большинстве случаев представляют со­бой полупроводниковую пластину двухслойной структуры: на срав­нительно толстом слаболегированном базовом слое, например из кремния, находится сильнолегированный внешний кремниевый слой (наиболее простая модель элемента).

В ходе расчета оптических свойств таких двухслойных структур [23] проводится усреднение коэффициента отражения по фазовому углу, или, иначе, фазовой толщине слоев (ибо при толщине слоев, .значительно превышающей длину волны, значение фазовой толщи­ны становится недопустимо большим и сильно зависящим от незна­чительных изменений толщины слоев и длины волны, что не соот­ветствует реальной физической картине). Формула для коэффици­ента пропускания Т такой двухслойной структуры после усреднения выглядит следующим образом:

т I Ы21 к |2 ехр (— кл гл4я/Х)

— 1 — | /о |а гг |2 ехр (— кл 1л8п/Х) ’

где go и /о — коэффициенты Френеля на границе воздух—сильноле­гированный кремний; ti и г і — амплитудные коэффициенты пропус­кания и отражения на границе сильнолегированный кремний—базо­вый слой кремния; кл и 1Л — соответственно показатель поглощения и толщина сильнолегированного слоя кремния.

Зная оптические константы обоих слоев кремния и измерив оп­тическое пропускание двухслойной пластины кремния, можно опре­делить толщину сильно легированного слоя (конечно, в предполо­жении, что оба слоя кремния легированы равномерно). Коэффициент пропускания двухслойной структуры при прозрачном базовом слое, что справедливо для длинноволновой спектральной области за кра­ем основной полосы поглощения кремния, заметно зависит от тол­щины сильнолегированного слоя (см. в работе [23] рис. 1.5).

Определение оптических констант сильнолегированного слоя кремния (как и других полупроводниковых материалов), что явля­ется методически наиболее сложной задачей, может быть выполнено при использовании методики, предложенной в статье [26]. Для практического осуществления этой методики необходимо иметь набор эталонных образцов исследуемого полупроводникового материала с известной концентрацией свободных носителей и измерить спек­тральную зависимость коэффициента отражения. Для кремния с концентрацией носителей от 2,2-1018 до 11,5-1019 см-3 такие эталон­ные кривые были получены в работе [26]. Дальнейший расчет тре —

тельной части е0 диэлектриче­ской ПОСТОЯННОЙ Єї. Для чисто­го собственного кремния Єо=

= 11,67 [27]. Значение диэлект­рической постоянной Єї опре­деляется по спектральной за­висимости коэффициента отра­жения Я (Я) путем графической экстраполяции, затем рассчиты­ваются пик [26].

Таким образом, оптические методы исследования дают воз­можность определить геометри­ческие толщины полупроводни­ковых слоев, участвующих в процессе поглощения света, оп­тические константы п и к и их

✓

спектральную зависимость, а также и спектральную зависи­мость коэффициента поглоще­ния а полупроводникового материала (см. соотношение (1.5)).

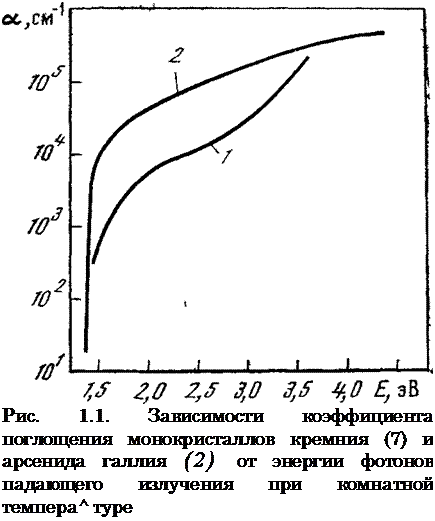
На рис. 1.1 представлены зависимости коэффициента поглоще­ния а от энергии фотонов падающего излучения двух наиболее часто используемых в полупроводниковой фотоэнергетике материалов — кремния [28] и арсенида галлия [29, 30]. Именно из этих мате­риалов получены наиболее эффективные современные солнечные элементы. На рис. 1.1, как и далее в книге, если не сделано особой

щенной зоны арсенида галлия, и коэффициент поглощения а быстро достигает значений 104—105 см”1. Поглощение в кремнии (в ос­новной полосе) начинается с непрямых переходов при 1,1 эВ с уча­стием фононов, коэффициент поглощения растет сравнительно мед­ленно (до значений 103—104 см-1). Только при энергии фотонон около 2,5 эВ переходы зона—зона становятся прямыми — поглоще­ние резко возрастает.

Для германия также характерны непрямые оптические переходы* начинающиеся при 0,62 эВ (коэффициент поглощения от 1 до Ю2 см-1), и только при энергии фотонов более 0,81 эВ основноа поглощение определяется прямыми переходами [27].

Следует отметить, нто значение термической ширины запрещен­ной зоны полупроводника, рассчитываемое по рассмотренной выше температурной зависимости электропроводности, совпадает, как пра­вило, со значением оптической ширины запрещенной зоны, опре­деляемым краем основной полосы поглощения, совпадающим с на­чалом непрямых оптических переходов зона—зона»

Спектральные зависимости коэффициента поглощения (см. рис. 1.1) показывают, что, применяя кремний, можно использовать для преобразования в электрический ток большую часть солнечного спектра (излучение с длиной волны 1,1 мкм и короче), т, е. более 74% энергии внеатмосферного солнечного излучения. Для арсенида таллия фотоактивным (способным перебросить электроны через за­прещенную зону) является излучение с длиной волны 0,9 мкм и менее, и в силу только этого ограничения лишь 63% энергии Солн­ца во внеатмосферных условиях может быть преобразовано в элек­трическую. Однако из-за непрямых оптических переходов и малых значений коэффициента поглощения в области края основной поло­сы поглощения толщина кремниевого солнечного элемента, погло­щающего все фотоактивное излучение, должна быть не менее 250 мкм, в то время как аналогичная толщина солнечного элемента из арсенида галлия может составлять не более 2—5 мкм. Эту осо­бенность спектральных характеристик поглощения необходимо учи­тывать при разработке высокоэффективных и дешевых тонкопле­ночных солнечных элементов.

Если энергия фотонов падающего излучения настолько мала, что они не могут перебросить электроны из валентной зоны в зону про­водимости, то под воздействием излучения электроны могут совер­шать переходы внутри разрешенных зон. Это отразится на спектре поглощения в длинноволновой области непосредственно за краем основной полосы поглощения полупроводника. Данный вид погло­щения, получивший название поглощения свободными носителями, проявляется тем сильнее, чем выше концентрация ионизированных примесей и, следовательно, свободных носителей заряда в полупро­водниках, а также чем больше количество свободных носителей, инжектированных в полупроводник под действием света или элек­трического тока.

Изучение спектров поглощения длинноволнового излучения в полупроводниках привело к обнаружению еще нескольких харак­терных видов поглощения: на колебаниях решетки; примесного; эк — чжгонного, связанного с возбуждением пары электрон—дырка, одна­ко не влияющего на концентрацию свободных носителей заряда, в силу того что по кристаллу в э1ч)м случае движется возбужденное состояние, а не отдельно электрон и дырка.

Экспериментальные кривые для легированного кремния, представ­ленные на рис. 1.2, подтверждают зависимость коэффициента по­глощения в инфракрасной области спектра от концентрации свобод­ных носителей заряда [И].

Спектры поглощения дают обширную и полезную информацию о структурных особенностях кристалла, о степени его легирования, позволяют определить энергию активации примесей и, следователь­но, положение занимаемых ими в запрещенной зоне энергетических уровней. С помощью спектров поглощения удается исследовать даже

Рис. 1.2. Зависимость коэффициен — та поглощения кремния, легирован­ного бором по разной концентрации, от энергии фотонов (измерения Про — /О3 ведены при температуре 300 К)

1— 3 — соответственно 6 І019, 9,7 «Ю19 и

2 Ю20 СМ-3

2

2 70

столь тонкий эффект, как присутствие в кремнии растворенного кис­лорода (благодаря характерной для него полосе поглощения при 9 мкм), и определить концентрацию кислорода в кремнии [31].

При образовании твердого тела, например кристалла полупровод­ника, атомы настолько сближаются друг с другом, что их внешние электронные оболочки перекрываются. Вместо индивидуальных ор­бит отдельных атомов появляются коллективные орбиты, и подобо­лочки атомов объединяются в зоны, единые для всего кристалла*. Характер движения электронов при этом изменяется кардиналь­ным образом: электроны, находящиеся на определенном энергетиче­ском уровне одного атома, получают возможность без затраты энер­гии переходить на подобный же уровень соседнего атома и тем самым свободно перемещаться вдоль всего кристалла.

Внутренние оболочки в изолированных атомах, а следовательно, и в кристаллах целиком заполнены. Самая же верхняя зона, обра­зованная из уровней, на которых располагались валентные элек­троны, не всегда заполнена до конца. Электропроводность кристал­лов, их оптические и многие другие свойства в основном определя­ются степенью заполнения валентной зоны и расстоянием от нее до самой верхней зоны, получившей название зоны проводимости. Электроны, попавшие из валентной зоны, например за счет тепло­вого или оптического возбуждения, в зону проводимости, могут при­нимать участие в переносе электрического тока. Перемещение элек­тронов на освободившиеся места в валентной зоне создает встреч­ное движение положительных зарядов, называемых дырками. Поло­жительный заряд всегда образуется в валентной зоне после ухода электрона, ведь до этого зона была электронейтральной.

Вещества, у которых валентная зона заполнена целиком, а рас­стояние до следующей зоны велико, называются диэлектриками. Для металлов характерно другое энергетическое строение: валент­ная зона заполнена частично либо перекрывается со следующей свободной зоной, зоной проводимости. Если же у вещества валент­ная зона заполнена целиком, но энергетическое расстояние до зоны проводимости мало (условно — менее 2 эВ), то такие вещества на­зывают полупроводниками. Электропроводность и другие свойства полупроводников сильно зависят от внешних условий, особенно от температуры Т. С повышением Т экспоненциально растет число теп­ловых перебросов электронов через запрещенную зону с энергети­ческой шириной Eg, разделяющую валентную зону и зону проводи­мости, увеличивается число электронов в зоне проводимости и дырок в валентной зоне, а электропроводность полупроводника а возраста­ет по закону

о^А0ехр (—EJ2KT), . (1.1)

где К — постоянная Больцмана; А0 — константа, характеризующая данное вещество.

Электропроводность металлов в силу постоянства концентрации свободных электронов определяется температурной зависимостью подвижности электронов и с ростом температуры медленно падает.

Если зависимость (1.1) прологарифмировать, то она примет сле­дующий вид:

In о = InAo—Eg/lKT. (1.2)

Зависимость (1.2) можно изобразить графически в так называе­мых полулогарифмических координатах и получить прямую, тангенс утла наклона которой <р позволяет рассчитать важнейший параметр полупроводника, определяющий его электрические и оптические свойства — ширину запрещенной зоны Eg:

tg у=Е/2К.

Следует отметить, что зависимость логарифма электропроводное сти от 1/Т представляет собой наклонную прямую линию лишь длЯ’

*

чистых, лишенных посторонних примесей полупроводников, полу­чивших название собственных. Легирующие примеси, вводимые в полупроводники, как правило, для придания им электронного или дырочного характера электропроводности, занимают энергетические уровни в запрещенной зоне вблизи дна зоны проводимости (доно­ры), легко отдающие электроны в зону проводимости при неболь­шом тепловом или оптическом возбуждении, или около потолка ва­лентной зоны (акцепторы), на которые легко забрасываются элек­троны из заполненной нижней зоны, вследствие чего в кристалле пдявляется исключительно дырочная проводимость, не сопровож­даемая движением электронов в верхней зоне.

Для примесных полупроводников зависимость In о от 1 /Т носит более сложный характер и состоит из отрезков двух наклонных прямых, соединенных горизонтальным участком. Тангенс угла на­клона отрезка прямой, лежащей в области низких температур, дает возможность определить энергию активации или энергетическое по­ложение примесных уровней в запрещенной зоне; тангенс утла на­клона отрезка прямой, расположенной в области высоких темпе­ратур, позволяет найти значение ширины запрещенной зоны Ег примесного полупроводника. Появление горизонтального участка объясняется постоянством концентрации электронов в зоне прово­димости (донорные уровни себя исчерпали) в определенном интер­вале средних температур.

Характер температурной зависимости полупроводников не может быть положен сейчас в основу четкого определения полупроводни­ков и их отличия от других веществ [11]. Теоретически и экспе­риментально изучены многочисленные случаи отклонения от ука­занных выше зависимостей. Так, в сильнолегированных полупровод­никах электропроводность с повышением температуры не растет, а слабо уменьшается, почти как у металлов. Обнаружены полупро­водниковые сверхпроводники, у которых электропроводность резко возрастает при приближении температуры к абсолютному нулю. Найден обширный класс полупроводников, в которых перенос за­ряда осуществляется ионами, а не электронами и электропровод­ность которых подчиняется совершенно иным закономерностям (та­ковы, например, стеклообразные полупроводники). В связи с этим в настоящее время правильнее определять полупроводники как класс веществ, свойства которых могут изменяться в очень широких пре­делах под действием различных внешних воздействий (температу­ры, освещения, давления, электрических и магнитных полей и др.)> Именно эта особенность полупроводников обусловила получение на их основе исключительно чувствительных фото — и термосопротивле­ний, электронных приборов, например диодов, транзисторов, тири­сторов, детекторов электрического и магнитного полей или радиа­ционных частиц, тензодатчиков и др., которые было бы невозможно создать из металлических или диэлектрических веществ.

М. М. КОЛТУН

Колтун М. М. Оптика и метрология солнечных элементов.— М.: Наука, 1985.— 280 с.

f

Представлены оптические и электрические характеристики солнечных элементов и батарей из различных полупроводниковых материалов. Рас­сматриваются способы градуировки эталонных солнечных элементов, раз­работанные методики измерений КПД, применяемые к наземным и вне­атмосферным условиям, конструкции имитаторов солнечного излучения, пути повышения эффективности и улучшения оптических свойств фото­электрических преобразователей солнечной энергии, в частности, с по­мощью просветляющих покрытий

Для специалистов в области солнечной энергетики, оптики и метро­логии полупроводниковых приборов Табл 10. Ил. 112 Библиогр. 494 назв.

Рецензенты В. А рилихес, Б. В. Тарнижевсюш

t

К проблеме освоения энергии солнечного света привлечено в на­стоящее время внимание специалистов разных научных дисциплин — от химии и биологии до физики твердого тела [1]. Особенно боль­шие успехи достигнуты на пути создания полупроводниковых сол­нечных элементов и батарей различных конструкций [2]. Все круп­нее, легче и мощнее становятся солнечные батареи космических ап­паратов и станций [3], все шире их применение на земле [4], все выше КПД и разнообразнее их свойства [5].

Около тридцати лет прошло с момента проведения первых работ, положивших начало современной фотоэлектрической энергетике [6, 7] (краткая справка научной и практической значимости их дана в статьях [8, 8а, 86]). Эти исследования, в сваю очередь, опирались на стройную теорию фотоэлектрических явлений в полупроводни­ках, созданную в 30—40-е годы нашего столетия. В СССР развитие этого направления физики полупроводников определили работы ака­демика А. Ф. Иоффе и его школы, углубившие наше понимание природы фотопроводимости и фотоэлектрических явлений в полу­проводниках и полупроводниковых р—^-переходах [9—12]. Резуль­таты отечественных и зарубежных исследований в области создания фотоэлектрических приборов, преобразующих энергию излучения, в том числе солнечного, в электрическую, были полно и всесторон­не обобщены в монографиях [12, 13]. Полезные теоретические и ^практические рекомендации по выбору оптимальной конструкции фотопреобразователей и описание их электрофизических характе­ристик даны в публикациях [14—19]. Создание надежных и легких конструкций солнечных батарей (в основном космического назна­чения) и вопросы воздействия на них космического излучения рас­смотрены в обзорах [20—22], исследования по разработке оптималь­ных просветляющих, теплорегулирующих и радиационно-защитных оптических покрытий для солнечных элементов и батарей представ­лены в книге [23].

Настоящая монография посвящена проблемам оптики и метро­логии солнечных элементов и является первой в этой области. Сло­ва «оптика» и «метрология» недаром стоят рядом в названии книги. Только знание комплекса оптических и метрологических характе­ристик солнечного излучения и имитаторов Солнца, а также полу­проводниковых солнечных элементов и применение разнооб­разных способов эталонирования численных значений параметров элементов позволяют квалифицированно оценить эффективность по­следних и наметить дальнейшие пути увеличения их КПД. Нет другого способа оценки качества преобразователей солнечной энер-

гии (в том числе — качества солнечных элементов), чем измерение, основанное на разумной, проверенной методике. Недаром известный оптик С. Толанский отмечал, что веками освященную формулу: уви­деть значит поверить, нельзя считать верной в наше время [24]. Сегодня поверить можно только после точного измерения.

Автор выражает глубокую признательность ответственному ре­дактору книги, научным работникам различных организаций нашей страны, коллегам, сотрудникам и аспирантам (результаты совмест­ных исследований с ними легли в основу многих разделов настоя­щей книги). Большое всестороннее участие в подготовке рукописи к печати принимали Г. А. Гухман, И. В. Грачева и Т. Н. Федоров­ская, которым автор искренне благодарен.

Созданию солнечных элементов предшествовали детальное изучениа оптических свойств полупроводников, исследование процессов вза — имодействия света с веществом внутри полупроводникового мате­риала, приводящих к появлению избыточных, неравновесных носи­телей заряда.

Для понимания оптических и фотоэлектрических свойств солнеч­ных элементов необходимо хотя бы кратко рассмотреть качествен­ные особенности зонной структуры полупроводников, ее отличие от электронного строения металлов и изоляторов, основные оптические характеристики полупроводниковых веществ, определяемые зонной структурой, и уже затем перейти к анализу оптических и фото­электрических свойств самих солнечных элементов (и, конечно, ме­тодов их измерения), а также методов определения и исследования структурных и электрофизических параметров отдельных полупро­водниковых слоев элементов. Эти параметры в значительной степе­ни определяют как характеристики, так и эффективность солнечных: элементов и батарей.

В первой главе, как и в целом в книге, не будут затрагиваться проблемы, связанные с концентрацией солнечного излучения, по­ступающего на поверхность солнечных элементов, и разработкой светоделительных устройств, изменяющих его спектральный состав. Обе эти проблемы достаточно полно освещены в специализирован­ной литературе.