J. Dersch1*, K. Hennecke1 and V. Quaschning2

1 DLR — German Aerospace Center, Linder Hohe, 51147 Koln, Germany
2 FHTW Berlin, Berlin University of Applied Sciences, Marktstrasse 9, 10317 Berlin, Germany
* Corresponding Author, juergen. dersch@dlr. de

Abstract

Greenius, a software tool for fast calculation of the technical performance and economical figures of merit for different renewable energy systems has been extended to simulate also the usage of concentrating and non-concentrating solar collectors for process heat generation. A case study for a site in southern Spain was made, varying the temperature level of the generated heat. The results show that parabolic trough collectors may provide process heat with similar specific annual yield like CPC collectors at sufficient direct irradiance and at temperatures above 140°C. They offer the potential of much higher annual yields if the can be equipped with vacuum tube receivers, which CPC’s are already using.

The study shows also the flexibility and the broad range of application of the new Greenius version.

Keywords: Renewable energy, Software, Parabolic trough, CPC, Flat plate collector

1. Introduction

The software tool Greenius has been developed at DLR since several years [1] and it is customized to perform fast calculation of the technical performance and economical figures of merit for different renewable energy systems. The calculation is done on an hourly basis for a full year using a typical meteorological data set with this temporal resolution for the specific site of interest.

Technologies already implemented in Greenius are: parabolic trough solar power plants with and without thermal storage, non-concentrating and concentrating PV, dish/stirling systems, wind energy and fuel cells. An additional technology was added now — process heat utilization by non­concentrating and concentrating collectors.

The current version of Greenius offers a great flexibility to define the collector type, the collector orientation, solar field size, storage size etc. Furthermore different load profiles (with hourly resolution for a whole year) may be defined by the user. Heat losses of the field piping are considered as well as cooling down of the whole plant during non-sunshine hours.

Many industries have a large demand for process heat in the range from 60°C to 200°C. At sites with high solar irradiation this demand could be often met by the usage of solar collectors. Due to the high oil and gas prices the usage of solar energy becomes more and more economic and at the same time it reduces the emission of green house gases.

Precondition for an economical usage of solar energy is the knowledge of expected system output and system costs in an early stage of the project. The development of a numerical tool for fast assessment of design and technology options was carried out in the context of the IEA Task 33/IV.

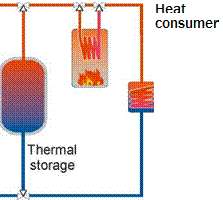
Fig. 1. Sketch of a process heat generating system with parabolic trough collectors

2. Mathematical models

The macro-spatial management is constituted of 5 distinct blocks:

Installed photovoltaic systems and types of application;

Description of type, operacional situation, fault and model of all the components of the installed photovoltaic systems;

Maintanance and training centers;

Phase of installation according to PRODEEM and Infrastructure of transmission lines, roads and airports.

Fig. 3 shows the photovoltaic pumping systems installed in the states of Paraiba (a) and Pernambuco (c). It also shows for each type of application the possibility of a more detailed filtering through a menu where the benefits and some specific aspects can be chosen: in (b), for example, the water pumping systems with higher discharge rate than 6 m3/h installed in Paraiba and in (d), the photovoltaic pumping systems in Pernambuco with manometric heights greater than 30 m.

Fig. 4 shows the batteries (a) and inversors (b) installed in Pernambuco. Additionally it shows the possibility of a more detailed filtering by a menu where specific model can be chosen: in (a) make PVX 12105 batteries and in (b) the Starpower inversors.

Fig. 5 discriminates the photovoltaic systems installed in Alagoas and Pernambuco showing the installation phase according to PRODEEM, in (a) the phase V in Paraiba and in (b) illimination in Pernambuco.

The geometry of polymeric collectors differs from standard flat plate collectors due to material properties, the mentioned production methods and the resulting degrees of freedom in design. Various approaches to design a polymeric collector are under discussion. Mechanical stresses

occur during operation and stagnation due to thermal expansion and external loads on the collectors. These stresses have to be determined for investigating the durability of the product.

The efficiency calculations mentioned above lead to operating conditions of the collector which the chosen materials have to resist. Stress distribution and deformation show potential risks for the stability and durability of the collectors. They are analyzed for various material combinations and geometries with the models used in FEM-Simulations.

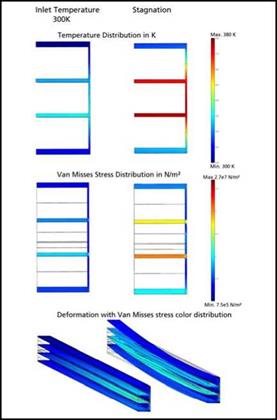
The temperature distribution depends on the position of the absorber layer whereas the temperature level is mainly influenced by the amount of irradiance, inlet temperature and the thermal losses of the collector. These parameters are varied to simulate different operating conditions. The temperature distributions during normal operation and stagnation are calculated using COMSOL Multiphysics. They are compared and validated with the results from the above mentioned simulations and common flat plate collector performances. They are used as input parameters for the numerical simulation of mechanical stresses due to thermal expansion.

Half a fluid channel of two meter length with glazing and thermal insulation was modelled 3- dimensionally including the possibilities to vary certain geometry properties and materials. The mesh and the model geometry used to calculate the mechanical stresses for an extrudable geometry are shown in Fig. 6. Due to symmetry only half of the channel had to be modelled. At both sides of the model the boundary conditions were set to be symmetrical. The calculation of the temperature distribution was done with the general

heat transfer module in COMSOL. The convective top and bottom losses were described with constant heat transfer coefficients. The ambience does not have to be modelled because of these boundary conditions. The convection in the air gaps was neither calculated instead a heat transfer coefficient was applied, too. These parameters were validated with Fluent calculations and literature references. A 2D model of half a collector crosswise to the channels was used for the simulation of an extrudable geometry. Its temperature distribution was transferred from the 3D model.

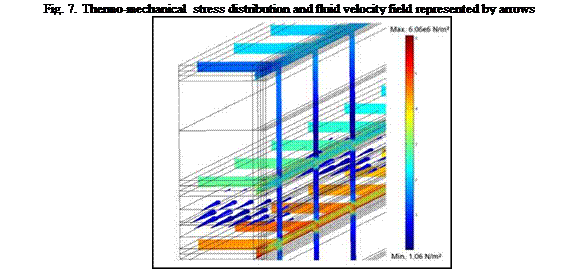The distribution of thermo-mechanical stresses shows high gradients in certain areas of the collector. Therefore the mesh was improved by choosing small finite elements in regions with big stress gradients. Due to higher temperatures of its material, the expansion of the absorber is higher than the expansion of the glazing and back frame area. Since the glazing and the back frame are connected to the absorber, the highest stresses appear at the connection between the absorber plates and the channel dividing bars. Fig. 7 shows a close view on the connecting bars. In this example the whole collector is made of the same polymer e. g. PMMA and therefore the deformation is negligible.

A co-extruded collector of two polymers with different thermal expansion coefficients shows an increasing deformation for increased inlet/fluid temperatures. The variation of the inlet temperature and resulting stress distribution are shown in Fig. 8. The images show the distributions at the outlet of the two meter long fluid channel, where the highest temperature gradients appear. In general, the mechanical stresses due to thermal expansion are acceptable for the considered geometries.

The steady state simulations show the maximum stresses and deformations which occur in the simulated operating conditions at one certain point of time and not the deterioration of the material caused by fatigue stresses. Fig. 8. Examples of simulated mechanical stress

distributions during operation and stagnation for an External loads such as snow load were examined co-extrudable collector geometry of polymers with

with a 2D model, as well. Fig. 9 shows the Van — different thermal expansion coefficients

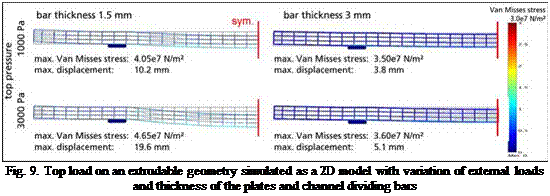Misses-Stress distributions and deformations. The variation of the bar thickness indicates that the deformations due to top pressures increase strongly for thin bars. In EN 12975 the maximum permitted deformation at 1000 Pa top load is given as 0.5 %. This threshold can be realised by increasing the thickness of the bars to about 2.7 mm for this particular design. For a load of up to 3000 Pa, the maximum stress is in acceptable range regarding PMMA with a bar thickness of 3 mm. It becomes obvious that external operational demands have to be taken into account when designing polymer collector with maximized efficiency.

4. Conclusion

Computational fluid dynamics (CFD) and FEM-Simulations are a useful tool for the identification of characteristic problems of polymer collectors. The analysis of different collector and absorber layer geometries by simulation can be used for optimisation of the parameters regarding efficiency interrelationships as well as for the discussion of durability aspects in terms of mechanical loads. It shows that the heat transfer into the fluid can possibly be improved at higher fluid velocity and further variations of the absorber geometry. The effect of the collector design on thermo­mechanical stresses could be investigated by FEM-Simulations. Main aspects of a polymer collector are now better understood and the outcomes of this work show that both the efficiency and mechanical stability can be further optimised.

5. Outlook

We want to continue with the evaluation of candidate materials and start accelerated and real time tests on selected materials to identify the most promising polymers. Further, the aim is to build demonstration collectors and to perform further tests on durability and efficiency. We would appreciate to do this research in collaboration with industrial partners.

Using numerical simulations we want to calculate and compare the energy output of different designs and material combinations and optimize these designs to develop price efficient collectors of a good quality. Additionally, we want to identify the load levels at various service conditions and investigate different absorber coatings and their application ranges.

The daily temperature cycles and the stagnation situations in the summer, which the collector materials have to resist, cause material aging. Therefore time stepwise simulations using weather data and system operating parameters can lead to information on material aging, and to an estimate of the energy gain by taking into account the changes in the material parameters due to the thermal-mechanical stresses and other degradation appearing at operating conditions in future simulations.

Acknowledgements

The work was funded by the German Federal Ministry of Education and Research (BMBF FKz:

01RI05201).The authors also want to thank all the partners of IEA SHC Task 39 for their input,

especially the French colleagues from INES and CEA.

References

[1] Clough, Roger; Billingham, Norman; Gillen, Kenneth (editor): Polymer Durability: Degradation, Stabilization, and Lifetime Prediction. American Chemical Society, Washington 1996

[2] Duffie, John; Beckman, William: Solar Engineering of Thermal Processes. 3rd edition, Hoboken, New Jersey : John Wiley & Sons, 2006

[3] Kohl, Michael; Franke, Hannes; Stricker, Eva; Weifi, Karl-Anders: Polymeric materials for solar thermal collectors — a feasibility study. In: ESTIF: ESTEC 2007, 3rd European Thermal Energy Conference (proceedings). Freiburg : ESTIF, 2007, S. 223-229

[4] Jack, Steffen: Simulationsgestutzte Qualifizierung neuer Konzepte zur Gestaltung von thermischen Solarkollektoren auf Polymerbasis. Freiburg : Fraunhofer ISE; FHTW Berlin, 2008

The vacuum tube collector implemented and simulated in OptiCAD was also investigated experimentally at the outdoor test facility of the “Test Centre for Solar Thermal Systems (PZTS)” at the Fraunhofer ISE according to the guidelines of EN 12975-2. The tests include the measurement of the optical efficiency p0 and the IAM-values in the longitudinal and transversal plane.

The following problem has to be considered: The measured optical efficiencies are evaluated with respect to the measured global radiation. However, the simulations in OptiCAD are conducted by applying direct radiation. In order to compare simulated IAM-values with measured ones the specific fraction of diffuse radiation recorded during the measurement has to be taken into account. Moreover, during the IAM measurements — which are outdoor measurements — different levels of diffuse radiation may have occurred. This is considered in the comparison to the simulated IAM- values. In the measurements, also the diffuse radiation is not isotropic but may vary over the hemisphere and the surroundings within the viewing angle of the collector. However, in order to simplify the process the adjustment of the measured values is carried out by assuming a constant isotropic distribution. The tilt angle of the collector is also not taken into account.

Figure 6 shows the simulated transversal IAM of the vacuum tube collector over the incidence angle in transversal direction. Furthermore, the measured transversal IAM-values at their corresponding incidence angle of 20°, 40° and 60° are charted. Those values were adjusted as described above.

It can be seen that the measured values and the adjusted ones are almost exactly the same. It should be mentioned that in the measurements the fraction of diffuse irradiation is rather constant which contributes to the fact that the adjustments are small. Furthermore, the figure shows that the simulation result fits very well the measured data whereby the simulation output can be regarded as validated.

2. Conclusion

Ray-tracing simulations can be used as a powerful tool for the development of collectors [5]. Furthermore, the acceptance of diffuse radiation of a collector expressed as the diffuse IAM can be determined by utilisation of simulated IAM-values for direct radiation.

Once a certain collector type (single glazed flat-plate collector, vacuum tube collector with a given distance of vacuum tubes, with or without reflector, etc.) is modelled in OptiCAD, it is rather quick to carry out parameter variations and investigate different development possibilities. This may concern geometrical and material options. However, the result shown in Figure 6 requires detailed information about the collector parameters. The quality and exactness of the input data directly influence the quality of the results of ray-tracing simulations. With respect to the comparison of simulated against measured IAM-values, the model for the distribution of the diffuse radiation on the hemisphere has to be taken into consideration.

References

[1] Hefi, Stefan: Raytracing-Untersuchungen fur die Entwicklung von Prozesswarme-Kollektoren. In: 18. OTTI Symposium Thermische Solarenergie. Proceedings. Bad Staffelstein, 23.-25. april 2008, p. 416 — 421.

[2] Rommel, Matthias (Fraunhofer ISE); Weiss, Werner (AEE INTEC): Process Heat Collectors. State of the Art within Task 33/IV. Gleisdorf, Austria: AEE INTEC 2008.

Available: http://www. iea-shc. org/publications/downloads/task33-Process Heat Collectors. pdf

[3] Welford, W. T., Winston, R.: The Optics of Nonimaging Concentrators: Light and Solar Energy. San Diego, California; London: Academic Press, Inc. 1978

[4] TRNSYS 16: a TRaNsient SYstem Simulation program. Volume 5 — mathematical reference. Type 71, p. 5-343

[5] Geisshusler, Simon: IAM (Winkelfaktoren) Raytracing Simulationen von Solarthermischen Kollektoren. In: 17. OTTI Symposium Thermische Solarenergie. Proceedings. Bad Staffelstein, 09.-11. may 2007, p. 248 — 250.

Modelling complex systems within TRNSYS SIMULATION STUDIO

S. Kuethe*, C. Wilhelms, K. Zass, R. Heinzen, K. Vajen and U. Jordan

Kassel University, Institute for Thermal Energy Technology, 34125 Kassel, Germany
* Corresponding Author, solar@uni-kassel. de

Abstract

Solar thermal systems progress in complexity as the technology advances. Development and optimization of these systems is often carried out with the help of flexible numerical simulation tools like TRNSYS. With increasing complexity, maintaining flexibility and structure of the simulation model is an important issue. Therefore, Version 16 of TRNSYS comes along with the graphical user interface SIMULATION STUDIO. It assists the user in setting up the model. Furthermore, a graphical system representation is available automatically. However, for complex systems containing a lot of components and interconnections the system understanding and usability of the model gets difficult. Due to this fact this paper describes a new structure level introduced to SIMULATION STUDIO. Like TRNSYS itself, it also pursues a modular approach by organizing a model in several subsystems, where a subsystem is a collection of components. These subsystems are connected to each other with uniform interfaces only. This results in modularity on the component as well as on the subsystem level and allows the replacement of subsystems in SIMULATION STUDIO in a simple way. The solar thermal system developed within Task 32 of the Solar Heating and Cooling Programme of the International Energy Agency (IEA-SHC Task 32) has been implemented using the new approach.

Keywords: solar thermal, simulations, modelling complex systems, TRNSYS

1. Introduction

TRNSYS [1] is the most commonly used numerical simulation tool for development and investigation of solar thermal systems. Since Version 16, it comes along with the graphical user interface SIMULATION STUDIO. Besides the assistance of generating the TRNSYS ASCII input file, the graphical representation of the model is supposed to improve the maintenance of it. In addition, it should help to decrease the time for third party users to get familiar with new models. However, with increasing complexity of a model the graphical representation gets confusing due to the crossing of many interconnections between the several components (see Fig. 1). This fact leads to difficulties of the system understanding regarding the interaction between the components.

Portugal /

No_Parsons (Type9а) Internal Bams (Type 9a)

Fig. 1: Graphical representation of a complex model with a lot of overlapping interconnections between the

components in SIMULATION STUDIO.

Furthermore, the replacement of system parts like a collector loop of a solar thermal system is not possible in a simple way. SIMULATION STUDIO already has got two options in terms of structuring components. On the one hand components can be arranged on several layers, which can be hidden and unhidden by demand, and on the other hand components can be collected in macros, where the input and output dialog of a macro contains all inputs and outputs of the components within the macro. In the graphical representation the collected components of the macro are replaced by one symbol only. Unfortunately, both features only help to improve the design quality but do not provide simple to handle removals or transfers of complete system parts to other models. Therefore, a new structure level is introduced to SIMULATION STUDIO. It follows the modular concept of TRNSYS by defining subsystems, in which components are grouped. The subsystems are connected via uniform implemented interfaces containing all required inputs and outputs of the subsystems. As interfaces simple EQUATION blocks are used in SIMULATION STUDIO and connections of subsystems are realized via the defined interfaces only. The interfaces are implemented in a way that a replacement of subsystems is possible without deleting or reconfiguring graphical links between the subsystems.

Influences of climate, load profile and energy storage on the optimum inclination and orientation for thermal and photovoltaic solar energy

collectors

Brian Norton

Dublin Energy Lab Dublin Institute of Technology Dublin, Ireland president@dit. ie Abstract

Climatic and operational factors influencing the optimal orientation of solar energy, primarily photovoltaic, collectors are discussed in the context of relevant previous research. An example is provided of how being in a climate with diffuse components of insolation and winter loads that are generally high gives rise to an optimal inclination with a far greater slope angle than the latitude.

Keywords: Photovoltaics, system design, climate, inclination, orientation.

1. Introduction

When building integrated photovoltaics (BIPV) walls, roofs, and awnings provide fully — integrated electricity generation while also serving as part of the weather protective building envelope [1 — 4]. BIPV can also serve as window shading devices, semi-transparent glass facades, exterior cladding panels, skylights, parapets or roofing systems [5 — 19]. BIPV system output depends on [20 — 22] (i) the availability of and access to solar radiation as determined by climate, inclination and orientation of available building surfaces [23, 24], (ii) PV efficiency and its degradation with time [25], (iii) efficiency of balance of system components. [26], coupling to the electrical network, electrical wiring resistance and voltage drop in diodes [27,28] and (iv) shading, over-shading [29] and accumulation of dirt, dust or snow.

2. Design Issues

Grid-connected PV system economic viability depends on electrical loads and utility prices [30, 31]. PV output varies according to their specific spectral selectivity as direct and diffuse insolation spectra alter with air mass and relative humidity [32; 33, 34], so better spectral matching raises PV efficiency [35]. Larger air mass at low sun angles (the incident spectrum being towards red) decreases PV efficiency. [36]. PV surface reflection loss depends orientation, inclination and location [34, 37, 38]. Measured yearly reflection losses have ranged 6.7% to 10. 8% [39, 40]. Reflection losses are lessened by the inclusion of anti­reflection coatings. Accrual of dirt on a PV surface reduces insolation transmission annually by 2% to 8% [37, 41, 42] but in dry summers could be over 20% [43; 44] depending on the PV surface, local dust sources, cleaning frequency (by rain or manually) [45] and PV surface

inclination [46]. The annual system performance ratio [1] of a roof-mounted BIPV at latitude of 54°N was 18.1% lower than the maximum [47]. At 35.7°N latitude maximum annual energy was obtained for the surface with tilt angle 29°. [48]. For both these locations, these more-inclined optimal inclinations show the contribution diffuse insolation can make to the total solar energy incident annually on a BIPV array. As illustrated in figure 1, there is a broad trend in Europe for diffuse components to be larger (i. e., the clearness index is lower) at higher latitudes [24].

For seasonally-tracking arrays, annual PV output can be 94% to 96% of the maximum annual PV output when optimum tilt angle is selected only once a year and 99% of the maximum annual PV output if the optimum angle is adjusted twice a year [49]. Different methods are available to obtain optimum tilt of a PV system based on the latitude, local climates, insolation conditions and energy demand [47, 50 — 56] and location-pecific measurements have been reported of the seasonal dependence of PV system performance [57 — 64]. An autonomous solar energy system is defined as not being grid-connected: such are common from free-standing urban street furniture such as solar powered parking charge maters and solar lit and powered ticketing in bus shelters to remote systems ranging from buildings in isolated locations to solar water pumps in deserts [65 — 66]. Such systems satisfy a particular temporal load pattern in the specific weather variations associated with the prevailing climate. From a solar energy system design perspective, climate and load primarily determine the optimal inclination of collection. This interaction is, however complex as the load a function of the climate either directly or indirectly, in time or magnitude. Using a validated simulation model, the maximum annual system performance ratio of a roof mounted BIPV system at a latitude of 54°N in the UK was found to be for a south-facing surface inclined at 20°.[47]. Figure 2 shows the breakdown of influences that cause the optimal inclination in this particular example to 30° different from the latitude

Direct

The example in figure 3 does not have energy storage. The function of energy storage is to enable loads to be met by solar energy systems nocturnally and, more generally, when insolation would be insufficient. The optimal inclination with appropriately sized storage would be the optimal plane position for the collection of both the prevailing direct and diffuse insolation components. Similarly, with storage, there is seldom benefit from non-equatorial — facing (i. e., south-facing and north-facing in the northern and southern hemispheres respectively) orientations. However in applications that make transient use of solar energy such as cooking, incorrect inclination and orientation can lead to poor performance.

References

1. Sick F. & Erge T., (1996), Photovoltaics in Buildings: A Design Handbook for Architects and Engineers, James & James Limited, London UK,

2. Bendel, C., Gummich, D., & Rudolf, U. (1995) Development of photovoltaic facade elements: technical aspects of multifunctional PV-facades, 13th European Photovoltaic Solar Energy Conf, Nice, October, 2168-2170.

3. Bahaj, A. S. & Foote, J. S. (1994) Photovoltaic cladding, a design approach for panels and curtain walling for new and existing buildings, 12th European Photovoltaic Solar Energy Conference, Amsterdam, April, 1097-1099.

4. Brogren M., Wennerberg J., Kapper R., & Karlsson B., (2003), Design of Concentrating Elements with CIS Thin-Film Solar Cells for Facade Integration, Solar Energy Materials & Solar Cells, 75,. 567-575.

5. Bowden, S., Wenham, S. R., Coffey, P., Dickinson, M. R. & Green, M. A. (1993) High efficiency photovoltaic roof tile with static concentrator, IEEE Photovoltaic Specialists Conference, Louisville, May, 1068-1072.

6. Izu, M., Ovshinsky, H., Whelnan, K., Fatalski, L., Ovshinsky, S., Glatefelter, T., Younman, K., Hoffman, K., Banerjee, K., Yang, J. & Guha, S. (1994) Lightweight flexible rooftop PV module, IEEE PV Specialists Conf, Waikoloa,, Dec, 990-993.

7. Hagemann, I. (1996), PV in buildings-the influence of PV on the design and planning process of a building, Renewable Energy, 8, 1-4, 467-470.

8. Bonvin, J., Roecker, C., Affolter, P. & Muller, A. (1997) SOLBAC flat roof system and first installations, 14th European Photovoltaic Solar Energy Conference, Barcelona, Spain, July, 1849­1850.

9. Bahaj, A. S., Ballard, J. R., James, P. A.B & Mucci, P. E.R (1998) A new approach to photovoltaic roof tiles, 2nd World Conference and Exhibition on Photovoltaic Solar Energy Conversion, Vienna, Austria, July, 2690-2693.

10. Zacharopoulos A., Eames P. C., McLarnon D., & Norton B., (2000), Linear Dielectric Non­Imaging Concentrating Covers For PV Integrated Building Facades, Solar Energy, 68, 5, 439-452.

11. Benemann, J. (1994) Multifunctional solar facades — a new challenge for photovoltaic, Conference Record of the IEEE Photovoltaic Specialists Conference, 1, Waikoloa, HI, USA, December, 784­787.

12. Maurus H., Schmid M., Blersch B., Lechner P. & Schade H. (2004) PV for Buildings, ReFocus, December, 22-27.

13. Mallick, T. K., Eames, P. C., & Norton, B, (2002), Asymmetric Compound Parabolic Photovoltaic Concentrators for Building Integration in the UK: An Optical Analysis, World Renewable Energy Cong July 2002, Koln,

14. Mallick, T. K., Eames, P. C., & Norton, B, (2002) App of Comp Fluid Dynamics to Predict the Thermo-Fluid Behaviour of a Parabolic Asymmetric pv Concentrator, World Renewable Energy Cong, July 2002, Koln,.

15. Mallick, T. K., Eames P. C., Hyde T. J., & Norton B., (2004), The design and exp characterisation of an asymmetric compound parabolic pv concentrator for building facade integ in the UK, Sol Energy, 77, 3, 319-327.

16. Mallick T. K., Eames P. C., Hyde T. J., & Norton B., (2004), Exp characterisation of an asymmetric compound parabolic pv concentrator designed for building integration in the UK, Int J of Ambient Energy, 25, 2,85-96.

17. Mallick, T. K., Eames P. C., & Norton B., (2006), Non-Concentrating and Asymmetric Compound Parabolic Concentrating Building Facade Integrated Photovoltaics: An Exp Comparison, Sol Energy, 80, 7, 834-849.

18. Mallick, T. K., Eames P. C., & Norton B., (2007), Using Air Flow to Alleviate Temperature Elevations in Solar Cells within Asymmetric Compound Parabolic Concentrators, Solar Energy, 81, 173-184.

19. Miller W., Brown E. & Livezey R. J. (2005) Building-Integrated Photovoltaics for Low-slope Commercial Roofs, ASME Journal of Solar Energy Engineering, 127, 307-313

20. Kaye, R. J. (1994) A new approach to optimal sizing of components in stand-alone photovoltaic power systems, 24th IEEE Photovoltaic Specialists Conference, Hawaii, USA, December, 1192­1195.

21. Sidrach-de-Cardona, M & Lopez L. M. (1999) Performance analysis of a grid-connected photovoltaic system, Energy, 24, 93-102.

22. Imamura, M. S., Helm, P. & Palz, W. (1992) Photovoltaic system technology a European Handbook, H S Stephens and Associates, Bedford, England.

23 Norton, B., (1992) Solar energy thermal technology, Springer, Heidelberg, Germany

24. Waide, P. A. & Norton B. (2003) Variation of insolation transmission with glazing plane position and shy conditions, ASME Journal of Solar Energy Engineering, 125, 182-9

25. Simmons, A. D. & Infield, D. G. (1996) Grid-connected amorphous silicon photovoltaic array, Progress in Photovoltaics: Research and Applications, 4, 381-388.

26. Miguel, A. D., Bilbao, J., Cazorro, J. R.S. & Martin, C. (2002) Performance analysis of a grid — connected PV system in a rural site in the Northwest of Spain, World Renewable Energy Congress VII, Cologne, July.

27. Baltus, C. W.A, Eikelboom, J. A. & van Zolingen, R. J.C. (1997) Analytical monitoring of losses in PV systems, 14th European Photovoltaic Solar Energy Conference, Barcelona, Spain, July, 1547­1550.

28. Bahaj, A. S., Braid, R. M. & James, P. A.B. (2001) An assessment of the building integrated pv facade and it’s operational mismatch losses at Southampton Univ, Renew En in Maritime Island Clim, Belfast, Sept, 111-118.

29. Alonso, M. C., Arribas, L. M., Chenlo, F. & Cruz, I. (1997) Shading effect on a roof integrated grid — connected PV plant, 14th European Photovoltaic Solar Energy Conference, Barcelona, Spain, July, 1891-1893.

30. Watt M., Kaye R. J., Travers D., & MacGill I., (1998a), “Assessing the Potential for PV in Buildings”, 14th European Photovoltaic Solar Energy Conference and Exhibition, Barcelona, Spain, 1879-1882.

31. Mondol J D, Yohanis Y G. & Norton B (2008), Solar radiation modelling for the simulation of photovoltaic systems, Renewable Energy, 33, 1109-1120

32. Hirata, Y. & Tani, T. (1994) Evaluation of photovoltaic modules considering spectral solar radiation, Electrical engineering in Japan, 114, 8, 93-105.

33. Nann S. & Emery, K. (1992) Spectral effects on PV-device rating, Solar Energy Materials and Solar Cells, 27, 189-216.

34. Bucher, K. (1997) Site dependence of the energy collection of PV modules, Solar Energy Materials and Solar Cells, 47, 85-94.

35. Ruther, R. & Dacoregio, M. M. (2000) Performance assessment of a 2 kWp grid-connected, building integrated, amorphous silicon photovoltaic installation in Brazil, Prog. in Photovoltaics: Research & App, 8, 257-266.

36. Pratt, R, G. & Burdik, J. (1988) Performance of a 4 kW amorphous-silicon alloy photovoltaic array at Okland Community College, Aurban Hills, Michigan, IEEE Photovoltaic Specialists Conf, Las Vegas,, Sept, 1272-1277.

37. Reinders, A. H.M. E, Dijk, V. A.P., Wiemken, E. & Turkenburg, E. (1999) Technical and economic analysis of grid-connected PV system by means of simulation, Prog in Photovoltaics: Research & Appl, 7, 71-82.

38. Martin, N. & Ruiz, J. M. (2001) Calculation of the PV modules angular losses under field conditions by means of an analytical model, Solar Energy Materials and Solar Cells, 70, 25-38.

39. Lanzerstorfer, S., Bauer, G. & Wilk, H. (1995) Losses by reflection of crystalline PV modules, 13th European Photovoltaic Solar Energy Conference, Nice, France, October, 2294-2297.

40. Preu, R., Kleiss, G., Reiche, K. & Bucher, K. (1995) PV-module reflection losses: measurement, simulation and influence on energy yield and performance ratio, 13th Euro Photovoltaic Sol Energy Conf, Nice, Oct, 1465-68.

41. Goossens D. & Kerschaever E. V., (1999), Aeolian Dust Deposition on Photovoltaic solar cells:

The Effects of Wind Velocity and Airborne Dust Concentration on Cell Performance, Solar Energy, 66, 277-289.

42. Gonzalez, C. (1986) Photovoltaic array loss mechanisms, Solar Cell, 18, 373-382.

43. Maag, C. R. Jr. (1977) Outdoor weathering performance of solar electric generators, Journal of Energy, 1, 6, 376-381.

44. Townsend, T. U. & Whitaker, C. M. (1997) Measured vs. ideal insolation on PV structures, 26th IEEE Photovoltaic Specialists Conference, Anaheim, CA, October, 1201-1204.

45. Hoffman, A. R. & Maag, C. R. (1980) Airborne particulate soiling of terrestrial photovoltaic modules and cover materials, Proc, Ann Tech Meeting-Institute of Environmental Sci, Philadelphia, PA, USA, May, 229-236.

46. Nakamura, H., Yamada, T, Sugiura, T., Sakuta, K. & Kurokawa, K. (2001) Data analysis on solar irradiance and performance characteristics of solar modules with a test facility of various tilted angles and directions, Sol En Mat and Sol Cells, 67, 591-600.

47. Mondol J D, Yohanis Y G. and Norton B (2007a), Comparison of measured and predicted long term performance of grid a connected photovoltaic system, Energy Conversion and Management, 48, 1065-1080

48. Soleimani, E. A, Farhangi, S. & Zabihi, M. S. (2001) The effect of tilt angle, air pollution on performance of photovoltaic systems in Tehran, Renewable Energy, 24, 459-468.

49. Balouktsis, A., Tsanakas, D. & Vachtsevanos, G. (1987) On the optimum tilt angle of a photovoltaic array, International Journal of Solar Energy, 5, 153-169.

50. Tsalides, P. & Thanailakis, A. (1985) Direct computation of the array optimum tilt angle in constant-tilt photovoltaic systems, Solar Cells, 14, 83-94.

51. Kern, J. & Harris, I. (1975) On the optimum tilt of a solar collector, Solar Energy, 17, 97-102.

52. Bari, S. (2000) Optimum slope angle and orientation of solar collectors for different periods of possible utilization, Energy Conversion and Management, 41, 855-860.

53. Mondol J D, Yohanis Y G. & Norton B (2007b), The impact of array inclination and orientation on the performance of a grid-connected photovoltaic system, Renewable Energy, 32, 118-140

54. Mondol J D, Yohanis Y G. & Norton B (2006a), Optimal sizing of array and inverter for grid — connected photovoltaic systems, Solar Energy, 80, 1517-1539

55. Mondol J D, Yohanis Y, Smyth M & Norton B (2006b), Long term performance analysis of a grid connected photovoltaic system in Northern Ireland, Energy Conversion and Management, 47, 2925­2947

56. Mondol J. D., Yohanis Y. G., Smyth M. & Norton B. (2005), Long-term validated simulation of a building integrated photovoltaic system, Solar Energy, 78, 163-176

57. Ruther, R. (1998) Experiences and operational results of the first grid-connected, building integrated, thin film photovoltaic installation in Brazil, 2nd World Conf on Photovoltaic Sol Energy Conv, Vienna, July, 2655-2658.

58. Marion, B. & Atmaram, G. (1990) Seasonal performance of three grid-connected PV systems, Conference Record of the IEEE Photovoltaic Specialists Conference, 2, Kissimimee, FL, USA, May, 1030-1037.

59. Oladiran, M. T. (1995) Mean global radiation captured by inclined collectors at various surface azimuth angles in Nigeria, Applied Energy, 52, 317-330.

60. Akhmad, K., Belley, F., Kitamura, A., Yamamoto, F. & Akita, S. (1994) Effect of installation conditions on the output characteristics of photovoltaic modules, IEEE Photovoltaic Specialists Conf, Hawaii, Dec. 730-733.

61. Sopitpan, S., Changmuang, P. & Panyakeow, S. (2001) Monitoring and data analysis of a PV system connected to a grid for home applications, Solar Energy Materials and Solar Cells, 67, 481­490.

62. Pearsall, N. M., Hynes, K. M. & Hill, R. (1997) Analysis of operation of the Northumberland building photovoltaic facade, 14th European Photovoltaic Solar Energy Conference, Barcelona, Spain, July, 1968-1971.

63. Molenbroek, E. C., Leenders, F., Kil, A. J., Hoekstra, K. J., Deege, P. & Schoen, A. J.N. (1998) Field experience with grid connected, roof integrated amorphous silicon PV systems in the Netherlands, 2nd World Conference on Photovoltaic Solar Energy Conversion, Vienna, July, 2583-2586.

64. Itoh, M., Takahashi, H., Fujii, T., Takakura, H., Hamakawa, Y. & Matsumoto, Y. (2001) Evaluation of electric energy performance by democratic module PV system field test, Sol Energy Mat & Sol Cells, 67, 435-440.

65. Odeh, I., Y. Yohanis and B. Norton, Influence of pumping head, insolation & PV array size on PV water pumping system performance, Solar Energy. 80, 51-64, 2006

66. Odeh I., Y. G. Yohanis and B. Norton., Economic viability of PV water pumping systems, Solar Energy. 80, 850-860, 2006

S. Thomas* and P. Andre

Department of sciences and environmental management, University of Liege 185 Avenue de Longwy, 6700 ARLON, Belgium Corresponding Author, sebastien. thomas@ulg. ac. be

Abstract

To minimize environmental impact and CO2 production associated with air-conditioning system operation, it is reasonable to evaluate the prospects of a clean energy source. The targets of the study are to evaluate cooling energy consumption to maintain thermal comfort in an office building and to point out solar energy to satisfy these cooling needs. Simulations were carried out with three different cooling systems in the same operating conditions to determine as accurately as possible the potential use of solar energy. For comparison purpose, the base case is a classical air-conditioning system (heat pump for cooling, gas boiler for heating). Two other configurations were simulated: a classical vapour compression system fed by photovoltaic panels and electricity grid as back-up and, absorption chiller fed by solar thermal panel field and by gas boiler. In the three chosen locations (Paris, Lisbon and Stockholm), results shown that installing photovoltaic panels on the roof is really interesting from the primary energy consumption point of view.

Keywords: Solar cooling, absorption, photovoltaic, TRNSYS

1. Introduction

The present energy context is characterized by the imminent end of the era of fossil fuels and the environmental impact of their operation. Energy demand growth, local pollution, global climate change, … are problems that must be taken into account. It seems urgent to reconsider our way of life and design equipments as to minimise their energy consumption. Most air-conditioning equipments are currently electrically driven vapour compression systems. According to the International Institute of Refrigeration (IRR) [1], 15% of the world’s electricity is used for refrigeration and cooling. Moreover, the growth of cooling needs and consequently electricity consumption for cooling is an indisputable fact.

Using renewable energy such as solar energy is really feasible for air conditioning in building. Different technologies exist and can be compared based upon different characteristics: energy consumption, cost of the whole equipment, … The study is dedicated to office buildings which require especially high comfort levels and have often high heat gains due to glazed facades and electrical equipment. Small scale (round 5-10 kW) applications became recently market available. For large scale absorption and adsorption chillers the technology is more mature because of existing system driven by waste heat (coming generally from a cogeneration unit). In this work the emphasis is put on available technologies, key equipments are market available and data is taken directly from manufacturer.

The comparison exercise is realized on a theoretical office building. To point out use of solar energy in this building, three test cases have been defined. The first one is used as reference as it is a usual system implementation in real office building. For each case, three locations have been simulated using Meteonorm data files: Paris (Montsouris station), Stockholm (Arlanda station) and Lisbon.

Especially for the last two cases, several aspects are to be addressed in order to provide a suitable solar air conditioning solution:

• Solar collectors

• Refrigeration equipment (chiller)

• Building

• Climate

Simulation of all these elements as well as links between them requires a very flexible simulation software. The dynamic simulation environment TRNSYS [2] is applied in this study. It makes possible the whole system simulation as well as the implementation of new models.

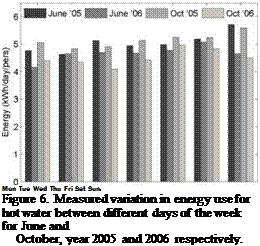The variation in measured hot water use was also investigated on a daily basis to examine a possible difference between different days of the week. The results are found in Figure 6 for two different months the two years of available data. The trend is similar for both years and the variation between different days is small. Measured data seem to follow a similar pattern for 2005 and 2006 respectively, where the daily use is lower in 2006. Data for a certain month, however, does not coincide for the two years under investigation.

4. Discussion

The measured hot water use in the 24 apartments is similar for the two years investigated so far. The minimum in load is located in July and August, although the use is generally lower during 2006. As was also concluded in the analysis in [7] this indicates the impact of individual habits on the consumption profile. Individual habits, and the energy use in the wider context of everyday activities, can be further investigated by time diaries, which constitute the foundation of the presented model.

According to the results obtained in this study, when comparing the modelled profiles with measured, the model gives a similar, but somewhat lower hot water use. The overall load profiles, on the other hand, follow more or less the same pattern. The difference between winter time and summer time may imply that the model describes winter time better. Measurements in Malmo, Sweden, however shows morning peaks at 6-8 a. m. in weekdays and 9-10 a. m. in weekend days [9], which may indicate that the difference between summer and winter months is rather due to the routines of the particular inhabitants. The number of measured households is however too low to draw any evident conclusion.

The magnitude of the hot water use can be further compared to the study performed by the Swedish Energy Agency which shows a surprisingly low DHW use of 0.9 MWh per person and year for apartments [1]. In that study only four apartments were measured. The fact that the model predicts an energy use between that measurement study and the one investigated in this paper, and closer to the more extensive one, indicates that the model assumptions are in the right range.

The modelled profiles will be used in future studies on solar heating by introducing different profiles in dynamic simulations in the simulation tool TRNSYS. The possibility to utilize solar heat will be investigated as depending on different behaviours found in the material on time-use. Furthermore, the advantages with individual as well as joint solar heating system for a residential area will be investigated to further raise the question of tap water supply systems for low-energy buildings.

The current model only generates average profiles for one weekday and one weekend day and is not taking seasonal and weekly variations in load into account. An improvement would be to introduce those variations in the model, for example by statistical means similar to those used in Jordan et al [2]. By letting the daily individual distribution be the foundation, but vary it with day of the week and time of the year, realistic yearly profiles can be generated from single days.

More extensive measurement surveys, including a statistically significant number and distribution of households, as well as measuring hot water use in the same households as where time diaries are recorded, would be desirable to enable a more thorough validation of the model. This kind of studies are however not available at present. Although there may be deviations between the model and measurements the modelled profiles constitute an improved description of hot water use in households compared to the very simplified load profiles that are normally used.

5. Conclusion

Comparisons between modelled profiles and measurements in 24 apartments show good agreement both in magnitude and the typical distribution in time. This indicates that the model describes Swedish domestic hot water use rather well and that time-use data can be utilized for cheap and straightforward

energy estimations in households, either as an alternative, or as a complement, to detailed hot water measurements.

Detailed investigations of variations in hot water demand over the year show a clear minimum in demand during summer due to vacation periods. The average hourly distribution over the day more or less coincide between different months, and there is only a small difference in load between the days of the week, although absence and different habits seem to influence the weekly distribution between summer and autumn.

7. Acknowledgement

The work has been carried out under the auspices of The Energy Systems Programme, which is primarily financed by the Swedish Energy Agency. We also want to thank Mimer, Malarenergy, Eskilstuna Kommunfastigheter and Eskilstuna Energi och Miljo for support. Thanks to Joakim Widen, Uppsala University, for converting the original time-use data to matrixes to be used in this paper.

References

[1] Wahlstrom A, R. Nordman and U. Pettersson (2008) Matning av kall- och varmvatten i tio hushall, SP Technical Research Institute of Sweden and the Swedish Energy Agency, ER 2008:14, ISSN 1403-1892. In Swedish.

[2] Jordan U. and K. Vajen, Influence of the DHW load profile on the fractional energy savings: A case study of a solar combi-system with TRNSYS simulations, Solar Energy 69 (2000) 197-208.

[3] Wollerstrand J. (1997). District heating substations: performance, operation and design. Doctoral thesis from Department of Heat and Power Engineering, Lund Institute of Technology, Sweden.

[4] Holmberg S (1987). Flow rates and power requirements in the design of water services. Doctoral thesis from Department of Heating and Ventilation Technology, Royal Institute of Technology, Sweden.

[5] Lundh M., Wackelgard E. and K. Ellegard (2008) Design of hot water user profiles for Swedish households based on time diaries, International Conference on Green Energy with energy management and IT,

Stockholm, Sweden, March 12-13 2008.

[6] Widen J, M. Lundh, I. Vassileva, E. Dahlquist, K. Ellegard and E. Wackelgard (2008) Constructing load profiles for household electricity and hot water from time-use data — modelling approach and validation. Submitted to Energy and Buildings.

[7] Vassileva I., C. Bartusch, E. Dahlquist (2008) Differences in electricity and hot water consumption in apartments of different sizes, International Conference on Green Energy with energy management and IT, Stockholm, Sweden, March 12-13 2008.

[8] Ellegard K. and M. Cooper (2004) Complexity in daily life — a 3D visualisation showing activity patterns in their contexts. eIJTOUR (Electronic International Journal of Time Use Research), Vol 1.

[9] Bagge H. (2007) Energy Use in Multi-family Dwellings — Measurements and Methods of Analysis, Licentiate Thesis, Department of Building Physics, Lund University, Sweden.

The tested aluminium ICS-SWH was designed and manufactured with 3mm thick aluminium sheets incorporating fins to improve the thermal efficiency and structural stability of the heater.

The water tank was placed in a hard wooden box insulated with layer of fibre glass wool on all sides and bottom as shown in Figure 1. A gap of 35mm between the absorber plate and glazing was used to reduce heat losses by restricting air movement.

1.1. Concentrating and tracking system

With the intention of creating a practical and economical solar concentrator that can provide high- concentration sunlight, a parabolic dish that was developed to collect radio transmissions from cable television satellites in past has been converted into a highly reflective concentrator. The diameter of the parabolic dish is 1.2 meter and its focal length is 0.456 meter and the projected aperture area is about 1.1 square meters. As a reflecting surface we used reflecting film which is cheap and easy to buy locally.

It is well known that concentration necessarily leads to an unavoidable reduction of the angular aperture (acceptance angle) [6,7] of any collector system. Concentrators are thus limited to collecting only those rays coming from a narrow solid angle cone centre on the solar disc, i. e. mainly beam radiation. Therefore, whenever a system is intended to operate with an effective concentration ratio larger than 6 X [7], it must be provided with sun tracking to collect a reasonable fraction of this available beam radiation. Point-focus optics generally require that the concentrator track about two axes so that it is always pointed at the sun, and the focused light falls on the cell. From a mechanical standpoint, two-axis tracking is more complex than one-axis tracking; however, point focus systems are also capable of higher concentration ratio and hence lower cell cost.

A two axes sun tracking system will be applied to increase the solar system efficiency. As we know, the greater the accuracy in computing the sun position, the greater the margin of tolerance will be for other sources of error, such as optical and mechanical, that may arise within the concentrating system. Blanco et al. [8] reviewed the solar literature concerning determination of the sun position published in the last decades. In their paper, they introduced the new, more accurate and simpler algorithm that will be used here. Moreover, a programmable logic controller system will be designed and constructed.

The CPV receiver is composed of solar cells, electrical connections and vessel to provide liquid to cool the cells. The design concepts of the CPV receiver are given in Fig. 1. High performance photovoltaic cells will be used to make the system efficiency higher. Moreover, solar cells will be immersed in a dielectric liquid that will provide an effective cooling to the solar cells. The liquid enters the vessel with the temperature Tfi and leaves at the temperature Tfo. Heat from solar cells is

transferred to the liquid through convection and conduction. The size of the vessel will be changed with the solar modules to provide effective cooling.

Northeast Of Brazil

Part I — General Description And Methodology

C. Tfba1*, A. L. B. Candeias2, N. Fraidenraich1, E. M. de S. Barbosa1, P. B. de Carvalho Neto3

and J. B. de Melo Filho3

1Departamento de Energia Nuclear da Universidade Federal de Pernambuco
Av. Prof. Luiz Freire, 1000 — CDU, CEP 50.740-540, Recife, Pernambuco, Brazil

2

Departamento de Engenharia Cartografica da Universidade Federal de Pernambuco
Av. Academico Helio Ramos, s/n — CDU, Recife, Pernambuco, Brazil
3Companhia Hidro Eletrica do Sao Francisco — DTG — CHESF
Rua Delmiro Gouveia, 333 — Bongi, CEP 50761-901, Recife, Pernambuco, Brazil
Corresponding Author.tiba@ufpe. br or chigueru. tiba@pa. cnpq. br

Abstract

This work describes the development of a management and planning system on a GIS (Geographic Information System) platform destined to decision makers that is, administrators, planners or consultants in renewable energies. It was conceived to deal with the management and planning of solar photovoltaic systems, biomass and aeolics in rural regions of the Northeast of Brazil. The prototype of the GIS tool covers an area of 183, 500 km2 and is made up of three principal blocks: management of installed renewable systems, inclusion (planning) of new renewable systems and updating of the data banks. The system was developed mainly for PV systems as a support tool for management and planning of the Energy Development Program for States and Municipalities (PRODEEM), a program for inclusion of large scale solar photovoltaic energy, in the rural environment, conducted by the Ministry of Mines and Energy of Brazil. Due to the limitation of space, only a general description and the methodology used for its development will be described here. A detailed description of the functionalities of the SIGA SOL 1.0 (Geographic Information System Applied to Solar Energy, in Portuguese) will be presented in Part II of this work.

Keywords: GIS, Planning and Management, Photovoltaic Energy, PRODEEM

1. Introduction