Benchmarking is the largest activity within the MESoR project. The aim of the benchmarking exercise is to establish a coherent set of benchmarking rules and reference data sets to enable a transparent and comparable evaluation of the different solar radiation data sources. The rules are developed in conjunction with the IEA Task 36 on “Solar Resource Management” of the Solar Heating and Cooling Implementing Agreement and shall serve as a standard for benchmarking to make results comparable.

Each of the databases analysed here is integrated within a system (software setup) that provides additional tools for search, query, maps display, and calculation of derived parameters. PVGIS (the European section), includes solar radiation database developed by combination of solar radiation model and interpolated ground observations. The datasets Satel-Light and HelioClim-2 (accessible through the SoDa web portal) are built from Meteosat and MSG satellite images, respectively. NASA SSE release 6 (accessible also through RETScreen software) combines results from ISCCP

satellite project with NCAR reanalysis products. Primary data incorporated inMeteonorm version

6.1 and ESRA are developed by interpolation of ground observed data with support of satellite images (MSG and SRB, respectively). In Tab. 1 we summarise the main characteristics of the databases/systems including the quality indicators Root Mean Square Difference (RMSD) and Mean Bias Deviation (MBD).

While NASA, Satel-Light, PVGIS, and partially also Meteonorm systems are available for free, the ESRA, HelioClim-2 and full version of Meteonorm are to be purchased.

Geographical extension of the spatial products differs: from global (NASA and Meteonorm) to cross-continental (HelioClim-2 covering Europe, Africa and Southwest Asia) and European (ESRA, PVGIS and Satel-Light). Here we focus on the subsection of the European continent (Fig. 1) where all the data sources overlap.

2. Method

2.1. Map comparison

Map-based comparison as performed here is a type of relative benchmarking of solar databases. It does not point to the “best” database, but it gives an indication of the user’s uncertainty at any location within the region. As the existing spatial products cover different periods of time, this comparison introduces also uncertainty resulting from the interannual variability of solar radiation. Here we perform a cross-comparison of maps of long-term average of yearly sum of global horizontal irradiation.

The maps from all data providers are harmonised and integrated into a geographical information system (GIS) with latitude/longitude spatial reference. The grid resolution of 5 arc minutes is chosen to provide a representative outlook at the regional (rather than local) differences within the continent. Choosing such a resolution, more detailed features that are present in the databases of HelioClim-2, Satel-Light, PVGIS and Meteonorm are suppressed (smoothed out), but the regional features are well pronounced. Integration of 6 data sources of yearly sums of global horizontal irradiation provides three results:

• Map of overall average gives the user an indication of spatial distribution of solar resource estimated by the simple averaging of the 6 datasets;

• Map of standard deviation provides information on magnitude of differences between the combined data sources, i. e. user’s uncertainty. If we assume that the estimates are normally distributed, from standard deviation a confidence interval can be calculated in which the value falls corresponding to a given probability. For example, a multiple of 1.95996 would give a range where the value from the average map falls with 95% probability.

• Maps of differences between individual databases and the overall average indicate deviation of the values in the particular dataset from the overall average.

A multicomponent solar thermal system was installed in Bishkek to preheat water for a district heating net in the context of a joint research project of Kassel University (Germany) and Kyrgyz State Technical University in Bishkek (Kyrgyzstan). For detailed investigations different parameters including solar radiation are measured since autumn 2004 with very accurate sensors every 15 seconds to generate one-minute mean values. Solar radiation is measured with pyranometer Kipp&Zonen CM11 with an accuracy of 1.5% of the measured values. For some periods, however, the measurement data is missing for different reasons (e. g. technical problems with the sensor power supply unit or no power supply at all). For this study mean values of monthly solar irradiation were generated from the available measurement data for the period 2005 — 2007.

2. Comparison of meteorological data

The focus of this study is to compare values of ambient temperature and solar irradiation from the mentioned sources because these two parameters are the most important for estimation of solar energy gains. The following abbreviations are applied for the sources of meteorological data:

• FrunzeM — measurements from weather station Frunze

• Met 5.1 and Met 6.0 — Meteonorm 5.1 and Meteonorm 6.0 respectively

• MD — own measurement data

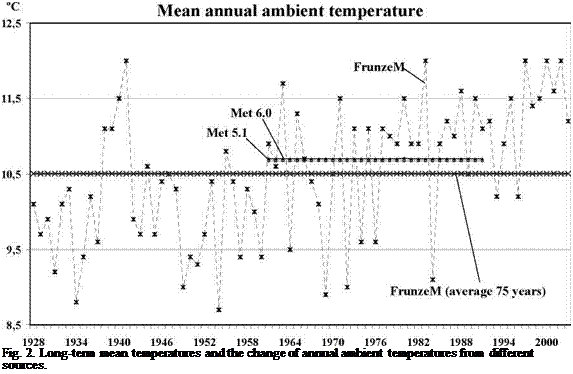A fluctuation of mean annual ambient temperatures measured by the local meteorological station Frunze since 1928 and long term mean ambient temperatures are shown in Fig. 2.

A long term mean temperature from both versions of Meteonorm is about 0.2 K higher than that measured by the station Frunze. The difference results from different periods considered. In Meteonorm a long-term mean ambient temperature is calculated for the period from 1961 till 1990 (30 years), while a mean temperature from the station Frunze is calculated for the period from 1928 till 2003 (75 years). For the same period 1961-1990, mean temperatures from the station Frunze and Meteonorm are in agreement (see Table 1).

A fluctuation of annual global solar irradiation and its mean values from different sources are shown in Fig. 3. The annual global solar irradiation from the station Frunze for the years 2003­2007 is estimated from 6 solar radiation measurements per day (see section 2.1).

Annual global solar irradiation from own measurements («1500 kWh/m2a) and the weather station Frunze (1572 kWh/m2a) are in a good agreement, while its values from Meteonorm 5.1 and 6.0 are approx. 20% lower (see Fig. 3) and even out of the fluctuation range.

As shown in Fig. 4, the solar irradiation from Meteonorm and other sources are in a good agreement in winter. In the period March — September the monthly diffuse solar irradiation values generated with Meteonorm are higher than the measured values, which leads to lower global solar irradiation values. The higher values of diffuse solar irradiation in Meteonorm are probably caused

by admitting higher cloudiness or air pollution. Furthermore, the concavity in summer of the monthly global solar irradiation generated with Meteonorm 5.1 is not typical for a continental climate. It is also inconsistent with the monthly sunshine duration for Bishkek (see Fig. 5), which has no concavity or only one maximum point.

Sunshine duration

If the latitude of Bishkek in Meteonorm 6.0 is changed from 42.8°N to 42.2°N, annual global irradiation increases to 1466 kWh/m2a (+20%) and annual diffuse irradiation decreases to

618 kWh/m2a (-7%). Thus, the radiation data for 42.2°N latitude is in the same range with the measurement data from the local weather station Frunze and the research project (MD). The same tendency occurs if the latitude of Bishkek is changed from 42.8°N to 43.4°N (1468 and 625 kWh/m2a or +20% and -6% respectively). This high change in the radiation data for a little change in the location is probably caused by the interpolation method of Meteonorm.

°C

13.5

13

12.5 12

11.5 11

10.5 10

9.5 9

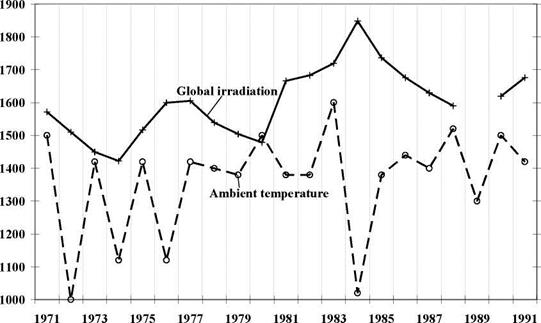
As shown in Fig. 6, the annual global solar irradiation and the mean annual ambient temperature measured at the weather station Frunze in the period 1970 — 1991 are not positively correlated. The seasons (summer, autumn, winter, spring) and single months have the same tendency. The reason is that the weather and the ambient temperature in Kyrgyzstan are influenced not only by solar radiation but also by 17 weather processes [5], e. g. Siberian anticyclone brings cold air from Siberia.

3. Conclusion

Solar radiation and ambient temperature data from different sources (a local weather station, Meteonorm 5.1 and 6.0 and own measurements) have been compared with each other for Bishkek, Kyrgyzstan in this study. It was identified that the altitude of Bishkek city in Meteonorm is wrongly defined (2111 m instead of 760 m), which leads to significantly lower ambient temperatures. Therefore, it is necessary to define Bishkek manually as a new site with the correct coordinates. In this case the ambient temperatures are in agreement with those measured by the weather station Frunze.

Annual global solar irradiation from own measurements (1500 kWh/m2a) and weather station Frunze (1572 kWh/m2a) are in a good agreement, while its values from Meteonorm 5.1 and 6.0 are approx. 20% lower. Correspondingly, the ratio of the direct and diffuse solar irradiation is much lower in the Meteonorm data (approx. 1) than in the weather station Frunze data and own

measurement data (approx. 2). Furthermore, monthly sums of global solar irradiation generated with Meteonorm 5.1 have an untypical trend in summer, having two local maximum points. This is inconsistent with irradiation data from other sources and with the sunshine duration in the relevant period.

Such differences in solar radiation data can lead to significantly different solar gain predictions, especially if the solar irradiation on a tilted surface shall be calculated. Thus, the source of meteorological data shall be carefully selected. For sites, close to weather stations with relevant data available in the Meteonorm database, data generated with Meteonorm can be applied. If no weather station with relevant data close to the desired site available in Meteonorm database, other sources should be considered too, e. g. satellite-derived radiation rata, local meteorological stations or own measurements. In both cases, the data from Meteonorm should be proved on plausibility, particularly for sites or stations in developing countries.

Acknowledgements

The authors would like to express their gratitude to the Volkswagen Foundation, Germany for the financial support of the research project and the Central administrative board on hydrometeorology of Ministry of Emergency Measures of the Kyrgyz Republic for providing the meteorological data from the weather station “Frunze”.

References

[1] John A. Duffie, William A. Beckman, Solar Engineering of thermal processes, John Wiley & Sons, Inc., Hoboken, New Jersey, 2006

[2] J. C.McVeigh, Sun Power: an introduction to the Applications of Solar Energy, translated by Guhman G. A., Moscow Energoisdat, 1981

[3] Reference book on USSR climate, Leningrad 1989

[4] Handbook for hydro meteorological station on solar radiometry, Leningrad 1971

[5] Pavlova I. A., Changeability of synoptic processes in Kyrgyzstan, Metrology and Hydrology in Kyrgyzstan 2001

[6] Handbook Meteonorm 5.1

[7] Handbook Meteonorm 6.0

[8] E. Frank, K. Vajen, A. Obozov, V. Borodin (2006): Preheating for a District Heating Net with a Multicomponent Solar Thermal System, Proc. EuroSun 2006, Glasgow

[1] Introduction

Electric shower heads are presently installed in 73.1 % of the Brazilian houses. These devices accounts for around 60 % of the peak load in between 6:00 p. m. and 8:00 p. m., as is shown by reports of the Brazilian electric power system [1]. As demonstrated in a large scale experiment [2], Compact Solar Domestic Hot Water Systems (CSDHWS), conjugated to electric shower heads, are able to reduce the mentioned peak load due to shower heads by around 60 %. However the peak is expected to remain unchanged for those days of low solar radiation incidence. To further increase the peak power reduction and its confidence, an intelligent compact solar domestic hot water systems is under development and first simulation and optimization were carried out in [3] and [4]. According to the proposed system preheating by auxiliary energy should be done in order to provide preheated water at 6:00 a. m. and a specified storage water temperature at 6:00 p. m. Thus the preheating energy depends on daily available solar energy. Apart from the features solar energy use and peak reduction, additional advantage of this system is obtained by heating the water of the

[2] www. meteonorm. com

Frank Bason

SolData Instruments, Linabakken 13, DK-8600 Silkeborg, Denmark
Corresponding Author, soldata@soldata. dk

Abstract

The data collection phase of the Danish Galathea III Expedition was conducted from August 2006 until April 2007 [1]. During this period the research vessel Vmdderen undertook a round the world voyage of nearly 100.000 kilometers while acting as a platform for scientific research in a range of disciplines. The researchers and instruments aboard the ship collected data from many locations around the world from 66.90 N to 67.50 S latitude. Among the experiments aboard the ship was an optics table sponsored by SolData Instruments and containing among other instrumentation three pyranometers for continuous measurement of global solar irradiance on a horizontal surface [2]. Knowledge of global solar irradiance is important for studies of the atmosphere and solar radiation and consequently for modeling the evolution of the Earth’s climate. We employ the Linke turbidity factor in our analysis, for this parameter is often referred to in the literature of atmospheric physics [3].

Keywords: Galathea Expedition, Linke turbidity factor, solar irradiance

1. Introduction

The purpose of this paper is to present an analysis of the global irradiance measurements. In particular we will focus on the computation of Linke’s turbidity factor TL at a wide range of locations and the implications of these results for a general description of solar resources around the world. The factor TL is closely related to the transmittance of the atmosphere on clear days [4]. As a general rule the atmosphere is clearer at higher latitudes, and the large amount of data available from the expedition has permitted the development of an algorithm to describe this relationship. Among the useful results obtained is a correlation between the Linke turbidity factor and the latitude. Secondary parameters such as the surface air water vapor content are also examined.

The turbidity factor was obtained from the horizontal radiation data using an incident direct plus diffuse rad­iation model, observed values of the solar irradiance and a numerical algorithm to determine TL. Based on these results it is possible to provide a highly realistic prediction of the global irradiance on a clear day in a maritime environment. The model developed also supplies information about the distribution of diffuse and direct irradiance, information which is important for the design of solar energy systems. Furthermore TL has implications for atmospheric visibility.

1.1. Information of stations

The global solar radiation and sunshine duration data during the period from 1994 to 2003 reported in this paper were provided by the China Meteorological Administration (CMA). Professor Tien Shengyuan has divided climatic zone of China into eight large-scale climatic zones, and he also has advanced the representative city for every climatic zone in the year of 1989. The information of these cities is as follows [3]

By convolution, the length of the scaled and translated wavelet functions in the DWT is distinct from the signal length, which can lead to additional convolution uncertainties on the boundaries of the signal as stated in [19]. The authors of paper [9], as well as a large number of references which using the orthogonal DWT as auxiliary tool to obtain performance improvement of Time Series Prediction (TSP) models, do not consider that its obtained performance may not hold for the operation of the prediction model. The documented uncertainty may increase during the application of the model to predict unknown future values in real or actual time. The authors applying the TSP models to the vector of the training and the validation set in which the increased boundary uncertainty do only appear on the correction of the last predicted value of these vectors. Some authors applying padding techniques to the orthogonal DWT, which reduce the uncertainties of the reconstructed signal at the signal boundaries. These techniques distort the typical characteristics of the wavelet coefficients and the behavior of the sub-signals at the boundaries to lower the reconstruction uncertainty at the boundary. As the wavelet sub-signals (see section 3.1) are used for the time series prediction models, the local distortion can decrease its performances considerably. Therefore, also the performances of the reconstructed predictions decrease. Furthermore, most of the authors do not consider that if the trained and validated TSP model is applied for the prediction, it is continuously exposed to boundary conditions. At each new prediction, the model input variables or predictors are separated from the estimated output variable, by the right hand side boundary of the sub-signals as also discussed in Renaud [23]. The boundary appears new, because the signal has to be decomposed before each new prediction. By the utilization of wavelet networks as presented in [7] and [8] the boundary uncertainty in time series predictions may not appear due to its adaptive learning feature which can be applied to real time predictions as worked out in [24]. Wavelet networks substitute the sigmoidal activation function by a wavelet function. However, this method presents too many permutations for its optimization due to the selection of the network architecture, the number of neurons in the network layer, the wavelets functions and its scaling and translating counterpart, thus its optimization is a time consuming computational task. The anti-symmetric Haar was used in [23] for time series
predictions. Beside the Haar wavelet the DWT provides also the biorthogonal wavelet functions for the symmetric wavelet transform. The statistical correction in the present article is based on a biorthogonal wavelet function. Due to its symmetry and linear phase characteristic undesirable phase distortions of the sub-signals are avoided [25] and boundary treatment can be simplified [19]. By symmetric padding at the boundaries the bi-orthogonal wavelet transform, is converted in a DWT on a bounded interval as exposed in [26].

The region of the study is the area of Andalusia, in the southern part of Iberian Peninsula (Figure 1), covering around 87.000 km2. The region is located in the transition zone from middle latitudes to subtropical climates (latitudes 35° 30′ to 38° 30′ N and longitudes 7° 30′ to 1° 30 W), with the Atlantic Ocean and the Mediterranean region in the southern bound.

2.1. Dataset

The experimental dataset used in the study includes four year (2003-2006) of daily global radiation in the horizontal surface values, measured at 166 meteorological stations along the study region.

The stations are owned and maintained by the Andalusia Regional Government, and are part of the Agricultural and Environmental monitoring network. The location of the station, displayed in Figure 2, covers almost homogeneously the region. The 166 stations were divided into two groups: two-third of the stations (112) was used to train the models (training dataset) and one-third (54) was used for the validation process (validation dataset). Both groups were selected trying to cover homogenously the study region.

The calculation of the direct normal irradiance is performed in different steps. In a first step cloud information is derived from the satellite measurements using an enhanced version of the Heliosat method [1]. As a measure of cloudiness a dimensionless clear sky index k* is derived. Using a clear sky model the global irradiance is immediately related to the clear sky index, while our new beam fraction model allows for calculating the DNI. Fig. 1 represents the necessary process steps, which are described in this section.

The model HELIOSAT-2 arises as a natural evolution of the model called HELIOSAT developed by Cano and Diabate during the 80s. The progress introduced in this model corresponds to modifications on the model of clear sky used by means of the introduction of some descriptive parameter of the atmospheric quality. In both models estimation of a dimensionless parameter (n), called cloud index, is proposed on a basis of using the brilliance detected by the satellite.

The cloud index is estimated for every pixel of the image according to so called apparent or

instantaneous albedo (p ), albedo of the clouds (Pn) and ground albedo (pg) as shown in the following expression:

n = (p‘ — Pg ){p’n — Pg )1 (1)

The evaluation of the different albedos necessary for the calculation of the cloud index is obtained from the radiance (L), the geographical parameters that define the pixel in question (latitude, length and altitude) and the information about the atmospheric local quality contained in the coefficient of atmospheric turbidity of Linke (TL).

To conclude, the model HELIOSAT-2 calculates the global horizontal irradiance by means of a relation between the so called clear sky index Kc (global / global of clear sky), and the cloud index (n). The relation used in this work is a modification of the original proposal in which the local median of the cloud index is used [5]. So that the global irradiance estimated in every pixel can be calculated as:

G=KcGcs (2)

where GCs is the global irradiance of clear sky calculated by the ESRA [6] algorithm. The final daily irradiation is calculated by integration of the different images available in a day.

This activity focuses on collection of high quality ground measurements which can be used as a reference in the benchmarking exercises. The measurements should be conducted with high accuracy, high frequency and traceable maintenance of the equipment. Data has been collected from the Baseline surface radiation network (BSRN), International Daylight Measurement programme (IDMP), the meteomedia network, the World Radiation Data Center (WRDC) and the Global Atmospheric Watch (GAW) programme. In addition further measurements were collected from scientific institutions, providing they fulfil the quality criteria above.

A common quality control procedure has been defined for all broadband time series data. The parameters for the quality assessment have been deducted from the Baseline Surface Radiation Network Operation Manual [3] and operational experience of the partners involved. All data is flagged if:

• It is within the physical possible limits. The applied physical limits are shown in table 1.

• It is lower than it would be in a dry and clean atmosphere. We apply the e. g. the Bird clear sky model (Model C in [4]) with aerosols and water vapour set to zero.

• The components of direct, diffuse and global parameters are coherent (if all are available). The conditions and limits are described in table 2.

Only values passing all tests will be used in the benchmarking exercises.