The parallel lines in 3D space appear in the image to meet at a point when their plane is not parallel to the image plane (Figure 4). This point of convergence is called the vanishing point and can be used to determine distances in the real world [2]. The vanishing point of lines is sufficient to analyze and detect the edges without the need for completely calibrating the camera used. In the case of the BiFres system, the structure frame of the concentrator is a rectangle with four metal sides. The four corners are easy features to locate from the pictures and their coordinates are used to form the equations of lines. The equations of lines are solved simultaneously to locate their intersection; the vanishing point. With the knowledge of the actual dimensions of the concentrator and their corresponding image pixel counts, a scaling factor is obtained which converts the image pixels to space dimensions. Using triangle similarities, the coordinates of any image point on the reference lines are then directly related to the actual distance Xm. This information is further fed into the geometrical algorithm for the calculation of the real surface slope at the specified point on the mirror. It is important to mention that the above method is an approximation because the mirrors do not lie in the same plane of the concentrator frame; each mirror has a different tilt angle.

However, the effect of this tilt is less apparent because the camera is located at a large distance from the concentrator between 18 to 30 meters away.

6. Results and analysis

The following graphs show the error map of the surface of each mirror as well as the root mean square error for the whole mirror with the concentrator at vertical and inclined positions. Presented here are only the 15 mirrors of the left part of the concentrator.

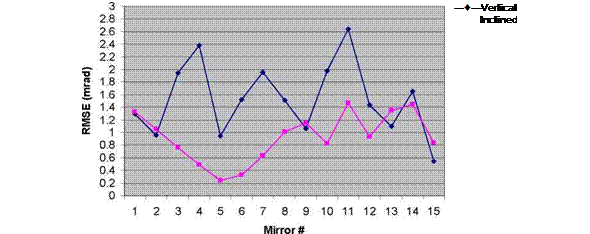The two graphs show that the mirrors at the inclined position posses surface errors within the range of 3 mrad compared to the vertical position that shows errors up to 4.5 mrad. In the vertical position, RMS errors are between 0.54 and 2.63 mrad while in the inclined position they are between 0.23 and 1.46 mrad. These values are within the range of RMSE and comply with surface errors quoted for other concentrator systems [1, 4, 10]. The results contradict the expectations that at inclined positions the RMSE should be higher than that at the vertical position due to the mirrors bending under their own weight. The reason for this is that during tracking, the motor exerts a lot of power to retain the concentrator to its horizontal position. The motor moves slower than usual and this affects the tracking precision. Therefore a heavy counter balance is attached to the concentrator frame to help the motor during its movement. The balance is made of heavy iron bars connected to centre body of the concentrator and balanced with cable wires to the corners of the structure. In the vertical position, the bars are perpendicular to the frame and parallel to the ground. At this position the cable wires are at their highest tension and exert stresses on the structure and consequently the mirrors holders. On the other hand, when the concentrator is at an angle, the bars exert less torque on the structure and the overall effect on the mirrors is less pronounced.

7. Conclusion

The absorber reflection method has been used to assess the surface slope errors of a linear Fresnel PV/T concentrator. The absorber reflection method has proved to be an effective and simple tool to obtain slope error map of reflecting concentrating systems. Results show that mechanical stresses on the structure, where mirrors are attached, play an important role in the errors. Structure manufacturing should be precise because mirror misalignments can cause the reflected rays to be blocked by the preceding mirror thus increasing the non-uniform illumination and shading effects on the modules. The counter balance should be redesigned to avoid its negative implications. The experiment has shown that the accuracy in locating the camera is a crucial point for the reliability and accuracy of the measurements.

8. Acknowledgments

This work has been supported by the 6th European Union Research Programme’s Marie-Curie early

stage research training network “Advanced solar heating and cooling for buildings — SOLNET”.

References

[1] J. Coventry (2004), A solar concentrating photovoltaic / thermal collector. PhD thesis. Australian National University

[2] H. Doehler, B. Korn, Robust position estimation using images from an uncalibrated camera. Digital

Avionics Systems Conference, 2003. DASC ’03. The 22nd Volume 2, 12-16 Oct. 2003. Pages:9.D.2-9.1-7

[3] E. T Franklin, J. S. Coventry, Effects of highly non-uniform illumination distribution on electrical performance of solar cells. Proceedings of Solar 2002 — Australian and New Zealand Solar Energy Society

[4] S. A. Jones, J. K. Gruetzner, R. M. Houser, R. M. Edgar, T. J. Wendelin, VSHOT: a tool for characterizing large, imprecise reflectors. Annual international symposium on optical science, engineering, and instrum­entation, Denver, Colorado USA, November 1996. Department of Energy

[5] S. Kammel, F. P. Leon, Deflectometric measurement of specular surfaces. Instrumentation and Measurement (2008), IEEE Transactions 57, pp. 763-769.

[6] M. C. Knauer, J. Kaminski, G. Hausler, Phase measuring deflectometry: a new approach to measure specular free-form surfaces. Optical Metrology in Production Engineering. Proceedings of the SPIE (2004), volume 5457, pp. 366-376

[7] K. Pottler, E. Lupfert, G. Johnston, M. Shortis, Photogrammetry: A powerful tool for geometric analysis of solar concentrators and their components. Journal of Solar Energy Engineering (2005). 127, pp. 94-101.

[8] M. R. Shortis, G. Johnston, Photogrammetry: An available surface characterization tool for solar concentrators, Part II Assessment of surfaces. Journal of Solar Energy Engineering (1997). 119, pp. 286­291

[9] M. R. Shortis, G. Johnston, Photogrammetry: an available surface characterisation tool for solar concentrators — Part I: measurement of surfaces. Journal of Solar Engineering (1995). 118 (3), pp. 146-150.

[10] S. Ulmer, B. Heinz, K. Pottler, E. Lupfert, Slope error measurements of parabolic troughs using the reflected image of the absorber tube. 13th International Symposium on concentrating solar power and chemical energy technology: SolarPaces. Seville, Spain. June 20-23, 2006.

[11] T. Wendelin, K. May, R. Gee, Video scanning Hartmann optical testing of state-of-the-art parabolic trough concentrator. Solar 2006 Conference (ISEC’06).July 8-13, 2006.Denver, Colorado USA

[12] T. Wendelin, Parabolic trough optical characterization at the National Renewable Energy Laboratory. 2004 DOE Solar Energy Technologies Program Review Meeting October 25-28, 2004 Denver,

Colorado

[13] T. Wendelin, G. J. Jorgensen, R. L. Wood, SHOT: A method for characterizing the surface figure and optical performance of point focus solar concentrators. In: Solar Engineering. American Society of Mechanical Engineers, New York, (1991) pp. 555-560.

The experiment was conducted in the solar calorimetry laboratory. The tests were carried out in an air — conditioned room having an average temperature of 23°C. Figure 4 shows the pictures of the experimental test rig, while figure 5 shows the PIV system.

Conserval Engineering Inc., 200 Wildcat Road, Toronto Ontario Canada M3J 2N5
Corresponding Author, ihollick@solarwall. com

Abstract

Canada’s National Solar Test Facility and the Danish Technological Institute have completed testing of PV Thermal modules as part of the International Energy Agency Task 35 Project. The data shows that it is possible to capture two to three times more thermal energy than electricity from a PV array. Panels from various manufacturers were tested under NOCT conditions, and the results showed that when PV modules were mounted on top of SolarWall® transpired collector panels, the total solar efficiency was in the 25% to 50% range depending on the PV module tested, compared to the typical 6 to 12% for PV modules alone.

By removing the excess heat generated by the PV modules, the electrical output is increased. Modules can commonly operate at temperatures over 50 degrees above ambient temperature resulting in a performance reduction of more than 25%. By removing the heat from the module and lowering the operating temperature, significant gains can be made in system performance and the heat can be utilized for practical heating purposes. The economics of a PV system that incorporates a thermal component can also be improved on buildings where the PV heat can be used to displace space heating energy.

Keywords: PV thermal, transpired collector, BIPV

1. Introduction

The trend with photovoltaic (PV) installations is towards building integrated systems, and while this is advantageous in many regards, there are problems associated with conventional methods of integrating PV directly into a building.

The main problem with building integrated photovoltaic (BIPV) systems is heat retention under the PV modules. The heat produced can be as much as 50°K (90°F) over ambient temperature resulting in two concerns. The first is the possible structural damage from heat if panels are not vented or if heat is not recovered. The second is the lower efficiency of most PV modules with increasing temperature. Crystalline cells are affected by temperature and the performance drops as cell temperature rises. It has been shown that for each °C increase in temperature, the power production drops by ~0.5%. This means that a BIPV 100 W crystalline module at 65°C is only delivering 80 W of power compared with the 25°C name plate rating.

A PV module operating at its stagnation temperature of 50°K above ambient, when the heat is not removed and if ambient temperature is 30°C, will experience a module temperature of 80°C, or even higher, on some tiled roofs.

Another issue facing installers and customers is competition for roof space and deciding on which solar technology should have priority. Covering a roof with PV modules only uses 10% to 15% of available solar energy and eliminates the possibility for future solar thermal systems with much

higher solar conversion efficiencies. A client may not be able to install solar panels to heat water, a pool or the building when the roof is already covered with a solar electric technology.

Grid tied PV systems have a high initial cost and are generally sold only with generous incentive programs. A possible solution to the long payback situation is to see whether the "waste" solar heat can be recovered and used to lower heating costs.

1.1. Goals

The just described experience demonstrates that a deep attention has to be paid in planning SHC-CHP systems from three points of view: layout, control strategy and machine sizes. The present research work proposes a first layout with a specific control strategy and a procedure for sizing such a plant with the main goal to avoid issues like the above mentioned. The selected plant configuration is then simulated in TRNSYS along one year to analyse the off-design behaviour of the single components, their interaction and the performance of the overall system.

1.2. Major hypothesis

The selected layout and the sizing procedure have been applied supposing the EURAC building to be the final user. In this regard, data derived from the installed monitoring system have been used. These data correspond to the building heating and cooling demand monitored since November 2005 to

October 2006 (Fig. 3.). To simulate the power load, the temperatures of the stream being delivered to the building and returning from it have been assumed constant, both in winter and in summer, according to the selected distribution system (DS). Thus, the demanded power has been translated in a “demanded mass flow” at constant temperature gaps. So, during the simulations, the “demanded mass flow” at the assumed return temperature gets elaborated by the designed facility. Under the mentioned hypothesis, checking that what is produced by the facility matches what is required by the building means ensuring that the “demanded mass flow” gets distributed at the assumed delivery temperature.

Henrik Davidsson*, Bengt Perers, Bjorn Karlsson

Energy and BuildingDesign, Lund University, B. O Box 118, SE 221 00 Lund, Sweden
Corresponding Author, henrik. davidsson@ebd. lth. se
Abstract

A building-integrated multifunctional PV/T collector have been developed and evaluated. The PV/T solar window is constructed of PV cells laminated on solar absorbers and is placed in a window behind the glazing. To reduce the costs of the solar electricity, reflectors have been introduced in the construction to focus radiation onto the solar cells. The tiltable reflectors render a possibility to control the amount of radiation transmitted into the building. The insulated reflectors also reduce the thermal losses through the window. A model for simulation of the electric and hot water production was developed. The model can perform yearly energy simulations where different effects such as shading of the cells or effects of the glazing can be included or excluded. The simulation can be run with the reflectors in an active, up right, position or with the reflectors in a passive, horizontal, position. The simulation program was calibrated against measurements on a prototype solar window placed in Lund in the south of Sweden and against a solar window built into a single family house, Solgarden, in Alvkarleo in the middle of Sweden. The results from the simulation shows that the solar window produces about 56% more electric energy per unit cell area compared to a vertical flat PV module.

Keywords: solar window, PV/T

1. Introduction

A diversity of technical solutions needs to be applied and developed if solar electricity is to become cheap enough to compete with grid electricity. One technique for reducing the price of solar electricity is to use the reflector to focus radiation onto the PV cells, thus allowing expensive PV cells to be replaced by considerably cheaper reflector material. Active water cooling on the back side of the cell gives both relatively cold, high efficient cells, and hot water for domestic use. Further price reduction is possible if the solar modules can be integrated into the building construction. Integration makes it possible to use existing frames and glazing for the solar modules or, alternatively, to replace roofing materials and windows by solar modules. Wall integrated solar collectors using reflectors have been shown to increase the electrical output substantially [1] compared to flat vertical PV modules. All these technologies have been combined in the PV/T hybrid technology presented in this work.

A building integrated multifunctional solar window was proposed and developed by Fieber [2]. The solar window, se figure 1, is constructed of absorbers on which the PV cells have been laminated. The solar window is building-integrated into the inside of a standard window, thus saving frames and glazing and lowering the total price of the construction. In order to minimize the PV cell area, reflectors have been placed behind the absorber. When tilting the foldable reflectors to a vertical position the solar radiation is focused onto the absorbers. When the reflectors are tilted to a horizontal position the solar radiation is let into the building to allow for passive heating. This means that the

reflectors in a closed position increase the radiation on the cells, reduce the thermal losses through the window and also work as a sun shade. The glazing of the window in front of the absorbers is anti reflection treated to maximize the transmittance.

2.1. Geometry

The geometry of the solar window is shown in figure 1 above. The optical axis, v, of the parabolic reflector is directed 15° above the horizon with focus on the front edge of the absorber. This means that all radiation from 15° and higher solar altitudes will hit on the absorber between the focal point, F, and the reflector. The focal length is denoted p, the height of the glazing h and a is the absorber width. The angle w is the angle between the glazing and the absorber plane and qNS is the incident angle of the solar radiation projected in the north-south vertical plane. The absorbers are 1.11 m long and 8 cm wide, and the PV cells are 12.5 cm * 6.25 cm. The solar window in Solgarden is constructed of 8 absorbers per window unit, and the prototype solar window is constructed of 5 absorbers, see figure 2. The Solgarden solar window has 64 PV cells in series and the prototype solar window has 8 PV cells in series. The total window area is 16 m2 in Solgarden and about 1.2 m2 for the prototype solar window.

The reflector parabola is described in Eq. (1). r is a vector from F to a point on the parabola at angle ф.

г(ф) = p/cos2^) (1)

Both h and a can be expressed by r for the two angles w=105° and u+v=35°, respectively for the solar window. The ratio between h and a, which is defined as the geometrical concentration factor, can be calculated to be 2.45 for the construction.

The architectural implication such as light distribution has been investigated [2]. Following this, long term measurements were performed regarding energy production, both electrical and hot water. This was carried out on a prototype solar window placed in Lund in the south of Sweden as well as from a solar window built into a residential building in Alvkarleo about 100 km north of Stockholm, Sweden.

In this paper, we describe a model developed to simulate the yearly energy production of the hybrid window system from climatic data. The model uses both experimentally measured parameters and theoretically derived values and functions in the calculations. It takes into account shading caused by the window frames and also includes the transmittance through the glazing and the angular dependence of the PV cells. The model also allows for analyzing different limiting effects such as shading or transmittance through the glazing. This makes it possible to study the potential of development for the solar window.

Method

Measurements of the performance of the multifunctional PV/T hybrid solar window were carried out during 2006 on a prototype solar window placed in Lund, Sweden (55.44N, 13.12E). A full scale system combining 4 of these solar windows, another 4 is planed, was installed in a single family home called Solgarden in Alvkarleo, Sweden (60,57N, 17,45E) and evaluated during 2006-2008. The window was directed 23° towards east. The solar windows can be seen in figure 2. The measurements of the generated current and voltage produced by the prototype solar window were carried out using a Campbell CR1000. The radiation, temperatures and water flow through the absorbers was measured using a Campbell CR10 logger. The temperature measurements were carried out using PT100 sensors. All measurements made in Solgarden used a Campbell CR10. Measurements were monitored both with the reflectors in a horizontal and in a vertical position. The prototype solar window was supplied with water of constant inlet temperatures and the measurements were carried out during both day and night. Night time data were used for determining the thermal losses of the window.

A simulation model was developed to evaluate the solar window. The model uses the direct and diffuse radiation together with the inlet water temperature, the ambient temperature and the time, and thus the solar angles, as inputs. The outputs are thermal and electrical delivered power. In order to simplify the calculations the power delivered by the solar window was divided into three components, Pdirect,

Preflector, and Pdiffuse. The first is Pdirect, power caused by the direct radiation that hits the absorber directly, the second component is Preflector, power caused by the direct radiation that goes via the reflector. The third component, Pdiffuse, is the power contribution caused by the diffuse radiation. Figure

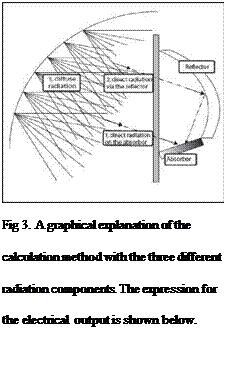3 graphically explains the three different components of radiation. Ptotal is the total power delivered by the window.

Pdirect=Ib*Tglass(©1)* Opv(©2)*fshading(©3)*ACell*npv *^(©2) (2)

Preflector Ib *Tglass(©1)* apv(©4)*freflector(©5)*Areflector*npv*Rreflector*cos(©5) (3)

Pdiffuse= Idiffuse *C1,2 (4)

Ptotal= Pdirect+Preflector+ Pdiffuse (5)

Ib and Idiffuse are the beam radiation and the diffuse radiation against the window. Tglass describes the angular dependent transmittance through the glazing; apv describes the angular dependence of the absorptance of the PV cells, and fshading describes the shading of the PV cells caused by the window frame. freflector is a correction factor for the shadow effects for the radiation which is reflected. This function includes the shading of the reflector. The angles ©1 to ©5 are the different incidence angles for the beam towards the components of the solar window. Acell and Areflector are the areas of the PV cell and the reflector, respectively. npv and Rrefiector are the efficiency of the solar cells and the reflectance of the reflector. C12 is a response function for the diffuse radiation obtained from measurements during cloudy days, when the beam radiation has negligible influence on the performance. Measurements during cloudy days were performed with the reflector in both horizontal and in vertical positions, allowing both C1, horizontal reflector and C2, vertical reflector, to be determined. The transmittance, Tglass, through the window was calculated using Fresnel’s equations and Snell’s law. The shading factors fshading and freflector were calculated theoretically from the PV/T window geometry. A measurement was performed to determine apv, the angular dependence of the PV cells.

In order to calculate the thermal output a fourth term has to be added to describe the thermal losses in the absorber. The thermal losses, Pthermal loss prototype for the prototype solar window and the thermal

losses Pthermal loss Solgarden is shown below.

Since the solar window in Solgarden experiences thermal losses to two different temperatures, the ambient temperature and the indoor temperature, two different U-values where used. The Usolgarden out is the thermal loss to the outside and the Usolgarden in is the thermal loss to the inside. Awindow is the total window area. DeltaT out is the temperature difference between the ambient temperature and average water temperature and DeltaT in is the temperature difference between the indoor temperature and the average water temperature. Uprototype is the U-value for the prototype solar window and DeltaT is the temperature difference between the ambient temperature and the average water temperature.

Result

Two different types of graphs were used to validate the model. The first type is shown in figure 4, where results from measurements and simulations are compared. The short circuit current Isc in the right figure is from a cell placed in the solar window. The days were chosen to illustrate different weather conditions, such as different ambient temperatures and cloudy weather with sunny intervals. The days where also chosen to show different seasons and thus different solar angles.

During the measurements on the prototype solar window two different, not perfectly synchronized, loggers for monitoring the electrical output and the radiation were used. This means that synchronization problems could arise during partly cloudy days. If the electrical output was measured during a cloudless time and the irradiance was measured during a cloudy time the result from the simulation, using the irradiance as input, differs from the measurement. To solve this problem the simulated and the measured output was integrated daily. Then this irregularity will disappear. The result from this analysis is shown below in figure 5 where the integrated daily measured output on the y-axis is plotted against the integrated daily simulated output on the x-axis. A perfect agreement between simulation and measurement would put all the points on the line, x=y. This analysis was performed both for the thermal output, left figure, and the electrical output, right figures. Validation from the prototype solar window is in blue and the validation from Solgarden is in purple. All values have been normalized to the highest output in each series. The correlation is high for all four validations.

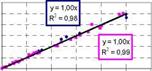
Fig 5. The thermal energy production (left) and the electrical energy production (right). The dots in the graphs
are the integrated daily energy production, the simulated value on the x-axis and the measured value on the y-
axis. The blue dots are from Solgarden and the pink dots are from the prototype window.

Yearly simulations where made for the solar window and for two flat PV-modules. The PV-modules has the same efficiencies and areas as the string module in the solar window but without shading effects and reflectors. The PV-modules are installed on a wall alternatively tilted 20° on a roof. The wall mounted PV module is not shaded like the solar window but still benefits less from the diffuse radiation due to less favourable angles between the cells and the sky. This is also the case for the direct radiation, as can be seen in figure 6. When the PV module is located on a roof at a low tilt it receives more diffuse radiation than a wall mounted PV module since the module can see a larger part of the diffuse sky. This is clearly visible in figure 6. The increase of the electrical output from the direct radiation on the module is due to less loss in the glazing and the possibility for the roof module to utilize the radiation which comes from directions behind the wall. Note that the increase of the diffuse radiation on the roof mounted module almost compensates the reflector contribution on the cells in the solar window. The diffuse irradiation is treated as isotrop.

Fig 6. The annual electrical output from the prototype solar window and from two flat PV-modules on a wall at
90° tilt and on a roof at 20° tilt. In the figure the blue part is electricity produced by the direct radiation that hits
the absorber directly. The red part is the electricity caused by direct radiation that goes via the reflector. The
yellow part is the diffuse radiation that goes directly on the absorber and the light blue is the electricity caused by
the diffuse radiation that goes via the reflector. All results have been normalized to the total annual output from

the solar window.

The same analysis, in this case using TRNSYS, was performed to investigate the thermal properties. A TRNSYS-deck including the solar window or flat solar collectors, pumps, a storage tank, etc and a heating load was constructed. In the simulation all parameters but the areas of the wall collector and the roof collector was kept constant. Figure 7 shows a graph of the area of the flat collector required to

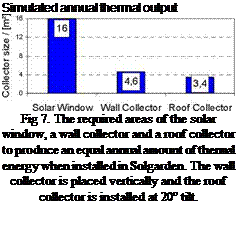
produce the same annual amount of thermal energy as the solar window in Solgarden, turned 23° from south towards east. The roof collector was placed at 20° tilt and the wall collector is placed at 90° tilt to the horizontal. The roof mounted collector can see a larger part of the diffuse sky and has more preferable incidence solar angles and thus gain and produce more energy compared to the wall mounted collector. The absorber area in the solar window is 5.06 m2 and the total window area is 16m2.

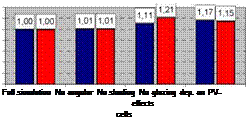
To study the limiting factors in the solar window a simulation was carried out where the factors fglass(©1), fpv(©2) and fshading(03) in Eq. (2,3 and 4) was set to 1, see figure 8. Since the angular dependence of the PV cells is large only for high angles the impact of setting fpv(02) to 1 will be small, the shading is already deteriorating the performance for high solar angles. If the glazing is omitted the yearly electrical output would increase by about 15% and if the shading effects can be removed completely the increase would be as much as 21%. If the shading effect is very large it is better to have one cell less, since large shading is caused by the window frame on the outer cells.

Limiting effects

1,4

1,2

c.

Fig 8. Different limiting factors affecting the solar window. The first bar is the complete simulation. In the
second bar the angular dependence of the PV cells have been removed. In the third bar all shading effects have
been removed and in the last bar the effects from the glazing have been removed. In blue are simulations
performed without the influence of the reflector and in red are simulations including the reflector contribution.

Discussion

The focus of the work in this article is to reduce the total costs of a building including a solar energy system. One solution is to use building integrated PV/T hybrid collectors using reflectors to focus the
radiation onto the absorbers. Different collectors have been proposed [1]. Using such technique fa? ade elements can be saved to reduce the costs. To further develop the building integration technique a multifunctional PV/T hybrid solar window was proposed by Fieber [2]. Integrating the proposed collector into a window saves both frames and glazing. The total price of the construction is reduced further since the concentrating reflectors are tiltable and thus provide flexible solar shading for the building.

The results from the simulation program developed to evaluate the window closely match the measured data. The simulated annual electrical energy production clearly shows the importance of utilizing the diffuse radiation. About 40% of the electrical energy produced in the window is due to diffuse radiation. The comparison performed in Figure 6 shows that the solar window produces about 56% more electrical energy per unit area of PV cells compared to a flat PV module placed on a wall at a 90° tilt. However the roof mounted PV module performs about 2% better per unit area than the solar window. The roof mounted PV module receives more diffuse radiation than the wall mounted system, and thus produces more electrical energy.

The simulation presented in figure 7 shows that the solar window produces less thermal energy per absorber area compared to a flat vertical solar collector or a roof collector installed at 20° tilt to the horizontal. Due to the complex design of the solar window the U-value of the collector is relatively high. The thermal losses from the solar window collector is approximately 50% larger compared to a normal plat solar collector. However, a large part of the thermal losses will heat the building passively. This positive effect is not included in the values in figure 7. A full investigation including the passive effects, such as passive heating of the building due to thermal losses from the collector and taking into account the decrease of passive heating through the windows due to solar radiation utilized in the collector instead of the passive heating, will be presented in future papers.

The results presented in Figure 8 clearly show the importance of choosing the best available glazing for the window. The importance of avoiding shading caused by the frames of the window is also clear. If the shading is extensive it is better to have one less PV cell per absorber. Heavy shading can occur if the cells on the outer edges are placed too close to the window frame. The angular dependence of PV cells is only apparent for large incident angles, and large incident angles are already heavily shaded by the frames and heavily suppressed by low transmission through the glazing. The annual performance can be increased by up to 30% if the impact of shading and angular effects is minimized.

As can be seen in figure 6 it is possible to run simulations with the reflectors in both active, vertical, or passive, horizontal, positions. This keeps the simulation realistic by allowing control mechanisms, based on human behaviour, to decide whether or not to have closed reflectors. For instance there is a possibility to cool the building at night by simply opening the reflectors and thus increasing the U — value of the window. This is not a possibility for a standard window with low U-value.

References

[1] H Gajbert et al, Solar Energy Materials & Solar Cells 91 (2007) 1788-1799

[2] A Fieber, Building Integration of Solar Energy, Lic. Thesis (2005) Report EBD-T—05/3

1.1. General specifications

The PVT system modelled uses air as the heat transfer fluid, drawn through a duct at the rear of the PV modules, and has a glass cover. In winter, air is drawn past the rear of the photovoltaic panels and ventilated into the house. In summer, it is envisaged that air would be drawn in from underground using an air/earth heat exchanger and the heated outlet air would be ventilated to the outside, however, this is not investigated here. Such an earth/air heat exchanger would also be used during winter. In this modelling only the household heating was examined and for simplicity the outdoor air was used as the inlet air for the PVT system.

The example house used for modelling is an existing 100m2 single storey three bedroom house located in Sydney for which the floor plans and building construction details were obtained. This house was modelled with two zones (a north and a south facing zone) and internal thermal mass in which the heat delivered by the PVT system during the day would be stored for release overnight. The house is reverse brick veneer construction with standard brick forming the internal wall layer, followed by 20cm bulk insulation and external cladding giving an R-value of 5 m2K/W. The windows used for modelling were double glazed with a low emissivity coating giving an R-value of 0.5 m2K/W. The roofing material was steel and the ceiling was also insulated with 20cm of bulk insulation to an R-value of 4.5 m2K/W. A timber floor is suspended above an enclosed crawlspace and is insulated with 12cm of bulk insulation to an R-value of 3 m2K/W.

T. P. Fluri1* and T. W. von Backstrom1

1 Department of Mechanical and Mechatronic Engineering
University of Stellenbosch, Private Bag X1, Matieland 7602, South Africa
* Corresponding Author, fluri@sun. ac. za

Abstract

Various layouts and configurations have been proposed for the power conversion unit (PCU) of solar chimney power plants. However, no method was available to make an informed decision on which layout/configuration to choose. The aim of this paper is to present such a method and apply it to several plant configurations. It is found that PCUs with a multiple horizontal axis turbine configuration using a single rotor layout with inlet guide vanes provide the lowest cost of electricity. It has further been found that while the size and performance of the different plants vary a lot, the optimal PCUs all look very similar. The optimal number of turbines varies, but their individual size, the number of blades and even the efficiency of the PCU remain close to constant. The cost of the PCU, however, varies significantly; the specific initial cost of the PCU varies between 437 and 1644€/kW.

Keywords: Solar chimney power plant (SCPP); Cost optimization; Turbine

1. Introduction

Results from pilot plant testing in Manzanares and from various mathematical models found in the literature make large-scale solar chimney power plants a promising option for sustainable power generation [1, 2, 3]. Various layouts and configurations have been proposed for the power conversion unit (PCU) of this power plant concept; layouts with counter rotating turbines or single rotor turbines, layouts with or without inlet guide vanes (IGVs), configurations with single or multiple vertical axis turbines located in the chimney as well as configurations with multiple horizontal axis turbines located on the ground around the chimney [1, 5]. In this paper a method is described, which helps to make an informed decision on which layout/configuration to choose to minimize the cost of electricity (COE). The described method is then applied to several plant configurations. It was developed as part of the PhD dissertation of one of the authors. For more detailed explanations refer to the dissertation [6].

2. Method

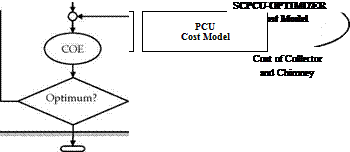
The cost of electricity has been chosen as the main evaluation metric. The structure of the optimization tool, which has been implemented in Matlab, is summarized in the flow chart in Figure 1. The various elements of this optimization tool are described in this section.

The plant performance data are taken from simulation results using the models and the simulation program of Pretorius [2]. The simulation program solves the thermo-flow field in the collector and the chimney of a solar chimney power plant. Conservation equations for mass, momentum and energy are solved simultaneously using finite difference methods. Meteorological data for Sishen, South Africa; (latitude: 27.67° South; longitude: 23.00° East) are used as input to the program. The

(^SCPP

Fig. 1. Flow chart summarizing the structure of the solar chimney power conversion unit optimization tool.

impact of the chimney shadow and all frictional, inlet, outlet, support and heat losses are taken into account. For the power conversion unit an efficiency of 80 % was assumed. Sandstone has been assumed as the ground material. A dry adiabatic lapse rate has been assumed for the vertical temperature profile inside and outside the chimney. Wind effects have been disregarded.

For the present study the flow conditions at the inlet and outlet of the PCU, which have been extracted from the results of this plant performance simulations, are used as input for the PCU optimization. The simple assumption of a constant PCU efficiency of 80 % is replaced by an analytical model, which evaluates the efficiency of the PCU at the different operating conditions taking the efficiencies of the various components of the PCU into account [7].

To allow for the variation in chimney geometry, a parametric chimney cost model is employed. According to Bernardes [4], the surface area specific chimney cost, b, can be approximated as a function of the chimney height, Hc, and the chimney diameter, dc. His Equation 3-4 is used and reiterated here for convenience:

b [€/m2] = 35.39+0.2315 Hc — 0.1223 dc (1)

Note, however, that this approximation for area specific chimney cost should be scrutinized in future work: as curvature and its positive effect on stability decreases with chimney diameter, it is

doubtful that the specific chimney cost decreases with an increase in chimney diameter. The initial cost of the chimney, Cc, can then be evaluated from:

Cc [€] = b хЯс X п x dc (2)

The cost of the collector is also evaluated using an approach introduced by Bernardes [4] who assumes an area specific collector cost of 9.85 €/m2. A cost model for each component of the PCU has been implemented. See the dissertation of Fluri for details [6].

To evaluate the cost of electricity a procedure described by Riggs et al. [8] is followed. The impact of insurance cost, tax incentives and carbon credits has been disregarded. An interest rate of 8%, an inflation rate of 3.5%, a depreciation period of 30 years and a construction period of 2 years have been assumed.

Using data of Schlaich [9], it can be shown that the operating and maintenance cost for the first year (in Euro) is linearly proportional to the collector area, Ac, (in m2) with the following trend:

OCi = 0.1364AC +604481 (3)

This approximation is used for the present study.

S. Gavrin 1, V. Simakin 2, S. Tyukhov 2, D. Strebkov3 I. Tyukhov2, 3

1 Nanocenter MPEI (TU), Energetichesky Proezd, 6, Moscow, 111 250 Russia

2 VEI, Krasnokazarmennaya, 12, Moscow, 111250, Russia

3 VIESH, 1st Veshnyakovski pr.2, Moscow, 109456, Russia

* Corresponding Author, itvukhov@yahoo. com

Abstract

This paper is devoted to the developing PV/T (photovoltaic /thermal) system based on the solar cells with vertical p-n-junctions and, more particularly, to nanodiagnostics of such solar cells. Paper describes tendencies in developing PV/T approaches, including concentrator PV/T systems and evolution of solar energy integrating technologies, concentrator PV/T system developed at the All-Russian Research Institute of Electrical Engineering (VEI) for research purposes, technology of the solar cells with vertical p-n — junctions. The images taken with the help of INTEGRA scanning probe microscope in Nanocenter of the Moscow Power Engineering Institute MPEI (TU) are shown.

Keywords: PV/T technology, solar cells with vertical p-n-junctions, nanodiagnostics

1. Introduction

The purpose of the paper is to describe the first results of a project which is carrying out at the All­Russian Research Institute of Electrical Engineering (VEI). The project is devoted to designing, building and testing of PV-thermal concentrator system based on solar cells with vertical p-n — junctions. Solar cells with vertical p-n-junctions have a number of advantages: high temperature tolerance, low series resistance, bifacial sensitive accepting surfaces suitable for bifacial illumination, low equilibrium temperature, quite simple technology of manufacturing etc. Low series resistance allows solar cells to work under high concentration ration.

J. Widen1*, E. Wackelgard1 and P. Lund2

1 Department of Engineering Sciences, Uppsala University, P. O. Box 534, 751 21 Uppsala, Sweden
2 Advanced Energy Systems, Helsinki University of Technology, P. O. Box 2200, FI-02015 HUT, Finland

Corresponding Author, ioakim. widen@angstrom. uu. se

Abstract

Extensive integration of distributed photovoltaic (PV) generation into residential areas is likely to be a challenge to the control of power quality in low-voltage distribution grids. Overproduction of power caused by mismatching load and demand profiles puts restrictions on the amount of distributed generation allowed locally in the grid at high penetration levels. This paper investigates the load matching capability of PV at Stockholm, Sweden, and how it can be improved by different measures; PV panel orientation, demand side management (DSM) and electricity storage. Detailed models for PV generation and household electricity load are used. Energy storage has the greatest potential of obtaining a better match between load and production in terms of solar fraction at system setups where the production is several times higher than the mean load, although both DSM and PV array orientation options have comparable impacts. At lower levels of overproduction, orientation and DSM options seem to be slightly more effective, mainly because of energy losses in the storage medium.

Keywords: Photovoltaics, Distributed generation, Load matching

1. Introduction

Utilization of solar energy is gaining increasing interest as a means of reaching sustainability in the built environment. In Sweden, and at high latitudes in general, direct generation of electricity with solar photovoltaics (PV) has traditionally been ascribed a low potential for contribution to the total domestic electricity demand. As recent studies have pointed out, however, grid-connected distributed PV, e. g. roof-top systems, could gain attention as an energy-saving measure in domestic buildings [1].

In Sweden, therefore, it seems likely that a more extensive integration of PV will start at the lowest voltage level of the distribution grid. This makes the load matching capability of the electricity production a critical issue. If production and load do not match, overproduction of power could lead to problems with power quality at high penetration levels of distributed generation, of which the main issue is voltage rise [2]. There are some theoretical studies on this effect for high latitudes (see for example [3], [4]) but almost no measurements or observations, because the critical amount of generation is yet to be integrated.

In this paper three options for improved load matching are studied. The first option is orientation of the photovoltaic arrays. For maximization of the array output at any instant of time, the incidence angle of the incoming radiation should be zero. For maximum annual production at high latitudes,
the optimal azimuth angle is due south, and the optimal tilt somewhat higher than the latitude. If matching with the evening or morning load is desirable, however, orientation eastward or westward could be an option, favouring morning and evening sun respectively.

The second option is altering the demand profile through demand side management (DSM). This refers to the active rescheduling of energy-demanding activities or appliances in the households. From a utility’s point of view, a smoothened load curve is desirable, which could be achieved by encouraging households to reschedule energy use to low-demand periods. For better load matching with photovoltaics, loads should instead be shifted toward mid-day.

These two options are compared to shifting of production to high-demand periods through energy storage. A description of the models used for generating electricity load and production data follows in Section 2. Section 3 describes the different load matching options in more detail and results of simulations for improved matching with household electricity load in detached houses are presented in Section 4.

2. Models

For the end-use-specific household electricity demand, a previously developed load model was used, validated and adjusted against preliminary measurements from the Swedish Energy Agency (SEA). For generation of photovoltaic electricity generation data, a detailed calculation procedure was applied to hourly series of direct and diffuse irradiation on the horizontal plane.

Air velocity under natural convection inside ducts varies across the duct as well as in the flow direction [7]. Consequently the unpredictable behaviour of airflow in ducts under natural convection requires high accuracy velocity measurements to successfully predict the airflow rate [8]. As the temperature of the top plate was increased, the warming of the air in contact with the plate surface created a buoyancy force, facilitating an upward flow in the duct. The generated heat at the surface was then absorbed by the air and carried along, reducing the surface temperature. The driving forces and the resistance to the air flow are identified and computed. Inherent to the flow inside the channel, are the pressure difference between the inlet and outlet air of the channel and the friction losses due to surface contact resistance.

2.2 Thermal conditions

The total inward heat flux (q ) is given by:

q’ = q" + qb (1)

qt represents the convective heat flux from the top front surface, and is defined by the temperature difference between the top plate front surface and the bulk mean air temperature at that point. The second path of carrying the energy into the air stream is represented by qb, which can be defined as the radiative

heat exchange between the top plate surface and the bottom plate (all radiation reaching the back surface is transmitted back into the fluid by convection). The primary heat flux from the bottom can then be expressed as:

qb = hr (Ttp — Tbp )

The radiation heat transfer coefficient (hr) can be expressed as:

hr = £ef a(TtP + Tbp )(Ttp + Tbp)

As a result of the asymmetric Ohmic heating (qn), the effective heat flux is given by:

(4) (5)
q = qQ qioss Assuming identical heat losses on the side insulations, the total heat loss was computed as:
Tbp Ta 1 ~T
T — T
■ + 2-
1
bins
h.
vbins

The convection heat transfer coefficient (hc) is a complex quantity as it depends on parameters such as the thermo physical properties of the fluid, flow type, as well as dimensional Nusselt number (Nu), which depends on Raleigh number (Ra) for natural convection case. The heat transfer coefficient was defined as:

°CT4 — Tb4p)
1
qt	(6)
11 — + —
T — T tp m
1

V S1 S2 J

Where sx and s2 are the emissivities of the upper and lower plates respectively. was computed as [9]:

where, the dry air density (pa) is given by:

P M P P

p =——— = = • — = 0.00348Kg. K / N. m—

RT R T T

The specific humidity (ш) was computed as the relative humidity was recorded by a Vaisala Humicap HMT 333 (Temperature Range: -40° to 80°C). The total energy (Q) carried by the inlet air in the channel is then expressed as:

The specific heat (C) was evaluated as [9]:

For dry air, Г = 1030.1-0.19762 • T + 0.0003947 • T 2(13)

pa ma ma

For humidified air we have:

Cp ф= Cpa • (1 + 1.792Ш)

3.2. Temperature Distribution

The air entering the channel is heated as it flows through the duct, and its temperature at any cross­section changes from temperature (T^) at the surface of the top plate to some minimum at the centre line

of the duct. The mean temperature T (at a distance x) will change in the flow direction as:

q x

a, x a, i

PmC pVm duct

Hence the mean air temperature at the exit of the channel is given by:

q Lduct

a, e a, i

PmVmC p duct