P. Bourdoukan1[16], E. Wurtz2, P. Joubert1 and M. Sperandio1

1 LEPTIAB, Universite de La Rochelle La Rochelle, Avenue Marillac, 17000 La Rochelle, France
2 Universite de Savoie, Campus Scientifique, 73376 Le Bourget du Lac, France
* Corresponding Author, paul. bourdoukan@univ-lr. fr

Abstract

Desiccant cooling powered by solar energy and using water as a refrigerant has a low environmental impact and appears as an important technique to reduce energy consumption in buildings. The cooling potential of the system is based on the performance of the desiccant wheel that removes humidity from outside air to increase the potential of the humidifier. In this paper a sensitivity analysis of the desiccant wheel dehumidification is performed using the design of experiments. The impact of outside temperature, outside humidity ratio, the regeneration temperature and the regeneration humidity ratio is studied on the dehumidification rate of the wheel using experimental and numerical results.

Keywords: solar desiccant cooling, sensitivity, experiments, simulation

1. Introduction

Solar desiccant cooling is a heat driven technique powered by solar collectors. It is based on evaporative cooling and utilizes a desiccant wheel to remove humidity from outside air. When adsorbing the humidity the desiccant needs to be regenerated by moderately hot air stream provided by solar collectors. This technology presents the advantages of being friendly environmental since its electrical consumption is limited to the auxiliaries (fans and pumps), beside it use water as a refrigerant in opposition to vapor compression technique using refrigerants with high environmental impact. The general scheme of a solar desiccant cooling plant is shown in the figure 1 below:

With reference to Fig. 1 the conventional cycle operates as follows: first, outside air (1) is dehumidified in a desiccant wheel (2); it is then cooled in the sensible regenerator (3) by the return cooled air before undergoing another cooling stage by an evaporative process (4), finally, it is
introduced into the building. The operating sequence for the return air (5) is as follows: it is first cooled to its saturation temperature by evaporative cooling (6) and then it cools the fresh air in the rotary heat exchanger (7). It is then heated in the regeneration heat exchanger (8) and finally regenerates the desiccant wheel (9) by removing the humidity before exiting the installation.

The task of the desiccant wheel is first to reduce the humidity of outside air in order to match indoor air standards and second to provide an extra dehumidification to increase the potential of supply humidifier. The desiccant wheel appears as a key component. The dehumidification performance of the desiccant wheel depends on the operating conditions [1] e. g. the wheel rotation speed, the air flow rate, the outside temperature and outside humidity, the regeneration temperature and regeneration humidity. Usually an optimum rotation speed and optimum air flow rate are recommended by the manufacturer thus these two parameters are constant during the operations but outside and regeneration conditions are not. So the performance of the desiccant wheel depends intrinsically on these parameters.

In this paper a sensitivity analysis is conducted on a desiccant wheel using the silica gel as an adsorbent to investigate the effect of outside and regeneration conditions on the performance of the desiccant wheel. The method used in this analysis is design of experiments (DOE) [2]

2. Sensitivity analysis

2.1. Design of experiments

In the DOE the response (y) of the studied phenomena influenced by different parameters or factors (xi) is expressed using a polynomial form [2]:

N N N •

the lower limit is the minimum required for the silica gel. For the regeneration humidity ratio range it is taken with the consideration of the outlet conditions of the return humidifier.

2.2. Experimental setup

The experimental installation of La Rochelle [1] is used for the measurements of the performance of the desiccant wheel. This experimental installation consists of a silica gel desiccant wheel and aluminum sensible regenerator and two rotating humidifiers. At the inlet and outlet of each component a psychrometer is used to measure the dry and wet bulb temperature. The local atmospheric pressure is measured too thus using the dry and wet blub temperature the humidity ratio is then measured accurately. At the desiccant wheel outlet, the dry bulb temperature and the humidity ratio are not uniform. In order to have an accurate measurement of the mean outlet temperature and humidity, three humidity measurements and 6 temperature measurements are performed simultaneously.

The major parts of the dehumidification rates (wi-w2) used in the sensitivity analyses are experimental measurements but when a combination of parameters is not possible experimentally numerical results of the desiccant wheel model are used to complete the required combinations.

The model used will be introduced in the following section.

The control system start the chiller only if a driving temperature above 72°C is available, and turns the machine off when it falls below 68°C (Fig. 5). The measured heat rejection temperatures were very favourable for the chiller: in 95% of the hours an inlet temperature to the machine between 18°C and 20°C was registered. These numbers show the effectiveness of the installed boreholes for the heat rejection in the present system. Chilled water temperatures (inlet temperature to the cooling coil) between 7°C and 14°C were measured. As a conclusion, the temperature lift defined as temperature difference between chilled water outlet and heat rejection temperature inlet to the machine was about 7.9K (Fig. 6).

The heat and mass transfer model for the desiccant wheel used below is based on the analogy method with heat transfer that occurs in the sensible heat regenerator. It was first introduced by Banks [3] and Maclaine cross [4] then Jurinak [5] and Stabat [6] improved the model. The following assumptions are considered:

• The state properties of the air streams are spatially uniform at the desiccant wheel inlet

• The interstices of the porous medium are straight and parallel

• No leakage or carry-over of streams

• The interstitial air velocity and pressure are constant

• Heat and mass transfer between air and porous desiccant matrix is considered using lumped transfer coefficients

• Diffusion and dispersion in the fluid flow direction are neglected

• No radial variation of the fluid or matrix states

• The sorption isotherm does not represent a hysteresis

• Air reaches equilibrium with the porous medium

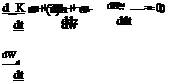The heat and mass conservation equations:

Heat and mass transfer equations:

Equations (2), (3), (4) and (5) are coupled hyperbolic non-linear. With the assumption of the Lewis number (Le), equal unity and the desiccant matrix in equilibrium with air means (Td= Teq and weq= wa). Banks [2] used matrix algebra and proved that these equations can be reduced using potential function Fi(T, w) to the following system:

(7)

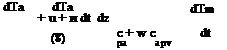Introducing the equations of heat transfer alone in the sensible regenerator as stated in [3]:

(12)

ncf is the efficiency of the counter flow heat exchanger for balanced flow.

F = h

(13)

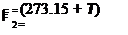
6360 (14)

The model described above, was implemented to SPARK [8] a general simulation environment based on equation. In the next section the model is validated experimentally.

From the 282 operation hours in the cooling mode about 35.8% (101 hours) no solar operation was possible. On 148 hours (52%) a complete solar operation covering the whole hour was possible, on the remaining 33 hours the solar system could only provide a part of the driving heat. From an energetic point of view, 59.8% of the driving energy over the whole cooling operation period came from the solar system.

The electricity consumption over the whole cooling period was 10% of the cooling energy. This electricity consumption includes the electricity needs for the chiller itself, the heat rejection via the boreholes, the driving circuit and the cold distribution to the cooling coil in the air handling unit. But it does not include the pump of the solar loop.

Fig. 5. Frequency diagram of driving temperatures Fig. 6. Frequency diagram of temperature lifts.

(from heating net or solar system).

Calculating an electric COP for the whole system as the cooling energy produced per kWh of electric energy consumed, an electric COP of approximately 10 can be derived. It has to be noted however, that although energy efficient pumps have been used, all pumps operate at constant volume flows independently of the chillers output power. Thus a constant electricity consumption of about 500W is measured during operation. Optimising the control, e. g. using a flow rate control when low cooling capacity is needed may give potential for reducing the electricity consumption.

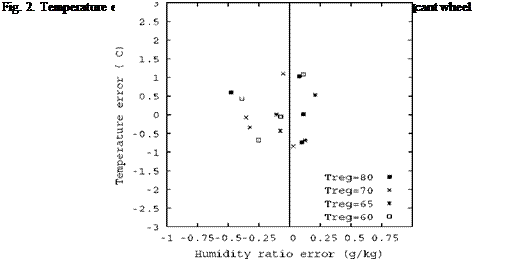The experimental installation presented in section 2 is used to validate the above presented model. Different inlet conditions were considered with temperature varying form 25°C to 38°C and humidity ratio from 10 to 15 g/kg and for different regeneration temperature (55°C, 60°C 65°C, 70°C and 80°C).

The figure 2 [9] plots the temperature error versus the humidity ratio error for the most significant points. It shows the maximum predicted error 0.4 g/kg and root mean squared error (RMSE) is 0.22 g/kg. For the temperature and the maximum committed error in the outlet temperature is 1 °C for RMSE of 0.65 °C. It must be noted that the uncertainty in the measurement of the mean values is 0.7°C for the temperature and 0.3 g/kg. It shows that the committed errors are in the domain of the uncertainty of the measurements.

In the following section the experiments are performed on the desiccant using experimental measurements and numerical results in order to perform the sensitivity analsysis.

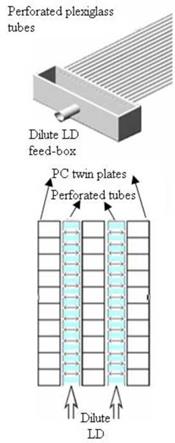
In this heat and mass transfer prototype, the desiccant solution and the air stream is brought into contact with each other in a cross flow configuration. The regenerator consists of a stack of polycarbonate (PC) twin wall plates. Each plate has an internal heating water circuit. The plates are covered with a wick fibre to facilitate intimate contact between the liquid desiccant and air. This is done to increase the exposure time over the plates and thereby enhance the desired mass transfer and heat exchange. The general design is shown in the left part of Fig. 2.

The advancement of the distribution system consists of:

• a separation between the liquid desiccant distributor and the contact area between air and desiccant. The LiCl solution is distributed over the textile separately in an advance stage i. e. before coming in contact with the air stream. A separator is used to split the generator into two chambers. In the upper small chamber LiCl throttled through perforated plexiglass tubes, completely diffused through the textile fibres and trickles down to come in contact with the horizontal air stream in the lower large chamber. This separator will prevent LiCl particles to drift into the air stream, resulting in a zero carryover regenerator.

• the employment of promising fibres, a new natural man made fibre produced from wood pulp. This fiber can absorb 50% more moisture than cotton did, it has a lower sorption index than cotton, which means higher transport speed of the liquid.

• the employment of perforated plastic tubes with different tested throttling-points diameters.

The LD distributor in this design uses a plurality of parallel plexiglass tubes to horizontally distribute the LD over the wick. The parallel tubes extend outwardly from openings in the lower edge of one of the sides of a LD feed box and are closed from the free end. The tubes penetrate the PC plates horizontally and deliver the desiccant solution over the coated plates at a number of equally spaced-apart locations (discharge-holes). The distributor is shown on the right part of Fig.

2.

The discharge holes are preferably formed on the plexiglass tubes by using a CNC machine to make the fine drip points with high precision. The size and number of the discharge holes are selected to provide the desired liquid flow. The throttling-point density determines the flow into the wick material covering the PC twin-wall plates. Likewise, the distance between the discharge — holes is selected to accommodate the desired LD flow rate with the maximum even distribution.

The regenerator consists of an upper and a lower hot water-feeder box. Each water feeder box consists of four equal chambers separated by baffles. Hot water will pass through the internal passages of the PC twin-wall plate in a 3-loop serpentine path. It will enter the first chamber from a primary opening in the upper wall of the chamber, and it collides with a liquid spreading surface that faces the internal PC passages. The spreading surface will also disrupt the downward flow of water and will direct it equally to the channels.

Fig. 2. Exploded view of generator design along with the illustration of flow directions of heating water, LD and air (upper left), an isometric enlargement of the LD distribution system and a top-view of how the glass tubes penetrate the polycarbonate twin-plates (upper right).

In Erro! A origem da referenda nao foi encontrada. an example of the operation during a normal summer day is shown. The diagram corresponds to June 13th, 2007. Cooling operation starts at 7:30 and ends at 14:30. In the morning till 11:30 the chiller is operated with heat from the heating net as the temperature in the solar storage was not sufficient to operate the machine. The shaded area between 11:30 and 14:30 shows the time when the system was operated with heat from the solar system.

Large temperature variations can be observed in the driving circuit. While the cyclic temperature peaks observed in the return flow from the chiller in all circuits (T_HT_out, T_MT_out and T_NT_out) are characteristic of the periodic working adsorption machine, the variations in the driving inlet temperature (T_HT_in) are due to the dynamic behaviour of the plate heat exchanger within this circuit but also variations in the temperature of the heating net. These variations were not expected. A much more stable inlet temperature is observed during the solar operation period. Further it can be seen, that the boreholes effectively attenuate the temperature peaks giving smooth and constant feed temperatures (T_MT_in) to the machine.

4.1. Heating operation

For the heating operation the adsorption chiller is operated as a heat pump. For this operation the evaporator is connected to the borehole system and the heat rejection to the heating coil in the air handling unit.

4.1 Results

Experiments have been conducted on the desiccant wheel with the parameters (e. g. outside temperature, outside humidity ratio, regeneration temperature and regeneration humidity ratio) varying in the range defined in the section 2. The complete DOE of 4 parameters operating between 2 levels needs 24=16 experiments. When a combination of the studied parameters was

difficult to achieve experimentally (3 experiments) the results of the model was used to complete the DOE. Table 1 below shows the results

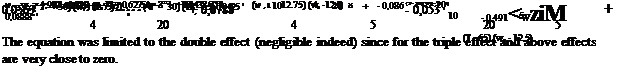
Solving 16 equations for the effects identified in the equation (1). The dehumidification of the desiccant wheel is then written in function of the operating parameters

4.2 Analysis

Form the equation identified we notice a constant dehumidifying effect of 4,987 g/kg which will be increased or decreased depending on the operating conditions. In order to compare the effect of each parameter with the constant effect, they are divided by this later and a graphical comparison can thus be established. The figure below shows the effect of each parameter.

As commonly known, figure 3 shows tha the regeneration temperature has the most significant impact on the dehumidification performance of the desiccant wheel. In the same time outside conditions has an important impact on too.

• Increasing the regeneration temperature from the mean value (65°C) to its upper limit will increase the dehumidification 23%

• Increasing the outside temperature to its higher limit will decrease the dehumidification of 17%.

• Increasing the outside humidity ratio will increase the performance of the desiccant wheel of 13%

• Increasing the regeneration humidity ratio will decrease the performance of the desiccant wheel of 8%.

The reason behind these observations is the vapor pressure difference of the air and that of the surface of the silica gel. This vapor pressure difference is the driving force of the adsorption phenomena. Reminding that if the desiccant is cold the vapor pressure at its surface. For the moist air the temperature does not have a significant impact on the vapor pressure while humidity ratio does.

The desiccant coming for the regeneration sector is hot and dry, it is first cooled down by the outside air in the process sector and then the adsorption occurs.

So if we increase the temperature of the outside air its vapor pressure will not increase significantly in reversal it will not cool sufficiently the hot desiccant form arriving from the regeneration sector yielding a high vapor pressure at the surface of the desiccant and thus the adsorption will be less efficient. If we increase the humidity ratio of the outside air its vapor pressure will increase significantly yielding a higher vapor pressure difference thus increasing the adsorption. When increasing the regeneration temperature, the regeneration air vapor pressure does not increase significantly while the desiccant is heated and its vapor pressure increases leading to an efficient drying of the desiccant. This desiccant leaving the regeneration sector is dry and thus having fewer vapor particles, yielding a low vapor pressure at its surface and thus high adsorption. When increasing the regeneration humidity ratio we will increase the vapor pressure of regeneration air stream, reducing the transfer from the desiccant to the regeneration air, yielding less drying of the desiccant. When the sorbent will leave the regeneration with more water vapor at its surface its vapor pressure is then higher, reducing thus the adsorption.

This clearly shows the limitations of the desiccant cooling technique regarding outside conditions. It demonstrates that high outside temperature reduces significantly the performance of the desiccant wheel. Regarding the outside humidity ratio even if the dehumidification increase with increasing outside humidity ratio, we noticed that for outside temperature beyond 30°C the maximum dehumidification rate is 6 g/kg. Taking into account the maximum humidity inside the building (e. g. 11.8 g/kg) and the humidification across the supply humidifier we conclude that the maximum outside humidity under which a desiccant system will operate efficiently is 14.5 g/kg.

3. Conclusion

In this paper a sensitivity analysis based on the design of experiments was conducted on a desiccant wheel using mainly experimental results. A numerical model was validated experimentally and provided the missing combination of the experiments. The impact of the outside and regeneration conditions on the dehumidification rate of the desiccant wheel was studied. As widely known the regeneration temperature has the most significant impact on the dehumidification rate, but the impact of the outside temperature, outside humidity ratio and the

regeneration humidity ratio are very important as well. These results showed that desiccant cooling is an interesting option for moderately hot and moderately humid climates

Nomenclature

Acknowledgments

The authors would like to thank Mr Michel Burlot for his valuable technical support on the experimental

installation. This work was supported by ADEME (French Agency of the Environment and Energy

Management) and the regional council of Poitou Charentes.

References

[1] P. Bourdoukan., E. Wurtz., P. Joubert., M. Sperandio,. (2008). Potential of solar heat pipe vacuum collectors in the desiccant cooling process: modelling and experimental results. Solar Energy. 0.1016/j. solener.2008.06.003

[2] J. Goupy, (2001). Introduction aux plans d’experiences, Dunod.

[3] P. J. Banks, (1972). Coupled equilibrium heat and single adsorbate transfer in field flow through a porous medium — 1. Caracteristics potentials and specific capacity ratios. Chemical Engineering Science, 27, 1143-1155.

[4] I. L. Maclaine-cross, P. J. Banks, (1972). Coupled heat and mass transfer in regenerators — prediction using analogy with heat transfer. Int. J. Heat Mass Transfer, 15, 1225-1242.

[5] J. J. Jurinak. (1982). Open cycle solid dessicant cooling — component models and system simulation, Ph. D, Winconsin, Madison.

[6] P. Stabat, (2003). Modelisation de composants de systemes de climatisation mettant en oeuvre l’adsorption et l’evaporation d’eau, Ph. D, Ecole des Mines, Paris.

[7] W. M. Kays, A. L London, (1984). Compact Heat Exchangers, McGraw-Hill, New York.

[8] SPARK. (2003). Simulation Problem Analysis and Research Kernel. LBNL, Berkeley, California.

[9] P. Bourdoukan., E. Wurtz., P. Joubert., M. Sperandio, (2008). Critical efficiencies of components in desiccant cooling cycles and a comparison between the conventional mode and the recirculation mode."

In proceedings of ECOS conference, Krakow, Poland, 1, 435-443

Two different sets of experiments were carried out to prove the advancements on the distribution system.

1. The objective of the first test is to determine the optimal size and number of discharge points distributed along the plastic tube. The optimized tube will serve the LD flow rate required by the application and ensure fairly equal amounts of the LD throttled-out through each discharge bore. Five perforated plastic tubes are tested. Each tube is perforated by a CNC machine in equally-spaced positions. H2O/LiCl (30% salt concentration by weight) is used as the liquid desiccant with three volume flow rate values. In order to investigate the effect of the distance between the LiCl feed-box and the discharge-point location, different positions along the tube are selected. Transparent PVC hoses are used to enclose the discharge-bores, without affecting the throttled LiCl. The free ends of the PVC hoses are connected to plastic bottles in order to collect the LiCl throttled out of the intended discharge-bore. Fig. 3 shows the experimental setup.

2. The second test is a comparison between different types of textiles (100% cotton, 100% viscose, 100% polyester, 100% polyamide and wood pulp based textiles) with different thicknesses and different weaving. Each type of the mentioned textiles has been tested to measure the absorption capacity and the diffusion speed by simply pouring a quantity of LiCl onto the upper surface of a taut piece of textile, and measuring the needed time for the LiCl droplets to be completely absorbed by the textile fibers. Each type has been tested in both, dry and wet state. Then PC plates were coated with the textiles which show the best absorption and diffusion speed, and exposed to a LiCl solution throttled through the perforated plexiglass tube. A violet fluorescent light and dyes have been used to support the visual inspection of LiCl distribution through the textile fibers. Fig. 3.

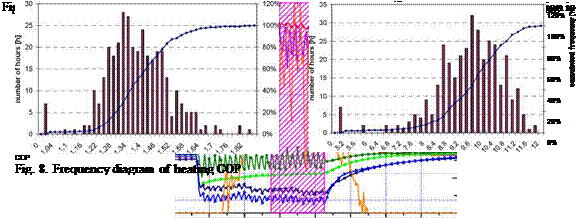
As for the cooling operation, for the following statistics on hourly values, only hours with a constant operation of the machine were considered in order to be sure to consider steady state conditions only. This covers more than 63% of the hours with operation, as can be deduced from Table 1. Fig. 8 shows the frequency diagrams of the hourly COP and heating powers (Fig. 9). For the whole heating operation period a thermal COP of 1.43 is obtained. The hourly mean heating power was 9.43kW with a standard deviation of 1.59kW.

in the period between 11:30 and 14:30.