The heat and mass transfer model for the desiccant wheel used below is based on the analogy method with heat transfer that occurs in the sensible heat regenerator. It was first introduced by Banks [3] and Maclaine cross [4] then Jurinak [5] and Stabat [6] improved the model. The following assumptions are considered:

• The state properties of the air streams are spatially uniform at the desiccant wheel inlet

• The interstices of the porous medium are straight and parallel

• No leakage or carry-over of streams

• The interstitial air velocity and pressure are constant

• Heat and mass transfer between air and porous desiccant matrix is considered using lumped transfer coefficients

• Diffusion and dispersion in the fluid flow direction are neglected

• No radial variation of the fluid or matrix states

• The sorption isotherm does not represent a hysteresis

• Air reaches equilibrium with the porous medium

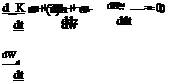The heat and mass conservation equations:

Heat and mass transfer equations:

Equations (2), (3), (4) and (5) are coupled hyperbolic non-linear. With the assumption of the Lewis number (Le), equal unity and the desiccant matrix in equilibrium with air means (Td= Teq and weq= wa). Banks [2] used matrix algebra and proved that these equations can be reduced using potential function Fi(T, w) to the following system:

(7)

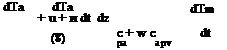Introducing the equations of heat transfer alone in the sensible regenerator as stated in [3]:

(12)

ncf is the efficiency of the counter flow heat exchanger for balanced flow.

F = h

(13)

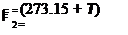
6360 (14)

The model described above, was implemented to SPARK [8] a general simulation environment based on equation. In the next section the model is validated experimentally.