The parallel lines in 3D space appear in the image to meet at a point when their plane is not parallel to the image plane (Figure 4). This point of convergence is called the vanishing point and can be used to determine distances in the real world [2]. The vanishing point of lines is sufficient to analyze and detect the edges without the need for completely calibrating the camera used. In the case of the BiFres system, the structure frame of the concentrator is a rectangle with four metal sides. The four corners are easy features to locate from the pictures and their coordinates are used to form the equations of lines. The equations of lines are solved simultaneously to locate their intersection; the vanishing point. With the knowledge of the actual dimensions of the concentrator and their corresponding image pixel counts, a scaling factor is obtained which converts the image pixels to space dimensions. Using triangle similarities, the coordinates of any image point on the reference lines are then directly related to the actual distance Xm. This information is further fed into the geometrical algorithm for the calculation of the real surface slope at the specified point on the mirror. It is important to mention that the above method is an approximation because the mirrors do not lie in the same plane of the concentrator frame; each mirror has a different tilt angle.

However, the effect of this tilt is less apparent because the camera is located at a large distance from the concentrator between 18 to 30 meters away.

6. Results and analysis

The following graphs show the error map of the surface of each mirror as well as the root mean square error for the whole mirror with the concentrator at vertical and inclined positions. Presented here are only the 15 mirrors of the left part of the concentrator.

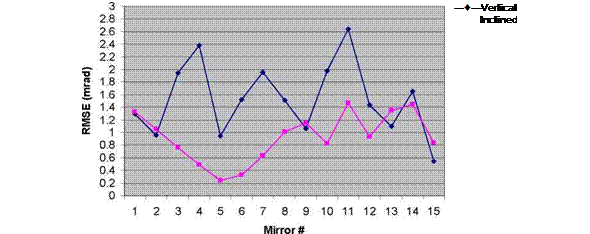The two graphs show that the mirrors at the inclined position posses surface errors within the range of 3 mrad compared to the vertical position that shows errors up to 4.5 mrad. In the vertical position, RMS errors are between 0.54 and 2.63 mrad while in the inclined position they are between 0.23 and 1.46 mrad. These values are within the range of RMSE and comply with surface errors quoted for other concentrator systems [1, 4, 10]. The results contradict the expectations that at inclined positions the RMSE should be higher than that at the vertical position due to the mirrors bending under their own weight. The reason for this is that during tracking, the motor exerts a lot of power to retain the concentrator to its horizontal position. The motor moves slower than usual and this affects the tracking precision. Therefore a heavy counter balance is attached to the concentrator frame to help the motor during its movement. The balance is made of heavy iron bars connected to centre body of the concentrator and balanced with cable wires to the corners of the structure. In the vertical position, the bars are perpendicular to the frame and parallel to the ground. At this position the cable wires are at their highest tension and exert stresses on the structure and consequently the mirrors holders. On the other hand, when the concentrator is at an angle, the bars exert less torque on the structure and the overall effect on the mirrors is less pronounced.

7. Conclusion

The absorber reflection method has been used to assess the surface slope errors of a linear Fresnel PV/T concentrator. The absorber reflection method has proved to be an effective and simple tool to obtain slope error map of reflecting concentrating systems. Results show that mechanical stresses on the structure, where mirrors are attached, play an important role in the errors. Structure manufacturing should be precise because mirror misalignments can cause the reflected rays to be blocked by the preceding mirror thus increasing the non-uniform illumination and shading effects on the modules. The counter balance should be redesigned to avoid its negative implications. The experiment has shown that the accuracy in locating the camera is a crucial point for the reliability and accuracy of the measurements.

8. Acknowledgments

This work has been supported by the 6th European Union Research Programme’s Marie-Curie early

stage research training network “Advanced solar heating and cooling for buildings — SOLNET”.

References

[1] J. Coventry (2004), A solar concentrating photovoltaic / thermal collector. PhD thesis. Australian National University

[2] H. Doehler, B. Korn, Robust position estimation using images from an uncalibrated camera. Digital

Avionics Systems Conference, 2003. DASC ’03. The 22nd Volume 2, 12-16 Oct. 2003. Pages:9.D.2-9.1-7

[3] E. T Franklin, J. S. Coventry, Effects of highly non-uniform illumination distribution on electrical performance of solar cells. Proceedings of Solar 2002 — Australian and New Zealand Solar Energy Society

[4] S. A. Jones, J. K. Gruetzner, R. M. Houser, R. M. Edgar, T. J. Wendelin, VSHOT: a tool for characterizing large, imprecise reflectors. Annual international symposium on optical science, engineering, and instrum­entation, Denver, Colorado USA, November 1996. Department of Energy

[5] S. Kammel, F. P. Leon, Deflectometric measurement of specular surfaces. Instrumentation and Measurement (2008), IEEE Transactions 57, pp. 763-769.

[6] M. C. Knauer, J. Kaminski, G. Hausler, Phase measuring deflectometry: a new approach to measure specular free-form surfaces. Optical Metrology in Production Engineering. Proceedings of the SPIE (2004), volume 5457, pp. 366-376

[7] K. Pottler, E. Lupfert, G. Johnston, M. Shortis, Photogrammetry: A powerful tool for geometric analysis of solar concentrators and their components. Journal of Solar Energy Engineering (2005). 127, pp. 94-101.

[8] M. R. Shortis, G. Johnston, Photogrammetry: An available surface characterization tool for solar concentrators, Part II Assessment of surfaces. Journal of Solar Energy Engineering (1997). 119, pp. 286­291

[9] M. R. Shortis, G. Johnston, Photogrammetry: an available surface characterisation tool for solar concentrators — Part I: measurement of surfaces. Journal of Solar Engineering (1995). 118 (3), pp. 146-150.

[10] S. Ulmer, B. Heinz, K. Pottler, E. Lupfert, Slope error measurements of parabolic troughs using the reflected image of the absorber tube. 13th International Symposium on concentrating solar power and chemical energy technology: SolarPaces. Seville, Spain. June 20-23, 2006.

[11] T. Wendelin, K. May, R. Gee, Video scanning Hartmann optical testing of state-of-the-art parabolic trough concentrator. Solar 2006 Conference (ISEC’06).July 8-13, 2006.Denver, Colorado USA

[12] T. Wendelin, Parabolic trough optical characterization at the National Renewable Energy Laboratory. 2004 DOE Solar Energy Technologies Program Review Meeting October 25-28, 2004 Denver,

Colorado

[13] T. Wendelin, G. J. Jorgensen, R. L. Wood, SHOT: A method for characterizing the surface figure and optical performance of point focus solar concentrators. In: Solar Engineering. American Society of Mechanical Engineers, New York, (1991) pp. 555-560.