Air velocity under natural convection inside ducts varies across the duct as well as in the flow direction [7]. Consequently the unpredictable behaviour of airflow in ducts under natural convection requires high accuracy velocity measurements to successfully predict the airflow rate [8]. As the temperature of the top plate was increased, the warming of the air in contact with the plate surface created a buoyancy force, facilitating an upward flow in the duct. The generated heat at the surface was then absorbed by the air and carried along, reducing the surface temperature. The driving forces and the resistance to the air flow are identified and computed. Inherent to the flow inside the channel, are the pressure difference between the inlet and outlet air of the channel and the friction losses due to surface contact resistance.

2.2 Thermal conditions

The total inward heat flux (q ) is given by:

q’ = q" + qb (1)

qt represents the convective heat flux from the top front surface, and is defined by the temperature difference between the top plate front surface and the bulk mean air temperature at that point. The second path of carrying the energy into the air stream is represented by qb, which can be defined as the radiative

heat exchange between the top plate surface and the bottom plate (all radiation reaching the back surface is transmitted back into the fluid by convection). The primary heat flux from the bottom can then be expressed as:

qb = hr (Ttp — Tbp )

The radiation heat transfer coefficient (hr) can be expressed as:

hr = £ef a(TtP + Tbp )(Ttp + Tbp)

As a result of the asymmetric Ohmic heating (qn), the effective heat flux is given by:

(4) (5)
q = qQ qioss Assuming identical heat losses on the side insulations, the total heat loss was computed as:
Tbp Ta 1 ~T
T — T
■ + 2-
1
bins
h.
vbins

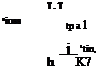The convection heat transfer coefficient (hc) is a complex quantity as it depends on parameters such as the thermo physical properties of the fluid, flow type, as well as dimensional Nusselt number (Nu), which depends on Raleigh number (Ra) for natural convection case. The heat transfer coefficient was defined as:

°CT4 — Tb4p)
1
qt	(6)
11 — + —
T — T tp m
1

V S1 S2 J

Where sx and s2 are the emissivities of the upper and lower plates respectively. was computed as [9]:

1 + Ф 1 +1.608^

(7),

Pa

P

where, the dry air density (pa) is given by:

P M P P

p =——— = = • — = 0.00348Kg. K / N. m—

RT R T T

The specific humidity (ш) was computed as the relative humidity was recorded by a Vaisala Humicap HMT 333 (Temperature Range: -40° to 80°C). The total energy (Q) carried by the inlet air in the channel is then expressed as:

Q = qb Aduct	mCp (Tae — Tap )
(9)

The specific heat (C) was evaluated as [9]:

For dry air, Г = 1030.1-0.19762 • T + 0.0003947 • T 2(13)

pa ma ma

For humidified air we have:

Cp ф= Cpa • (1 + 1.792Ш)

3.2. Temperature Distribution

The air entering the channel is heated as it flows through the duct, and its temperature at any cross­section changes from temperature (T^) at the surface of the top plate to some minimum at the centre line

of the duct. The mean temperature T (at a distance x) will change in the flow direction as:

q x

a, x a, i

PmC pVm duct

Hence the mean air temperature at the exit of the channel is given by:

q Lduct

a, e a, i

PmVmC p duct