Одним из недостатков ЛЛФ, особенно стеклянных, изготов­ленных методом прокатки расплавленного стекла, является то, что невозможно их сделать короткофокусными из-за наличия больших внутренних напряжений в стекле и влияния кованности. Поэтому мо­дули с ЛЛФ с фокусным расстоянием 500 мм получаются громоздки­ми и тяжёлыми. Исправить это положение позволяет фокусируемый коллектор солнечной энергии [3.4], представленный на рис. 3.9.

Принцип построения такого коллектора состоит в следующем: линза 3 фокусирует падающее солнечное излучение в фокус Fi, на пути лучей находится гиперболический отражатель 1, один фокус которого совмещён с фокусом F], а другой находится внутри про­странства линза-отражатель. Положение F2 может совпадать с цен­тром тяжести модуля. Отражающая поверхность отражателя 2 нахо­дится внутри модуля и защищена от прямых атмосферных воздейст­вий. Глубина модуля Н при этом не превышает 100 мм, что умень­шает эти величины не менее чем в 5 раз. После изготовления модуля были проведены его испытания на эффективность угловых дефоку­сировок и на определение концентрации.

Модуль был выполнен следующим образом: ЛЛФ имела ги­перболический цилиндрический отражатель, в фокусе которого ус­тановлен приёмник излучения в виде трубы диаметром 20 мм с за­щитной стеклянной трубой диаметром 30 мм. Таким образом улуч­шалась теплоизоляция приёмника от конвективных потерь во внут­реннем пространстве.

Эксперимент проводился калориметрированием модуля с по­мощью замера теплоты протекающей воды. Суммарный КПД нагре­вателя составил 44% в прицельном положении. Невысокие значения эффективности объясняются низкой оптической эффективностью ЛЛФ (50%) и коэффициентом отражения плёнки отражателя (75%), при этом концентрация излучения возросла с 5Х до 7Х.

Рис. 3.9. Схема работы
фокусирующего коллекто-
ра: ЛЛФ 3 фокусирует из-
лучение в фокус Fi, гипер-
болический отражатель 1
направляет излучение
в фокус F2, при этом умень-
шаются габаритные разме-
ры коллектора и увеличи-
вается концентрация на
приёмнике

Показано, что модуль может использоваться при одноосном слежении с падением эффективности на 10% при сезонных отклоне­ниях солнечного излучения на 25° (рис. 3.10).

Результаты экспериментальной проверки данного модуля: площадь ЛЛФ 0,35×2,0 м =0,7 м2, мощность прямой радиации 862 Вт/м2, температура воздуха +23,5°С, расход воды 5,37 л/чм2, темпе­ратура воды на входе +37,5 °С, удельная мощность 378 Вт/м2. Мо­дуль может рассматриваться как перспективный для получения вы­соких температур теплоносителя (до 140°), что представляет интерес для солнечных кондиционеров и холодильников.

На рис. 3.1 изображена ЛЛФ, выполненная из стекла, методом проката стекла без дополнительной механической обработки рабо­чей поверхности. Поверхность рабочих граней имеет явно выражен­ную неровность в виде «кованного» стекла, что приводит к доста­точно сильной диффузной составляющей прошедшего излучения и увеличению фокальной полосы. Суммарное светопропускание таких линз в пределах 50 — 60 %.

На рис. 3.6 показано изменение мощности на фокальной поло­се при поперечной и продольной угловых дефокусировках для фото­электрического модуля.

Схема эксперимента по исследованию угловых дефокусиро­вок демонстрируется на рис. 3.7. Модуль с небольшой по длине линзой (0,5 м) был установлен на поворотном стенде экваториаль­ной схемы слежения (ось вращения направлена на полюс Мира), на котором имитировались угловые отклонения. Продольные угловые отклонения обозначались а, поперечные, имитирующие отклоне­ния по склонению, обозначены углом у. Эксперимент прово­дился следующим образом: первоначально модуль устанавливался

Прицельное

положение

в «прицельное положение» на Солнце, снимались с помощью скани­рующего датчика распределения освещённости в фокальной плоско­сти, затем задавались поперечные отклонения Ду = 15°, 30°, 35°, при каждом значении Ду путём поворота вокруг оси вращения снима­лись показания для продольной дефокусировки а = 10°, 20°, 30°.

Измерения освещенности в фокусе проводились фотоэлектри­ческим датчиком размером 1 х 1 см, шаг измерения 1 см, определя­лась концентрация в направлении AF’. Графики концентрации пред­ставлены на рис. 3.8.

При продольных отклонениях а = 10°, 20°, 30° уход вдоль фо­кальной линии AF составил соответственно: 90,180,290 мм.

Для углов Лу = 15°, 30°, 35° уход в сторону от главной фокаль­ной линии AF’ составил соответственно 134, 290, 350 мм.

Максимальная концентрация излучения 4,5 — 5Х.

Общий вид линейной линзы Френеля (ЛЛФ) показан на рис. 3.1.

Расчёт профиля линз Френеля (круговых и линейных) приве­ден в главе 2. Рассмотрим работу ЛЛФ в режимах угловых дефоку­сировок, главным образом продольных отклонений вдоль направле­ния рабочего профиля [3.1].

В силу ряда особенностей ЛЛФ вызывают интерес у исследо­вателей и проектировщиков модульных солнечных электростанций (СЭС) с фотоэлектрическими преобразователями энергии. При од­ноосевом слежении за Солнцем таких модулей характерны так на­зываемые продольные угловые дефокусировки, определяемые углом между направлением прямых солнечных лучей и нормалью к несу­щей плоскости линз, расположенным в плоскости осевой симметрии ЛЛФ. В большинстве случаев этот угол переменен в течение дня и сезонов года, а также зависит от монтировки модуля на местности, которая обусловлена его ориентацией относительно сторон света и плоскости горизонта. Естественно, на величину угла продольной дефокусировки линейной ЛЛФ влияет также географическая широта местности.

Здесь имеется определенная аналогия со случаями использо­вания в составе модулей СЭС параболоцилиндрических зеркальных концентраторов, поле концентрации в которых формируется по за­конам зеркального отражения. Однако в основе формирования поля концентрированного излучения в ЛЛФ лежит механизм преломле­ния излучения на призмах, который и определяет специфику рас­сматриваемых ниже оптических и, как следствие, энергетических эффектов.

На рис.3.2 приведена схема хода лучей в продольных (а) и поперечных (Р) дефокусировках. При этом приняты следующие до­пущения: рабочие грани ЛЛФ представляют призмы с плоскими гранями, апертурный угол в «прицельном» положении Uo, главная фокальная плоскость линзы F0 содержит расчётную фокальную ли­нию F(0) с расстоянием f0, показатель преломления материала п, дисперсионные (хроматические) эффекты в данном случае не учи­тываются.

На рис. 3.2 показан ход лучей, преломленных периферийной призмой с апертурным углом отсчитанным в поперечном (глав­ном) сечении линзы. Главная фокальная плоскость линзы F0 содер­жит расчетную фокальную линию F(0), общую для всех призм лин­зы, и характеризуется главным же фокусным расстоянием линзы f0 в зависимости от принятого расчетного показателя преломления мате­риала п. В режиме продольной угловой дефокусировки на угол а. может быть намечена условная фокальная плоскость Fa(u0), которая смещена относительно главной на расстояние Afa(Uo).

Анализ работы косых лучей в призме проведён по методике А. И. Тударовского [3.2].

При традиционном прямом преломлении луча в призме, когда угол а=0, падающий и преломленный лучи лежат в главной плоско­сти призмы, при этом ширина фокальной полосы в расчетном случае при монохроматическом приближении формируется периферийной призмой и, как было показано в главе 2, поперечный размер фокаль­ного пятна определяется как:

dm=2f0(cp0Z)/cosu0, (3.1)

где элементарный солнечный луч имеет угловой полуразмер <р0 =16 угл. мин =4,65-10-3 рад, а мера прироста выходного угла фотометри­ческого пучка после преломления для призмы с и0 = 20° учитывается коэффициентом Z ~ 1,5 (см. раздел 2.4).

Для такой призмы характерный угол а0 при вершине

tga0 = sinUo/(n — cos u0), (3.2)

что при показателе преломления материала призмы п = 1,5 состав­ляет приблизительно a0=31,4°.

В режиме продольной угловой дефокусировки в призмах ЛЛФ мы имеем дело с косым преломлением. Это означает, что по отно­шению к главной плоскости призмы (нормальной к ребрам и гра­ням) дважды преломленные в призме лучи расположены в некото­рых косых плоскостях, положение которых по отношению к главной плоскости линзы зависит от значительного числа факторов.

В [3.2] при рассмотрении косого прохождения луча через призму (рис. 3.3) вводится специальная система отсчета направле­ния ребра призмы Pi Р2, нормалей п, и п2. Здесь углы ц, ц, i2, i2 суть характерные углы падения и преломления луча, направления которого отмечены векторами А’,Ап, Ам.

Для показанного на рис. 3.2 случая нормаль п, , падающий

луч А’ и вектор ребра р лежат в горизонтальной плоскости, когда входная грань призмы вертикальна. Соответственно в горизонталь­ной плоскости находятся углы а = — ц и вспомогательный вх, а так­же угол преломления Іі’.

Поперечная каустика при продольной дефокусировке. Далее выполняем конкретный расчет применительно к ЛЛФ с угловой апертурой 110=20° (на сторону) для периферийной призмы, показан­ной в масштабе своим условным главным сечением на рис. 3.4.

При отсутствии угловой дефокусировки (а=0) расчетный ход дважды преломленных лучей на рис.3.4 выделен пунктиром, приво­дящим преломленный луч А^ в расчетную фокальную линию лин­зы F(0). Очевидно, что фокальное расстояние f0R/tgu0= R/tg50, по­скольку для периферийной призмы и0 = 80 (R — расчетная полуши­рина ЛЛФ).

Согласно методике А. И. Тудоровского [3.2], ход косых лучей, падающих на входные грани условных призм, представляется про­екциями преломленных лучей на главную плоскость призм посред­ством введения взамен действительных углов 5а. их проекций 8а .

Режим продольной угловой дефокусировки представлен на рис. 3.4 ходом проекций на главную плоскость лучей дважды косо преломленных условной призмой с ио=20° при углах входа а 15, 30,45 и 60°. Помимо уже введенных обозначений лучей А’, А" Аи углов, здесь использованы следующие обозначения:

— углы 5а , являющиеся проекциями углов 5а;

— проекции отрезков fa,«отсекаемых» на следе оптической плоскости линзы проекциями преломленных лучей;

— отрезки Af„ , на которые уменьшается расчетное фокальное

расстояние ЛЛФ за счет продольной угловой дефокусировки;

— расчетная ширина полосы в фокальной плоскости, облучае­мой В режиме продольной угловой дефокусировки, da.

Угол отклонения луча 8 призмой всегда меньше угла д , со­ответствующего отклонению проекции луча на плоскость главного сечения. Естественно, что при этом fa < f0.

Приведенный на рис. 3.4 ход проекций косых преломленных лучей отображает лишь одну из особенностей работы линейных ЛЛФ в режиме продольной угловой дефокусировки, поскольку от­носится к одной периферийной призме линзы.

Режим совокупности призм в составе линзы более полно харак­теризует построение, выполненное на рис. 3.5 для ЛЛФ, состоящей из четырех условных призм, для углов a 30 и 60°. Показано, что каждая из призм формирует дважды преломленные лучи, проекции которых на главную плоскость образуют каустику, положение и размер которой в поперечном направлении зависят в первую очередь от угла а.

По дискретным преломлённым лучам на рис. 3.5 поверхность каустики дана как огибающая.

Очевидно, что указанное явление снижает эффективность ра­боты ЛЛФ как гелиотехнического концентратора. Иначе говоря, концентрирующая способность ЛЛФ в режимах продольной дефо­кусировки оказывается заметно сниженной по сравнению со случая­ми «прицельного положения», когда a = 0, а зона повышенной кон­центрации в таком режиме смещается ближе к линзе.

Использованная здесь идеализация не позволяет полностью провести расчёты и построить плотности фокального распределения облучённости. Не останавливаясь на подробностях расчёта, опреде­лим основные эффекты при продольных дефокусировках ЛЛФ. Про­дольные дефокусировки приводят к уменьшению фокусного рас­стояния fo до / (a. i) и расширению фокальной линии с образованием пространственных каустик.

Исследовались пассивные системы охлаждения СЭ в составе фотоэлектрических модулей с ЛФ как наиболее простые и дешёвые

[2.9] . Суть эксперимента: КЛФ посылает концентрированный свето­вой поток на СЭ, установленный с хорошим тепловым контактом на радиаторе охлаждения. Схема испытаний и результаты приведены на рис. 2.6. В качестве источника тепла использовались электриче­ские нагреватели, имитирующие поступление солнечной радиации на СЭ, в качестве радиаторов применены алюминиевые листы тол­щиной 1, 2, 3 мм и литые алюминиевые радиаторы, выпускаемые промышленностью.

Используя экспериментальные данные по рис. 2.6, можно по­строить зависимость толщины листа радиатора h от концентрации К при допустимой температуре на СЭ, при этом использовалось эмпи­рическое выражение:

hfol

h =А(К-В)0’5, (2.20)

где размерность А [м], В — безразмерная величина. Для конкретных температур выражение (2.20) получает следующие эмпирические выражения:

t сэ= 60°С; К = 25; h= 1.22 (К-7,3)0’5; tc3=70°C; К = 30; h= 1.36 (К-11,4)0-5; (2.21)

tC3=80°C; К = 38; h= 1.0(К-14)0’5;

1сэ=90°С; К = 45; h = 0,8(К — 15,0)05.

По формулам (2.21) построены графики рис. 2.12.

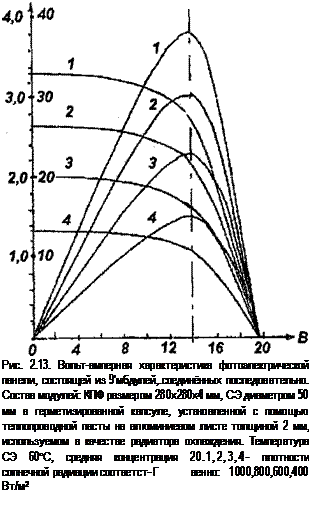
Реализация исследований по пассивным типам термостабили­зации СЭ была выполнена на фотоэлектрических панелях, состоя­щих из 9 модулей (рис. 2.13, 2.14). Концентрические ЛФ размером 280x280x4 мм были установлены на защитном стеклянном листе с тыльной стороны. В фокусах линз установлены СЭ диаметром 50 мм, расположенные в герметичных капсулах из алюминия с защит­ным стеклом. Капсулы прочно прижимались к листу-радиатору толщиной 3 мм через теплопроводную пасту. СЭ были расположены
не в фокальной плоскости (320 мм), а на расстоянии 280 мм, что обеспечивало усреднённую концентрацию 20. Панель устанавлива­лась на следящем стенде и оснащалась необходимым приборным обеспечением для измерения солнечной радиации, температуры на СЭ, температуры воздуха. Общий температурный перепад между СЭ и окружающим воздухом составил 35°С. Таким образом, при экстремальных условиях: температуре воздуха +40°С и радиации 1000 Вт/м2 на СЭ температура составит +75°С.

А Вт

На основе описанных панелей была изготовлена эксперимен­тальная установка пиковой мощностью 300 Вт, представленная на рис. 2.14 (г. Ереван).

Выводы по главе 2

Концентрические линзы Френеля в качестве концентраторов солнеч­ного излучения обладают многими достоинствами: технологичны в изготов­лении, удобное расположение приёмника излучения с тыльной стороны концентратора, возможность получать различные концентрации от несколь­ких десятков до тысяч, возможность формирования облучённости приёмни­ка по необходимому закону.

Приведены формулы расчета геометрических параметров ЛФ.

Исследованы особенности формирования энергетической освещен­ности приёмника излучения, показано, чем отличаются механизмы концен­трирования в линзовых системах от отражательных (рефлекторных) систем.

Рассмотрено влияние хроматических аберраций на концентрирую­щую способность, показано, что для фотоэлектрических систем с СЭ с раз­мерами, значительно превышающими след от элементарного солнечного луча, этим явлением можно пренебречь.

Приведены результаты исследования изготавливаемых промышлен­ностью КЛФ в качестве концентраторов: определение продольных и угловых дефокусировок.

Показана возможность формирования КЛФ с необходимым профи­лем на примере изготовленной линзы.

Рассмотрены вопросы термостабилизации СЭ пассивными средст­вами: алюминиевым листом и оребрёнными радиаторами.

Изготовлены и испытаны фотоэлектрические панели размером ~ 0,9×0,9 м с девятью модулями на основе КЛФ, показана эффективность предложенных систем охлаждения.

Рассмотрим характеристики КЛФ при продольной (вдоль главной оптической оси) и поперечной дефокусировке [2.6, 2.7]. Исследовались серийно изготавливаемые пластмассовые ЛФ квад­ратной конфигурации размером 280x280x3 мм с фокусным расстоя­нием 320 мм и шестигранные линзы площадью 672 см2. Фокусное расстояние по методике, изложенной в [1.16], было уточнено, что показано нарис. 2.6.

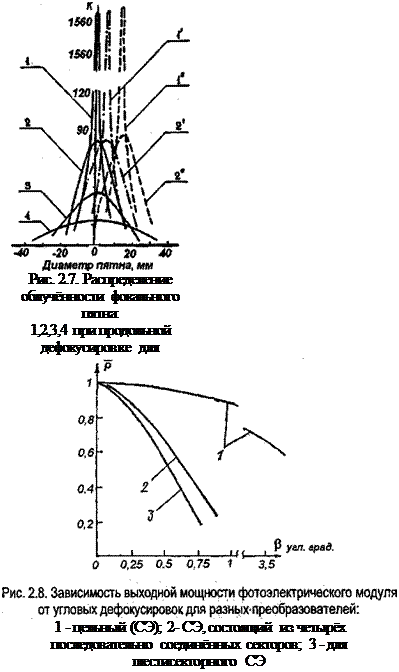
Исследования распределения освещённости проводились на стенде с постоянным слежением за положением Солнца. Для изме­рения освещённости использовался фотоэлектрический солнечный датчик с чувствительной поверхностью 1 мм2 с термостабилизацией, обеспечиваемой металлическим воздушным радиатором. На рис. 2.7 приведено распределение облучённости при продольной дефокуси­ровке на расстояниях от линзы 320, 290, 270 и 250 мм, на рис. 2.8 — угловая дефокусировка для солнечных элементов, выполненных из последовательно соединённых секторов круглого элемента.

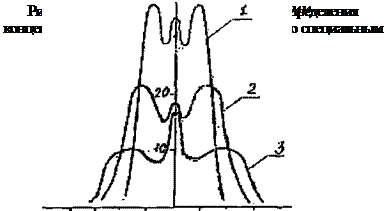
Большим преимуществом ЛФ является возможность форми­рования необходимой облучённости СЭ в фокальном пятне за счёт соответствующего профиля рабочего слоя линзы. На рис. 2.9 приве­дён способ формирования профиля линзы с усреднённой эпюрой облучённости приёмника излучения за счёт того, что рабочие риски профиля линзы имеют одинаковые углы в пределах радиальных зон от Ri до R2; R2- R3 и т. д. Линза с подобным профилем была изготов-
к

40 20 0 20 40

лена и солнечные испытания для различных фокусных расстояний приведены на рис. 2.10 (сравните с концентрацией для светотехни­ческих линз по рис. 2.7).

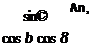При прохождении призматических граней ЛФ солнечный луч разлагается в спектр, при этом элементарный луч в общем случае получает угловое приращение А 8 [2.6]:

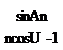где 0 — угол при вершине призмы; b — угол преломления; 8 — угол выхода излучения. Для призм с разными рабочими профилями по отношению к приходящему излучению (по направлению или про­тив) величины А 8 будут разными. Для линз а модификаций угло­вое приращение определяется формулой:

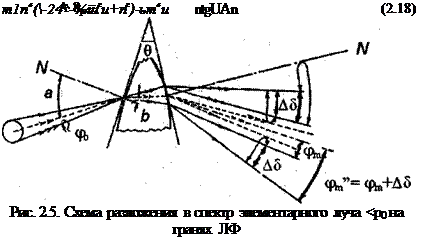Для линз р модификации угловое приращение составит:

Угловой размер элементарного луча после прохождения лин­зы будет:

<Рт = 9т + . (2-19)

где (рт элементарный луч после линзы в монохроматическом пред­ставлении (рис. 2.5).

В гелиотехнических установках учитывать хроматическую аберрацию необходимо только в случаях, когда размеры СЭ соизме­римы с фокальным пятном точечной линзы. Обычно СЭ во много раз превышают по размерам изображение элементарного луча и по­этому хроматические аберрации могут не приниматься во внимание.

Закономерности формирования плотности излучения в фо­кальном пятне линзовой системы отличаются качественно от такого процесса в отражающих системах: угловые размеры элементарного луча, падающего на линзу, не равны угловым размерам преломлен­ного луча и зависят от дисперсии системы [2.4].

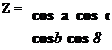Результирующая деформация преломлённых призмой лучей оценивается согласно [2.5] интегральным коэффициентом :

где углы падения а и с (обычно обозначаются і), углы преломления b и б (обычно г).

Для линз с гладкой стороной навстречу падающему потоку a=b=0, а углы с и 5 следуют из построения.

С учётом зависимости конструктивного угла а от апертуры U формула (2.1) может быть записана как

sinU

tg а =———- —. (2.9)

п-COSU

С учётом (2.8) соотношения между угловыми размерами па­дающих и проходящих пучков получаем коэффициент:

где индекс а относит формулу к типу линзы с гладкой стороной на­ружу (рис. 2.1, а).

Таким образом, угловой размер преломлённого луча определя­ется формулой:

фґ Za ф0,

где (р0 — угловой размер падающего солнечного элементарного луча (ф0=16’=4,65 мрад).

Диаметр фокального пятна для концентрических и линейных ЛФ определяется формулой:

Dm = 2f<p0Z/cosU. (2.12)

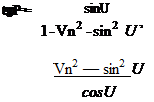Для линз с рабочим профилем навстречу падающему светово­му потоку преломляющие углы рабочего профиля обозначим (3 и соответствующие формулы принимают вид:

На рис. 2.4 приведены графики изменения величин Za, Zp, уг­лов а и р, и коэффициентов концентрации Ка и Кр для условной линзы с коэффициентом преломления п = 1,5.

Практическая ценность интегральных коэффициентов Z со­стоит в том, что при равенстве апертурных углов U линзы модифи­кации р имеют большую концентрацию, чем линзы с гладкой сторо­ной наружу (модификация а). Так, для концентрических (дисковых) линз с U=20° имеем (Кр/Кц )д= 2, т. е. концентрирующая способность линзы в р модификации оказывается в 2 раза выше, чем для а мо­дификации. Для линейных ЛФ (Кр/Ka )л = 1,4, что значит концентра­ция выше на 40%.

Предельную концентрацию в фокусе ЛФ концентрической с точечным фокусом можно подсчитать по формуле (для линз с шагом до 0,5 мм, иначе необходимо учитывать размытие фокального пятна на величину шага):

Ещах = хЕ0(1/ Z2(p02 )sin2Um, (2.15)

где Е0 — прямая солнечная радиация, Вт/м2; т — интегральный коэф­фициент светопропускания ЛФ; фо — угловой радиус, равный 0,004654 рад; Um — угол раскрытия линзы (угловые градусы); Z — ин­тегральный коэффициент для линзы соответствующей модифика­ции.

Определяющим фактором выбора профиля гелиотехнических линз является оптимизация профиля по коэффициенту пропускания

[2.3] . При этом приходится учитывать противоречивые требования:

52

с одной стороны, для улучшения компактности модуля, снижения материалоёмкости и веса желательно уменьшить фокусное расстоя­ние f, т. е. увеличивать параметр Rmax/f, с другой стороны, увеличе­ние этого параметра ограничивается возрастающими светопотерями.

Светопропускание (ті) отдельных граней рабочего профиля (локальный коэффициент) оцениваем по формуле:

Ті (1 Т]) (1 Рфі) (1 Р ф2) (1 Лтех) (1 Лзат) (1 ЛрасХ ( 2.4)

где Tj — поглощение материала грани; рфЬ рф2 — френелевские отра­жения света на входе и на выходе из линзы; цтех — потери технологи­ческие на скругленнях профиля; Цз*,. — потери «затенения» на нера­бочих участках; т]рас — потери на рассеяние.

Поглощение в материале зависит от оптического пути луча в материале и показателя поглощения материала к:

Т, = е ~к|, (2.5)

где к — показатель поглощения материала; 1 — оптическая длина луча.

Френелевские потери на переходе лучей из одной среды в другую определяются по формуле:

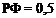s^i)+*!eziil, <2.6,

sm (/’ + !,) tg (/’ + /,)_

где і и U — углы падения и преломления на границе перехода.

Технологические потери ттех определяются рассеянием лучей на радиусах скруглений профиля и регламентируются возможностя­ми технологии изготовления линз. Для пластмассовых линз с шагом 0,5 мм радиусы скруглення г = 0,05 — 1,0 мм.

Потери «затенения» тзат присущи профилю по рис. 2.1, б (свет с рабочей стороны линзы). На рисунке нерабочая зона заштрихова­на, она характеризуется тем, что попавшие в неё лучи не дойдут в фокус из-за «затенения» нерабочей гранью.

На рис. 2.2 приведены локальные значения коэффициента светопропускания т; (светопропускание, определяемое геометри­ей сечения) и углов рабочего профиля а в зависимости от пара­метра R; / f, при этом не учтены потери на поглощение света и технологические, т. к. они не зависят от геометрических парамет­ров профиля.

Для определения интегрального пропускания (т) концентри­ческих линз требуется учесть ценность кольцевых зон профиля по их энергетическому вкладу:

t=^riFi/FJ1,

І

где z — число рабочих граней в линзе; Tj — локальное значение про­пускания і-той грани; F; — площадь светового сечения і-той грани; Fa — площадь светового сечения линзы.

На рис. 2.3 приведены значения интегрального коэффициента пропускания т для кольцевых и линейных линз. Приведённые гра­фики удобно использовать на стадиях проектирования линзового концентратора для выбора основных параметров Rj / f и соответст­вующих ему коэффициентов пропускания.

Рабочий профиль современных гелиотехнических линз Фре­неля (ЛФ) представляет набор призматических элементов, при этом преломляющие способности этих элементов подобраны в соответст­вии с необходимыми принципами формирования освещённости на поверхности приёмника излучения. Основными типами рабочего профиля являются кольцевой концентрический, формирующий све­товой поток в фокальное пятно, и линейный профиль, формирую­щий фокальную полосу [2.2, 2.3].

Рассмотрим построение профилей и схему светопропускания ЛФ нарис. 2.1.

Основные элементы профиля линзы: грань рабочего профиля, определяемая углами а, толщина несущего слоя tH, высота рабочего профиля h, фокусное расстояние f, шаг рабочего профиля s. Расчёт профиля линзы сводится к определению углов сії и атах, соответст­вующих текущим и максимальным значениям расстояния Rj и Rmax радиусов рабочего профиля от главной оптической оси при задан­ном фокусном расстоянии f, коэффициенте преломления материала линзы п, толщинах tH Htp.

Для линзы (рис. 2.1, а) величина а определяется из соотноше­ния:

Для линзы с профилем по рис. 2.1, б величину углов а опре­деляют из выражения

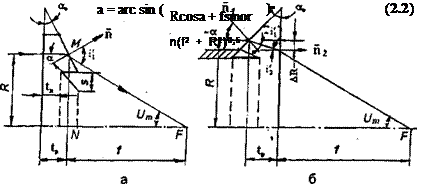а — солнечная радиация приходит с гладкой стороны линзы;
б — радиация с рабочей (профилированной) стороны

При выводе формул (2.1) и (2.2) принято, что размеры приём­ника излучения значительно превосходят величину солнечного изо­бражения в фокусе и можно пренебречь величинами tH и tp.

Максимальное значение и Um для профиля на рис. 2.1, а уста­навливаются по следующему принципу: при увеличении R увеличивает­ся а и при некоторых значениях R^ определяется по формуле:

Rmax = f Ctg (arc Sin — ), (2.3)

n

т. е. на гранях c R^ происходит полное внутренние отражение. Так, для линзы с f = 320 мм, выполненной из органического стекла с п = 1,49, Rmax = 353 мм. Естественно, что для а, близких к углу полного внут­реннего отражения, характерны большие потери, поэтому в реальных линзах наибольшие значения а должны быть меньше

Преломляющие системы (различного типа линзы) имеют одно несомненное преимущество перед отражающими концентраторами в том, что приёмник излучения вынесен на тыльную сторону прини­мающей солнечное излучение поверхности, т. е. не затеняется при­ёмником и его опорами.

К линзовым концентраторам могут быть отнесены следующие устройства:

• концентрические линзы Френеля (КЛФ), выполненные в ви­де набора концентрических преломляющих элементов с прямыми или кривыми образующими рабочих поверхностей;

• линейные (цилиндрические) линзы Френеля (ЛЛФ) с пре­ломляющими элементами в виде треугольных призм;

• дисперсионные линзы Френеля, главным принципом работы которых является разложение света в спектр, для чего подбирают фотоэлектрические приёмники излучения с соответствующей спек­тральной чувствительностью;

• голографические линзы Френеля.

Главной особенностью линзовых концентрирующих систем является наличие хроматических аберраций. В линзах с высокой концентрацией хроматические аберрации уменьшают степень кон­центрации, но при расчёте гелиотехнических линз с концентрацией около 100 ими можно пренебречь. Для дисперсионных линз диспер­сию света увеличивают и строго контролируют.

Преимущества линз Френеля следующие [2.1].

1. Высокая технологичность изготовления линз Френеля (прессовка, прокатка) и относительно низкая стоимость.

2. Высокие конструктивные качества линз как компактных, плоских объектов, удобно монтируемых в несущие конструкции с высокой степенью заполнения занимаемой площади.

3. Удобное для эксплутационных целей взаимное расположе­ние приёмника излучения на тыльной стороне концентратора.

4. Возможность формирования облучённости фокальной плоскости по необходимому закону, что достигается соответствую­щим изменением профиля линзы Френеля.

5. Меньшая, чем для зеркальных концентраторов, необходи­мая точность слежения.