Разработка фотоэлементов, прозрачных за длинноволновым краем основной полосы поглощения, сделала возможным получение се­лективности спектральных оптических характеристик с помощью покрытий, нанесенных на тыльную поверхность этих фотоэлемен­тов, свободную от контактных полос, и почти полностью отражаю­щих нефотоактивную часть солнечного излучения. Это позволяет понизить равновесную температуру не только тех солнечных бата­рей, которые укрепляются на гибкой прозрачной несущей основе, но также и солнечных батарей, монтируемых на металлической поверхности самих космических аппаратов. Недавно было показа­но, что для очень тонких фотоэлементов (70—100 мкм) наличие отражающего слоя на тыльной поверхности полезно также и тем, что большая часть солнечного излучения в основной полосе по­глощения, проходящая сквозь тонкий фотоэлемент, за счет много­кратного отражения от рабочей и тыльной поверхностей в конце концов полностью им поглощается, что приводит к повышению КПД [391.

Рассмотрим специфические вопросы, возникающие при оптими­зации таких селективных систем и покрытий. При расчете не будем учитывать наличия на рабочей поверхности фотоэлемента просвет­ляющих и защитных стеклянных покрытий, которые прозрачны
и весьма слабо влияют на коэффициент отражения кремниевого фотоэлемента в области спектра 1,1—3,0 мкм. Справедливость такого допущения была подтверждена хорошим совпадением рас­четных результатов с экспериментальными, полученными при от­сутствии и наличии покрытий на рабочей поверхности исследован­ных фотоэлементов.

Не будем учитывать также наличия сильнолегированного (кон­центрация примеси порядка 1020 см-3), но весьма тонкого (0,5— 0,7 мкм) диффузионного слоя, поскольку ранее было показано, что такой слой в области спектра 1,1—3,0 мкм прозрачен и не влияет на оптические характеристики фотоэлемента. В связи с этим в расчетах делается допущение, что в спектральной области 1,1— 3,0 мкм кремний характеризуется только вещественным показате­лем преломления. Ограничимся рассмотрением нормального паде­ния излучения па систему.

Коэффициент отражения системы кремниевая пластина — отражающий металлический слой

Амплитуда коэффициента отражения запишется в виде

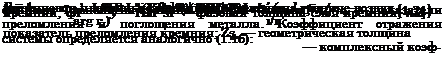= 1„ —^expt—2гф0
0 і +/0гіЄхр(— ггсро ’

где из-за комплексного коэффициента Френеля на границе крем­ний—металл появляется cos (/гщ/щ4л;/?і — arg Гі). Формула коэф­фициента отражения в виде (1.21) применима лишь к оптическим системам, каждый из слоев которых имеет интерференционную тол­щину. В нашем случае толщина кремниевой пластины, обозначен­ная Zsi, много больше “к, а значение фазового угла становится не­допустимо большим и сильно зависит от небольших изменений Is і и X. Поэтому необходимо усреднить R по всем возможным значениям фазового угла.

Окончательное выражение для коэффициента отражения систе­мы имеет вид

Коэффициент отражения системы
кремниевая пластина — антипросветляющий слой
интерференционной толщины —
отражающий металлический слой

Введение антипросветляющего диэлектрического слоя позволяет еще больше увеличить отражение от кремния в выбранной области спектра. Похожий прием — применение одного или двух анти­просветляющих слоев — успешно используется в оптике для повышения отражения в видимой части спектра от стеклянных зеркал со слоем алюминия на тыльной поверхности [401. Длину волны, на которой диэлектрический слой будет антипросветляю­щим для границы кремний—металл, выберем из условия макси­мального отражения наиболее интенсивной части инфракрасного излучения, проходящего до тыльпой поверхности фотоэлемента. Вывод формулы коэффициента отражения для рассматриваемой системы основан на тех же рассуждениях, которые приведены для случая, когда нет антипросветляющего слоя.

Формула коэффициента отражения аналогична (1.22), только в этом случае г является амплитудным коэффициентом отражения при падении излучения из кремния на границу диэлектрический слой—металл. Определяется IrJ2 аналогично |г0|2:

, (2 І /і I2 + I г2 |2 + 2 | /і | | г2 | cos (лд1дАл/Х — arg г2)

1 Гі 1 " 1 + І /і І2 I r2 I2 + 2 I h I |r21 cos (Пцід4лД — arg r2) — ^

nSi —

где /і ———————- коэффициент Френеля на границе кремний—

nSi ‘ ”д

диэлектрический слой, arg/0 = 0; па — показатель преломления диэлектрического слоя; 1Л — геометрическая толщина диэлектри-

42

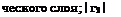
— комплексный коэффици­ент Френеля на границе диэлектрический слой—металл;

Представляет интерес определить оптимальную толщину анти­просветляющего слоя для фиксированной длины волны, чтобы получить возможность рассчитать максимальный коэффициент отражения.

При анализе формул (1.21) и (1.22) находим, что R —> Яшах, когда ) гх |2 —> | |п, ах, а значение | 2 максимально, когда

cos (пдїд4яД — argr2) = 1. Значение | |2 минимально, когда

cos (пд/д4лА — argr„) = —1, т. е.

Условие максимальности | |2, а следовательно, и R запишется

в виде

ид£д4лА — argr2 = + 2ят, где т = 1, 2, 3,…

Следовательно, оптимальная толщина антипросветляющего слоя для получения максимального отражения на выбранной длине волны

В обычной конструкции фотоэлемента инфракрасное излучение, прошедшее сквозь р—«-переход, поглощается сплошным тыль­ным контактом. Очевидно, что для беспрепятственного прохожде­ния излучения сквозь преобразователь тыльный контакт должен. быть выполнен не сплошным, а в виде контактной сетки, занимаю­щей возможно меньше места. В этом случае в базовом слое фото­элемента появляется сопротивление растекания, увеличивающее последовательное сопротивление и уменьшающее КПД. Размеры и конфигурация тыльной контактной сетки должны быть оптимизи­рованы, чтобы замена сплошного контакта на сетчатый не привела к заметному увеличению последовательного сопротивления.

Проведен расчет сопротивления базового слоя фотоэлемента при различных конфигурациях тыльного контакта:

где/гш, Лд — ширина и длина фотоэлемента; — ширина контакт­ной полосы; L — расстояние между контактными полосами на тыльной стороне фотоэлемента; р — удельное сопротивление базо­вого слоя кремния толщиной I.

Второе слагаемое суммы представляет собой последовательное сопротивление базы без учета растекания, первое — дополнитель­ное сопротивление растекания из-за того, что контакт нанесен не на всю поверхность [37]. Произведение hmhA представляет собой площадь фотоэлемента и сплошного контакта.

В результате расчета определено сопротивление базового слоя /?Г) (Ом) при различных конфигурациях тыльного контакта:

Удельное сопротивление р материала базы кремниевого фото­элемента принималось равным 1 Ом-см, толщина базы 0,05 см, площадь 10 X 20 мм, ширина контактной полосы на тыльной стороне 0,2—0,3 мм, что позволяет не учитывать сопротивление самих контактных полос.

Как видно, при контакте по периметру и с тремя поперечными полосами, занимающем всего 7—10% площади, сопротивление базового слоя практически такое же, как при сплошном тыльном контакте.

Небольшого увеличения температуры прибора из-за того, что 7—10% площади тыльной поверхности будут заняты контактами и вследствие этого непрозрачны для инфракрасного излучения, можно избежать, нанося в тех же местах аналогичную контактную сетку на рабочую поверхность. При нанесении контактных сеток методом фотолитографии такое совмещение не представляет техни­ческих трудностей. Контактная сетка на рабочей стороне может быть затем покрыта (электрохимически или испарением в вакууме) слоем металла, обладающим высоким коэффициентом отражения в области солнечного излучения, например алюминием или сереб­ром.

Полное последовательное сопротивление фотоэлемента Ra состоит из сопротивления растекания легированного слоя Лл, сопротивления базы Rq и переходного сопротивления контактов металл—полупроводник R,{:

Rn — Rn + Вб + Як

В работе [38] было показано, что КПД фотоэлемента начинает заметно уменьшаться, если последовательное сопротивление Ra становится больше 1,5—2,0 Ом. Нанесение на рабочую поверхность контактных полос с шагом 4—5 мм или сетки с ячейкой 10 X 10 или 5 X 10 мм позволяет уменьшить сопротивление растекания легированного слоя толщиной 1—1,5 мкм до долей ома. Переход­ное сопротивление контактов металл—полупроводник у серий­ных фотоэлементов благодаря операции термообработки состав­ляет сотые доли ома.

Таким образом, при тыльном контакте по периметру и с тремя поперечными полосами вклад сопротивления базы (0,07 Ом) в общее последовательное сопротивление незначителен. Общее по­
следовательное сопротивление фотоэлемента, прозрачного в ин­фракрасной области солнечного спектра, не будет выше 0,5 Оді, что позволит электрическим параметрам остаться на исходном уровне параметров непрозрачных фотоэлементов со сплошным контактом.

Результаты расчета хорошо согласуются с экспериментом (см. главу 2). Дальнейшее усовершенствование конструкции фотоэле­ментов, прозрачных в инфракрасной области солнечного спектра, показало, что они могут быть созданы и из таких полупроводнико­вых материалов, как монокристаллический арсенид галлия, и из поликристаллических пленок гетеросистемы Cu2S—CdS. Кроме этого, использование фотолитографии позволило получить кон­тактные сетки, занимающие не более 5% площади как рабочей, так и тыльной поверхностей фотоэлементов при ширине полос 0,03—0,05 мм и расстоянии между ними 1—2 мм. Это привело к получению общего последовательного сопротивления таких фотоэлементов, не превышающего 0,08—0,1 Ом даже при толщине легированного слоя менее 0,5 мкм.

1.4.

Прежде всего необходимо было выяснить, какая часть инфра­красного излучения поглощается в легированном слое различной толщины со среднеслоевой концентрацией свободных носителей заряда (1 — і — 2)-102° см-3, поскольку базовый слой фотоэлементов с концентрацией носителей заряда 1016 см-3 [30] при толщине, характерной для фотоэлементов (200—500 мкм), несомненно, прозрачен для инфракрасного излучения. Трудность оценки влия­ния легированного слоя на коэффициент пропускания фотоэле­ментов состояла в том, что в литературе отсутствуют данные по оптическим константам п (к) и к (к) сильно легированного крем­ния (концентрация носителей заряда выше 2-Ю19 см-3). В связи с этим нами были определены оптические константы в сильнолеги — роваппом кремнии. При этом было сделано допущение, что силь­нолегированный слой фотоэлементов легирован равномерно по всей глубине и имеет концентрацию примеси, равную 2-Ю20 см-3.

Расчет был проведен в соответствии с методикой, предложенной в работе [35]:

/ Се2 •

El —• Єо — •

+ [(-£ЗШ*+2<*-*>ГЬ

Коэффициент отражения сильнолегированной полированной поверхности R (к) кремниевых фотоэлементов был тщательно изме­рен в интервале спектра 1,0—3,0 мкм, и полученные данные ис­пользованы в расчетах.

Вычисленные по приведенным выше формулам значения опти­ческих констант п (Я) и к (X) слоя сильнолегированного кремния (до концентрации 2-1020 см-3) представлены в табл. 1.4.

Следующий этап расчета состоял в выводе формул для коэф­фициентов пропускания и отражения кремниевого фотоэлемента.

Представим фотоэлемент в виде двухслойной системы без ка­ких-либо просветляющих и контактных слоев: тонкий слой сильно­легированного кремния — базовая область. В такой системе сильнолегированный слой имеет интерференционную толщину и комплексный показатель преломления, а базовая область — не­интерференционную толщину и вещественный показатель прелом­ления. Как показывают расчет и эксперимент, полированные с обеих сторон кремниевые пластины толщиной 200—500 мкм с удельным сопротивлением 1,0 Ом-см практически не обладают поглощением в области спектра 1,1—3,0 мкм.

Амплитудный коэффициент пропускания системы запишется в виде

f = g«h exp (— ttPi)

0 1 + /(A exp (— ї2фі) ’

2л

где фх == — т— Іл{Щі — ікя); Ія, пя, кл — фазовая толщина, геометри-

ческая толщина, показатели преломления и поглощения сильноле- гированного слоя кремния соответственно.

Коэффициент пропускания системы определяется как | 12 =

= t<,t*, гДе *о — величина, сопряженная t„, т. е.

h |2 = | go I21 /і |2 exp(— Лтлгл4яА)/[ 1 + 1 /оГ | А|2ехр (—Алгл8я/А,) + + 21 /о | | а | cos (пл1лАп/К — arg/0 — arg а) ехр (— кл1лАя/К)]. (1.18)

Здесь коэффициенты Френеля на границе воздух—сильнолегиро — ванный кремний

_________________ 2 п0 .

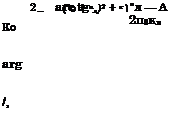ё° «о + »л-і/сл ’

Амплитудный коэффициент пропускания на границе сильнолегиро­ванный кремний—базовый слой кремния

А*гехр(— in6l62nfk) tx ~ 1 + /ігг exp (— ія6!б4яА) ’

амплитудный коэффициент отражения на той же границе _ /і + г2 ехр (— ІП6ІбАл/Х) _

Гі ~~ 1+ / 1Г2 ехр (— і6пбІб4п/1) ’

и I2 ___________________ I 12 I ‘г Iа_____________________

1 + І /і Iа Іг2 Iа + 2 I /j 11 r2 I COS (лб*б4яД — arg /, — arg r2) >

I /1 Iа + І г2 Iа + 2 I /„ I I r2 I cos (nal6in/k + arg fr — arg r2)

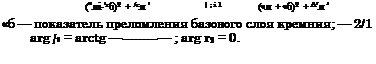1 — г І /і Iа I r2 I2 + 2 I /j I I r2 I cos (ибгб4лД — arg /, — arg r2) ’ где коэффициенты Френеля

Значения t2 и r2 находятся из граничных условий через коэффици­енты Френеля на границе кремний—воздух:

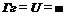2л л

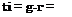«6 +"о ’

Толщина базового слоя кремния во много раз больше толщины слоя силыюлегированного кремния и является неинтерференцион­ной, так как Iq Я. Так как ср = лб/й4я/Я сильно зависит от не­больших изменений 15 и Я, формулы не отражают действительной физической картины взаимодействия излучения со средой. Поэто­му необходимо усреднить | J2 И I | ^ по всем возможным значе­ниям <р, т. е. по периоду 2л.

Запишем | t1|2 и | гх| 2 в виде

І, 12 _ _______________ І*і Iа! «2 Iа_____________ .

111 ‘ ‘ + l/il*|r*|* + 2|/1| 1 ra I cos (ф — Р) ’

I _ I* _ І /і I2 + 1 г-212 — Ь 2 I /г | |г2|Соя(ф + Р)

1 11 і-і-І/іІЧгаР + гіПІ 1Г*|С08(Ф-Р) ’

где р = агgfL.

Учитывая, что cos (ср — 3) — cos ср cos [3 + sincpsin р, обозначим

а = 1 + | /112 |г212; Ь= 2П |r2|cosp; с = 21 f, | | г, | SLn р.

Тогда

к, |* =________ Щ’М_____________ .

11 а + Ь cos ф + с sin ф ’

2Л 2П

о о

Необходимо вычислить интеграл

2Я

1 I" __________ Йф________

2л j а + b cos ср — f — с sin ф ’ о

если а2 — Ъ2 — с2 0.

В данном случае

а*_Ь*_с2 = 1 + 1/і|1|Г2|4+2|/1|2|г2|2- — 41 /і I2 I r212 (cos2 P + sin2 P) = (1 — I ft I21 r212)2 > 0.

Заметим, что при ср = л производная меняет знак, поэтому необходимо обойти эту точку по дуге малого радиуса 6, а затем принять 6 —»• 0:

2Я Я—6

_±_ С _______ <*ф_______ = С <*ф_ ,

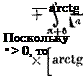2л J а + b cos ф с sin ф j а + Ъ соа}ф + с sin ф о п

2Я

1 С _____________ йф________________________ 1______

2л J а 4- b cos ф 4- с sin ф (а2_________ ь2__ с2)1^2

о v ‘

Подставив значения а, Ь и с, получим

__________ 1___________ ______ _________ 1

(я2 — Ь2 — (2)1/2 1 — I h I2 I r2 I2

Таким образом,

I. і 2 _ I Si I21 h I2

Iі! I yep — 1 _ |/г |2 j r2 j2 ■

После усреднения по всем возможным значениям ф при усло­вии а -(■ Ъ cos ф с sin ф 0 выражение для 1^1® примет вид

і. и 4 (1 — І /і I*)(1 — Iг*I*) — 41 Л |*|г.|*sin»(arfr/,)

1 1|уср " 1-І h І2 Іг212 •

Докажем справедливость неравенства а + b cos ф + с sin ф > 0.

Произведя замену переменной х = tg (ф/2), получим

или

(а — Ь) х2 + 2сх1 + а Ъ 0.

Поскольку

а*_6*-с* =(1 -|Л I2 f r2 J2)2 > 0, дискриминант квадратного трехчлена отрицателен

4с2 — 4 (а2 — Ь2) < 0.

В силу того, что а Ь, исходное неравенство выполняется при любых значениях ф.

Вернемся теперь к определению J г01 2 (1.18). Заметим, что arg Г! по вышеуказанным причинам сильно зависит от малых изменений X и /б, следовательно, чтобы получить коэффициент про­пускания Г, необходимо |10| 2 усреднить по всем значениям arg?^, т. е. по периоду.

Обозначил:

1лпл — arg /о = фл; arg гх = Pi.

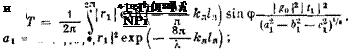Далее везде вместо 1^1 и | П| используются значения | уср

а — Ъ — с = 1 + | /о |41 и |4 exp (— Алгл16я/А.) 4- + 2 f /„ I* I r, Iа exp (- каІя8яД) — 41 /о І21 Гі I® x X exp (— клІл8п/К) (cos2 P) + sin2 pt) =

= [1 — І /о I2 b I2 exp (— /сл/л8яА))2 > О.

В окончательном виде коэффициенты пропускания и отражения всей системы

I go I2! h I2 exp (— каІлАп/к) 1-|/о|2Ы2ехр(- *пІл8лА) [2]

R = 1 —

_ (1-І /о |2)[1—к I2 exp (—А-лгл8лД)]-4 І /о I2 I г, I® exp (—Vj8nA)sin®(arg /„) _ і — I to I2 I ri Iа exp (— кліл8л/Х)

(1.20)

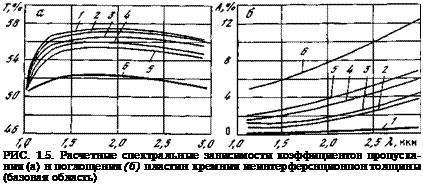Используя выведенные формулы (1.19) и (1.20), рассчитанные оптические константы сильнолегированного слоя (см. табл. 1.4) и известные константы базовой области [30], можно определить спектральные зависимости коэффициентов отражения R, пропуска­ния Т и поглощения А (А = 100%—R — Т) для различных значений толщины сильнолегированного слоя. Полученные рас­четные данные представлены на рис. 1.5, из которого видно, что пропускание и поглощение фотоэлемента сравнительно слабо отличаются от пропускания и поглощения чистого кремния при толщине сильнолегироваиного слоя менее 1,0 МІШ.

Таким образом, для получения максимальной прозрачности фотоэлемента необходимо уменьшать толщину легированного слоя, и это требование совпадает с основной тенденцией в улучшении электрофизических характеристик фотоэлементов, поскольку при уменьшении глубины залегания р — «-перехода большая часть света поглощается в базовом слое с большой диффузионной длиной, что приводит к увеличению коэффициента собирания и КПД преобразования солнечной энергии. Из расчетов, проведенных, например, в работе [36], видно, что при уменьшении глубины залегания перехода с 2,0 мкм до 0,5 мкм выходная мощность может быть увеличена на 30—70% (в зависимости от профиля концен­трации примеси в легированном слое). Из рис. 1.5 ясно, что такое уменьшение глубины залегания перехода позволяет также на 7— 9% уменьшить поглощение инфракрасной радиации с длиной вол­ны 2—2,5 мкм.

Теоретически и экспериментально удалось показать, что конст­рукция полупроводниковых фотоэлементов может быть оптимизи­рована таким образом, что практически вся инфракрасная часть солнечного излучения за краем основной полосы поглощения полупроводника (для кремния от 1,1 до 2,5 мкм) начнет проходить беспрепятственно сквозь фотоэлемент. Солнечное излучение с к 1,1 мкм будет поглощаться в полупроводнике во многом благодаря эффективным просветляющим покрытиям, а для тепло­вого собственного излучения с к > 3 мкм поверхность фотоэлемен­тов будет высокоизлучающей из-за свойства верхнего слоя оптиче­ского стекла поглощать в области спектра к 2,5 мкм. Такая селективность по спектру интересна не только своей сложностью и необычностью, но также и тем, что для ее получения необходимо использовать не только селективные оптические покрытия, но и сделать селективно прозрачным сам активный элемент преобразо­вателя солнечной энергии — полупроводниковый фотоэлемент.

Подобный подход потребовал проведения детальной теоретиче­ской оптимизации не только оптических, но и электрофизических свойств фотоэлементов, поскольку необходимо было добиться требуемой селективности без ухудшения КПД преобразования солнечной энергии.

Расчет целесообразно начать со случая использования наиболее распространенных кремниевых солнечных элементов без приклеи­ваемого защитного стекла, когда внешней средой служит воздух с показателем преломления п0 = 1 (при применении солнечных

элементов в качестве индикаторов излучения, в системах ориента­ции, для питания малогабаритных радиоприемников и т. д.). Исходными характеристиками при расчете служили спектральная зависимость коэффициента отражения и спектральная чувстви­тельность (отношение тока короткого замыкания при данной длине волны к единице падающей энергии излучения) непросветленного кремниевого фотоэлемента с полированной поверхностью и глуби­ной залегания р — п-перехода менее 1 мкм и повышенной чув­ствительностью в коротковолновой области спектра (рис. 1.1).

Более подробно методика расчета эффективности просветления фотоэлементов описана в главе 2. Здесь лишь укажем, что по виду кривых отражения после просветления (особенно многослойного) возможно оценить прирост КПД фотоэлементов. Самым объектив­ным методом оценки, на наш взгляд, служит сравнение спектраль­ной чувствительности фотоэлементов с различными просветляющи­ми покрытиями после того, как спектральная чувствительность просветленных фотоэлементов пересчитана с учетом распределения энергии в спектре данного источника излучения, например в спектре внеатмосферного Солнца, и определено увеличение интегрального тока фотоэлементов при освещении этим источником излучения.

Была рассмотрена возможность использования для просветле­ния двухслойных систем с кратными значениями оптической тол­щины слоев, полученных в результате оптимизации [28]. При выполнении указанных в работе [28] соотношений между показате­лями преломления слоев многослойных покрытий на кривой отражения можно получить один или несколько минимумов, где коэффициент отражения равен нулю. Расчеты спектральных характеристик в работе [28] были проведены для стекла (показа­тель преломления пст ~ 1,51) в видимой области спектра и для гер­

мания (пос = 4,0) в средней инфракрасной области спектра, но качественно результаты расчетов могут дать представление о харак­тере распределения коэффициента отражения кремния в видимой и ближней инфракрасной области после просветления аналогич­ными покрытиями.

Решение уравнений, определяющих коэффициент отражения поверхности с двухслойным покрытием при одинаковой оптической толщине обоих слоев, позволило определить два оптимальных соотношения между показателями преломления слоев:

nln3 = пп0 (1.11)

и

?г1п2 = п0п3, (1.12)

где и1, /г2, п3, По — показатели преломления внешней и внутрен­ней просветляющих пленок, подложки и внешней среды (воздух) соответственно.

При оптической толщине каждого слоя, составляющей нечетное число A. mj„/4, гдеЯщіп — длина волны, соответствующая минимуму коэффициента отражения, выполнение соотношения (1.11) позволя­ет получить кривую отражения с одним нулевым минимумом. При выполнении соотношения (1.12) могут быть получены два нулевых минимума на спектральной кривой отражения, причем в точке максимума (между этими двумя минимумами) оптическая толщина каждого слоя равна Хтаї/4.

Расчет показывает, что если пг принять равным 2,8 при X = = 0,6 мкм, как у пленок двуокиси титана ТЮ2 (значение показате­ля преломления кремния при этой длине волны в соответствии с данными работы [30] составляет 3,94), то для выполнения соотно­шения (1.11) показатель преломления внешней пленки двухслой­ного покрытия пг должен быть равен 1,4. Напомним, что /iMgF„ = = 1,38 и nSio, = 1,45.

Соотношение (1.12) выполняется, если пг = 1,6, пг = 2,5. Однако такое двухслойное покрытие будет давать значительное отражение в точке максимума отражения между двумя нулевыми значениями. Значение коэффициента отражения после нанесения двухслойного покрытия в максимуме может быть рассчитано по формуле

/ пп3 — npi0 ,‘-

ЛХ/4 = |——- ;—п— ‘

V 4- ппо ‘

В работе [28] подробным расчетом спектральных кривых отраже­ния германия (п$е = 4,0) в инфракрасной области спектра было показано, что величину максимума коэффициента отражения можно значительно снизить, выбрав пленки с пх = 1,35 и щ = 2,3 вместо п1 — 1,6 и щ = 2,5. Вся кривая отражения располагается ниже,

хотя нулевые значения коэффициента отражения не наблюдаются при этом ни в одном из двух минимумов. Очевидно, что для реше­ния нашей задачи — получения низкого значения коэффициента отражения в широкой области спектральной чувствительности солнечных элементов такое двухслойное покрытие является наиболее подходящим. Из проведенных предварительных оценок ясно, что наиболее широкую область низкого отражения для полу­проводникового материала с высоким показателем преломления можно получить, используя двухслойное просветляющее покрытие, у которого ближний к полупроводнику слой имеет показатель пре­ломления п% = 2,3, а внешний — = 1,35 — г-1,4. В случае, когда

оптическая толщина каждого слоя равна Я./4, при длине волны к будет наблюдаться небольшой максимум коэффициента отражения.

Проведен расчет спектральной кривой отражения кремния после просветления двухслойным покрытием из пленок сернистого цинка (п%пs = 2,3) и фтористого магния («MgF2 — 1,38) различной оптической толщины. Для сравнения был проведен расчет коэф­фициента отражения кремния после просветления однослойными покрытиями из ZnS и моноокиси кремния SiO, а также двухслой­ными покрытиями из SiO (nsio = 1,9) и MgF2. В расчетах учиты­валась дисперсия показателей преломления Si и пленок ZnS и SiO [30—32]. Некоторые из использованных в расчетах значений показателей преломления Si, ZnS и SiO представлены в табл. 1.1.

Расчет проведен с использованием рекуррентных соотноше­ний для амплитудного коэффициента отражения [21, 22]. Для двухслойной системы, изображенной па рис. 1.2, были использова­ны расчетные формулы (вывод их из уравнений Максвелла дан в 1.1):

/о + Г, ехр(—2іф!) .

° і + /огі ехР (— 2іфі) ’

/і + Г2ехр(— 2Дрг)

1 1 +/lr2 ехр (-2іфг) ’

где г о — амплитудный коэффициент отражения, соответствующий границе воздух — верхний слой просветляющего покрытия; rt — амплитудный коэффициент отражения на границе верхнего и нижнего слоев просветляющего покрытия.

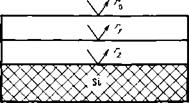РИС. 1.2. Схема двухслойного про­светляющего покрытия на кремнии (без внешнего слоя стекла)

Френелевские коэффициенты отражения на границах сред—

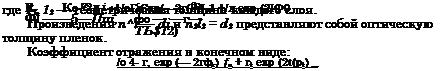где п01 rclt п2, пз — показатели преломления воздуха, внешнего и внутреннего слоев покрытия и кремния соответственно. Фазовая толщина пленок:

І /о I2 + I ri I2 + 2 І /о I 1 Г11 cos («A43T//Q 1 + І /о І21 гі I2 + 2 | /„ I I ri I cos (iiiliiлД)

Полученные в результате расчетов спектральные зависимости коэффициента отражения кремния с двухслойными покрытиями представлены на рис. 1.3. Для сравнения приведены расчетные кривые отражения после нанесения однослойных покрытий ZnS и SiO. Сравнение кривых показывает, что наиболее широкую об­ласть низкого отражения удается получить с помощью двухслой­ных покрытий из пленок ZnS и MgF2. Этот вывод подтверждается расчетом плотности тока короткого замыкания /„.3. фотопреобра­зователей на внеатмосферном Солнце после уменьшения коэф­фициентов отражения в соответствии с кривыми рис. 1.3. Результа-
/?,

fff

4а

sa

га

га

о

4а sa га /а о

sa га аа о

4а

sa

га

га

о

га ла о

а,4 а, а а, а а, г а,8 а, а /,а /,г а, г

Я, мкм

ты расчетов сведены в табл. 1.2, из которой видно, что двухслойное покрытие из пленок ZnS и MgF2 дает возможность приблизительно на 10% увеличить интегральный ток фотоэлементов но сравнению с разработанными ранее однослойными покрытиями из ZnS и SiO 133, 34] и на 5% по сравнению с двухслойными покрытиями SiO+ +MgF2. При форме вольт-амперной нагрузочной характеристики фотоэлементов, близкой к прямоугольной (что характерно для приборов с резким барьером на р — га-переходе и низким по­следовательным сопротивлением), возрастание КПД при просвет­лении соответствует росту тока короткого замыкания, что было обнаружено экспериментально. Поэтому следует ожидать увеличе­ния КПД солнечных батарей примерно на 50% при использовании двухслойных просветляющих покрытий ZnS+MgF2.

Низкое отражение (менее 1%) получено при использовании этих покрытий в интервале спектра от 0,5 до 1,1 мкм (рис. 1.3), т. с. почти во всей области спектральной чувствительности фото­элементов (см. рис. 1.1). Из этого следует вывод, что данное покры­тие является наиболее эффективным просветляющим покрытием для солнечных батарей, работающих в условиях, когда внешний слой лака или стекла не требуется.

Предварительный расчет для случая, когда внешним слоем просветляющих покрытий является полубесконечный слой защит­ного лака или стекла, был проведен с использованием выведенных в работе [28] соотношений между показателями преломления много­слойных покрытий, приводящих к появлению на спектральных кривых точек нулевого отражения, и с заменой внешней среды с п0 = 1,0 (воздух) на среду с п0 = 1,5, что характерно для боль­шинства полимерных прозрачных лаков и неорганических стекол. Следует отметить, что рассматриваемый случай является основным для современного применения солнечных элементов.

Оптимальный показатель преломления просветляющего слоя в случае двухслойного покрытия пленка — стекло определяется из соотношения

п = п0п3.

При X = 0,6 мкм и п0 = 1,5 будем иметь Hj = 2,45.

Напомним, что «zns = 2,34 при X = 0,6 мкм, но при X = = 0,4 мкм уже равен 2,56 (см. табл. 1.1), в связи с чем эта про­светляющая пленка является оптимальной в данном случае.

Для трехслойных покрытий — два просветляющих слоя и стекло — расчет должен быть проведен по формулам (1.11) и (1.12) с заменой п0 = 1 на п0 = 1,5.

Расчет по формуле (1.11) при п0 = 1,5, п3 = 4 показывает, что если задать п2 = 2,7, то тгх должен составлять 1,65, если же п2 = = 2,5, то п1 = 1,53. Это означает, что любое покрытие этого типа не будет лучше, чем двухслойное покрытие с пленкой, имеющей п = 2,3, и верхним слоем из стекла или лака (этот вывод затем был подтвержден экспериментально).

Расчет по формуле (1.12) при па = 1,5, п3 = 4 и п2 = 2,6 показывает, что пг должен быть равен 2,3. Однако величина макси­мума между двумя минимальными значениями на кривой отраже­ния, которая может быть подсчитана по формуле (1.13), будет в этом случае значительной (12,5%). Вероятно, более пологой кри­вой с размытым максимумом можно добиться использованием двух просветляющих пленок с меньшими показателями преломления. Поэтому при расчетах спектральных характеристик были исследо­ваны также трехслойные системы, имеющие просветляющие слои с показателями преломления 2,6 и 2,3, а также 2,3 и 2,1; 2,3 и 1,9; 2,3 и 1,7.

Показатели преломления трехслойных покрытий должны отве­чать соотношению

7грг3 = nl = п0п4, (1.17)

если оптическая толщина каждого из трех просветляющих слоев равна Amin/4. При выполнении соотношения (1.17) трехслойное покрытие должно характеризоваться широкой областью низкого отражения и тремя нулевыми минимумами на спектральной кривой коэффициента отражения — центральным при Amin и по одному с каждой стороны от Amln. Если выбрать в качестве Amin, например, X = 0,77 мкм (учитывая, что область низкого отражения будет широкой) и при этом п0 = 1,5, щ = nsi = 3,7, то соотношение (1.17) будет удовлетворяться при п3 = 2,6, п2 = 2,35, щ = 2,1, что совпадает с показателями преломления просветляющих пленок Ті02, Се02 (или ZnS), Zr02. Близкие по характеру кривые отраже­ния позволяют получить покрытия с соответственно уменьшенными показателями преломления, хотя коэффициент отражения в мини­мумах в этом случае не будет равен нулю.

Расчет многослойных покрытий упрощается, если оптическая толщина какого-либо из слоев кратна Х/2— наличие такого слоя не сказывается на значениях показателей преломления остальных слоев, которые в этом случае могут быть найдены, например, для четырехслойных покрытий по соотношениям, полученным для трех­слойных покрытий и т. д. Это открывает возможность использова­ния в качестве слоев с толщиной, кратной Х/2, пленок с низкими показателями преломления. При этом значительно упрощается процесс нанесения многослойных покрытий, так как наибольшую трудность при экспериментальном воспроизведении представляет получение прозрачных слоев с высоким показателем преломления. Однако, как это было обнаружено при расчетах и экспериментах, крутизна минимумов и максимумов кривой коэффициента отраже­ния при этом резко увеличивается, и для снижения отражения в широкой области спектра такие покрытия в большинстве случаев непригодны.

С помощью специально составленной программы для электрон­но-вычислительной машины были рассчитаны многослойные покры­тия не только с различным количеством слоев, но и с различными значениями оптической толщины каждого слоя, в том числе и с не кратными Amin/4. Однако для разработки хорошо воспроизводи­мой технологии просветления наибольшее значение имели такие покрытия, толщина каждого слоя которых кратна A, min/4. Их расчету и было уделено наибольшее внимание.

Показатели преломления пленок выбирались с таким расчетом, чтобы они совпадали с показателями преломления слоев, которые можно нанести экспериментально, а все покрытие в целом представ­ляло бы собой ступенчатую систему, в которой показатели пре­ломления слоев уменьшаются последовательно от кремния до внешнего слоя — стекла.

Просветляющие покрытия с большим числом слоев не рас­сматривались, так как их нанесение в условиях серийного произ­водства фотоэлементов, что важно для развития солнечной энерге­тики, неоправданно усложнило бы технологию.

Расчет спектральных кривых проводился с помощью рекур­рентных соотношений, аналогичных соотношению (1.14), число
которых было равно числу слоев в выбранных для расчета покры­тиях. Коэффициенты Френеля определялись на каждой границе раздела. Каждый из слоев считался прозрачным, и показатели преломления были вещественными.

Наличие внешнего полубесконечного слоя лака или стекла требовало усреднения коэффициента отражения по фазовому углу (иначе фазовой толщине внешнего слоя) в формуле (1.16), примени­мой лишь к оптическим системам, каждый из слоев которых имеет интерференционную толщину. В рассматриваемом случае толщина слоя лака или стекла, обозначаемая 1г (на практике составляю­щая 120—150 мкм), много больше длины волны X. Значение фазово­го угла ер! = становится при этом недопустимо большим

и сильно зависящим от небольших изменений 1Х и X. Это означает, что формула (1.16) не отражает реальной физической картины взаимодействия световых пучков в рассматриваемой системе, содержащей слой неинтерференционной толщины. Чтобы обойти указанную неточность, было необходимо усреднить коэффициент отражения по всем возможным значениям ф1; т. е. по периоду от 0 до 2 л. В результате усреднения, как будет подробно показано в 1.3,

(I —|/о Iі) (1-І г, Р)

1-|/„12К I2

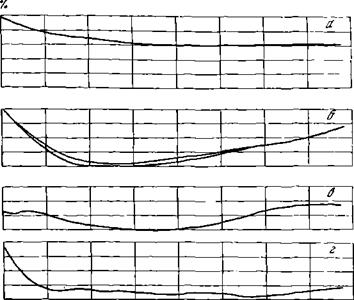
Некоторые из полученных расчетным путем спектральных зависимостей коэффициента отражения представлены на рис. 1.4. Используя расчетные кривые, спектральную чувствительность, типичную для серийно выпускаемых кремниевых фотоэлементов (см. рис. 1.1), пересчитали на плотность тока короткого замы­кания при работе в условиях внеатмосферного солнечного излуче­ния. Расчет был проведен на электронно-вычислительной машине. Результаты расчета многослойных просветляющих покрытий (для случая, когда внешним слоем является полубесконечный слой стекла или лака) приводятся в табл. 1.3.

Из данных табл. 1.3 можно сделать вывод, что трехслойные по­крытия с п3 ~ 2,3, п2 = 1,7, пг = 1,5 или шестислойные покры­тия из слоев с /г6 = 2,6 или 2,7, пъ = 2,3, п4= 2,1, па — 1,9, п2 = 1,7, = 1,5 обеспечивают увеличение тока короткого замы

кания практически такое же, как двухслойное покрытие из пленки ZnS (I = 600 А) и стекла. Этот вывод имеет большое практическое значение. Он означает, что не нужно усложнять технологию про­изводства фотоэлементов из кремния с гомогенным р—и-перехо — дом, вводя в нее нанесение четырех-, пяти — или шестислойных покрытий. Между полупроводником и внешней средой с показа­телем преломления п = 1,5 достаточно создать просветляющую пленку ZnS с геометрической толщиной около 600 А, чтобы почти

на 45% увеличить ток короткого замыкания и КПД фотоэлемен­тов.

В заключение необходимо отметить, что основной целью данно­го раздела было изложение методики расчета эффективности просветляющих покрытий для полупроводниковых фотоэлементов. Совершенно очевидно, что при изменении исходных данных (кри­вой отражения и спектральной чувствительности фотоэлементов, приведенных на рис. 1.1), например при уменьшении глубины залегания р — «-перехода, замены полированной поверхности на микрорельефную или использовании для создания фотоэлемен­тов других полупроводниковых материалов вместо кремния, например арсенида галлия GaAs или сульфида кадмия CdS, резуль­таты конкретных расчетов, приведенные в табл. 1.2 и 1.3, примут

Таблица 1.3

Расчетная эффективность многослойных просветляющих покрытий
кремниевых фотоэлементов

(верхний слой — прозрачное стекло или лак непнтерференцнонной толщины

с л, = 1,5; и„= 1; АМО)

другие значения. Важен основной вывод: описанная здесь методи­ка расчетов позволяет объективно определить оптимальные про­светляющие покрытия для любых разновидностей полупроводни­ковых фотоэлектрических преобразователей солнечного излучения в электрическую энергию.

1.3.

Определение коэффициентов отражения, пропускания и погло­щения многослойной системы с точки зрения электромагнитной теории сводится к решению граничной задачи, т. е. к определе­нию стационарных амплитуд векторов напряженности электриче­ского и магнитного полей на всех границах многослойной системы при падении световой волны с определенными характеристиками. Все энергетические соотношения и фазовые изменения выража­ются через векторы поля [27].

Будем рассматривать случай нормального падения света и выведем для него основные соотношения. Затем с помощью вве­дения соответствующих обозначений и определений эту форму решения сделаем пригодной и для расчета наклонного падения.

Допущения: 1) падающий свет описывается линейно-поляри­зованной монохроматической плоской волной; 2) ширина пучка много больше длины волны.

Первое допущение не ограничивает общности задачи. Второе же допущение о ширине луча исключает дифракционные эффекты.

Оптические свойства каждого слоя полностью описываются комплексным показателем преломления Nj = n;- — ikj (у = 1, 2, З, . . ., ш + 1) и геометрической толщиной lj. Величина kj может быть равна нулю, если в слое пет поглощения.

Внутри многослойной системы возникают интерференционные эффекты вследствие существования отраженной и прошедшей волн в каждом слое, за исключением последней, полубесконечной среды (в том числе полностью поглощающей в данной области спектра), где существует только прошедшая волна. Последнее обстоятель­ство обеспечивает граничное условие для решения уравнений Максвелла в (т + 1)-й среде.

Можно показать, что в случае нормального падения векторы электрического и магнитного полей для всех волн в каждом слое перпендикулярны друг другу и направлению распространения и, кроме того, волны однородны. Последнее означает, что электри­ческое и магнитное поля имеют только компоненты, параллельные границам раздела, и что плоскости постоянной амплитуды и пло­скости постоянной фазы в любом поглощающем слое совпадают.

Решение уравнений Максвелла для электрического и магнит­ного полей в у-м слое запишется в виде

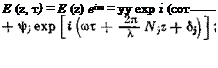(1.1)

Я (Z, т) = я (z) eimT = Nj |vj exp [i (cot——— NjZ + j —

-^exp [г (cor+ b yvjz + 6j) ]} , (1.2)

где t время; z — координата в направлении распространения излучения; у}, г|)у, £г, 6— постоянные, которые выбираются из условий непрерывности Е (г) и Н (z) на каждой границе раз­дела.

Это означает, что

У і ехР [* — -1ГNizi) ] + Ф) ехР [ ■1 («і + — Т — NjZj) ] =

= Tj+i ехР (іл-i———————— 5T~^+lZj)]

+ tj+iexp [і (б;Ч1 + -^L^j+1z/)] ; (1.3)

Nj |vjexp [і fa — -^LyVjZ,-)] — ifcexp [і (б,- + — TT7^)]} =

= Nj+i |vi+i exp К і (іі+1 — ~ Nj+1Zj) —

— xJjj+i exp [t (6j+1 + ~Nj+lZj} } . (1.4)

На то-й границе i(Vi-i = 0.

Решение позволяет однозначно определить электрическое и магнитное поля в любой точке многослойной системы с точностью до произвольной комплексной постоянной.

Поскольку в оптике многослойных оптических систем имеют дело только с относительными и усредненными во времени величи­нами, временные множители можно совсем исключить, а комплекс­ную амплитуду электрического поля на т-й границе

Ym+i Є? р К С (Е? п+1 у N rnH^mj (J считать равной единице.

Введем следующие обозначения: для волны, прошедшей в /-Й слой через (/ — 1) — ю грапицу, E]lі)+ и £$■- — электрическое поле справа от (/ — 1)-й границы и слева от /-й границы соответст-

<• , ,, .. . и Ж-|(Г)

венно; для волны, отраженной в /-и слои от /-и границы, Ьц-і)+ и Е(р —электрическое поле справа от (/ — 1)-й границы и слева от /-й границы соответственно.

Тогда

= У і ехр [і (і; — NjZj) ] ;

ЕР = t; ехр [і (Лі + -х — А>;)] ;

Е(иі1)+ = уj ехр [і (lj — ~х A’jZj-i) ] ;

£(Ьі)+ = tj ехр [* (ftj + "X Nizj-i) ] *

В нашем случае для прошедшей и отраженной волн можно

написать

Ер = ЕР и Ер} = Ер тогда

Е^ = Я^ехр [ і А^;] = ЕР exp (icpj); (1.5)

£(J-1)+ = £j — exp [ — і AVi ] = E(p exp (— iqjj), (1.6)

где Ij — Zj — Zj-i, фj — комплексная фазовая толщина 7-го слоя. Теперь уравнения (1.1) и (1.2) запишутся в виде

ЕР + ЕР = ЕР + ЕР; (1.7)

Nj (ЕР — ЕР) = NM (ЕР — ЕР). (1.8)

Заменив / на (/ — 1) в уравнениях (1.7) и (1.8), с учетом соотно­шений (1.5) и (1.6) получим

г*(0 і г(г) _______ еЧО 1 Z7(r)

+ Л0*-і)—— Л0*-і)+ + £’0-і)+ї

— ^or-D — -= (E(aPr — £&V) ВД-х,

или

Ep-ir = 7a (1 + Nj/Nj-j) Ep exp (icpj) +

+ Va (1 — A’j/Nhl)EP exp (— icpj);

Д&и — = V* (1 — AVA^-i) Ep exp (i(Pj) +

+ Va (1 + Nj/Nhl) EP exp (— гф;).

Если всего m слоев, то граничные условия выглядят так:

е% = і; еР+ = о,

ИЛИ

Е*~ = г/2 (1 + Nn+1/Nm); Е$- = v2 (1 — Nn^jNrn).

Теперь можно определить амплитудный коэффициент отраже­ния для (у 1)-й границы раздела

_ (1 —Nj/Nj-!) Ер exp (tq? j) + (1 +Ni/Nhl) Е(р exp (— tify) _

(1 — f ДуД^) E<}‘J exp(iqy + (1 — N^/N^) E<p exp (_ i<p.)

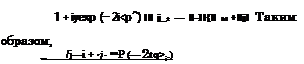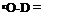
_ NjVWj-! + Nj) b rj-exp (— 2iq>j)

Аналогично получаем комплексный амплитудный коэффициент пропускания для (/ — 1)-й границы

где gj-! = 2Nj-diN)-! — f Nj).

Эту же теорию можно распространить на случай наклонного падения света [27].

Решение уравнений Максвелла для случая наклонного падения света может быть представлено в виде компактной системы урав­нений при сохранении прежних обозначений, если ввести понятия «эффективный показатель преломления» и «эффективная фазовая толщина», что позволяет получить математически корректные результаты.

В простейшем случае наклонного падения света на границу раздела двух сред легко видеть, что поперечное сечение у пре­ломленного пучка отличается от сечения падающего пучка, а у отраженного пучка не изменяется. Очевидно, в этом случае определение коэффициентов отражения и пропускания через век­тор Пойнтинга не согласуется с законом сохранения энергии, поскольку сумма этих коэффициентов будет отлична от единицы (100%). Эта несогласованность устраняется, если определить коэффициенты отражения R и пропускания Т через нормальную компоненту вектора Пойнтинга для каждого из лучей, т. е. через

световой поток, отнесенный к единице площади. Нормальные компоненты вектора Пойнтинга удобно выразить через танген­циальные компоненты векторов электрического и магнитного полей. При наклонном падении света необходимо учитывать также направление колебаний векторов поля. При этом представ­ляют интерес только два независимых направления, поскольку все остальные в силу принципа суперпозиции можно представить как линейную комбинацию этих двух. Будем рассматривать s-поляризацию, когда вектор электрического поля колеблется в плоскости, перпендикулярной плоскости падения, и р-поляри — зацию, когда вектор электрического поля колеблется в плоскости падения, т. е. в плоскости (у, z).

Пусть угол падения равен Хо — Тогда выражения для тангенци­альных компонент полей в любой точке /-го слоя по форме совпада­ют с уравнениями (1.1) и (1.2), если

а) опустить множители, описывающие зависимость от у, кото­рые в данном рассмотрении не нужны;

б) заменить Nj в экспоненциальных членах па NjCos%j, где

где

в) заменить Nj перед фигурной скобкой в уравнении (1.2) на —N j/cost j, если р-поляризация, или на N jcosxj, если s-поляризация.

Условия непрерывности на границах раздела не изменяются. Вводится эффективное значение фазовой толщины /-го слоя, равное q>jCos%j для обеих поляризаций.

1.2.

Направленное изменение оптических свойств поверхности твер­дых тел с целью получения необходимой селективности в широком интервале спектра достигается, как правило, путем оптимального сочетания характеристик подстилающей поверхности и многослой­ного покрытия.

Эта задача близка к проблеме просветления оптики, подробно освещенной в ряде фундаментальных работ [21—281. Однако про­светление оптики ограничивается в основном видимой (0,4— 0,75 мкм) частью спектра и использованием, следовательно, толь­ко тонких диэлектрических пленок интерференционной толщины, прозрачных в той области спектра, где необходимо получить эф­фект просветления (в последнее время большое внимание уделя­ется и просветлению оптических материалов для инфракрасной оптики [25, 28, 29]).

Многослойное селективное покрытие для преобразователей солнечной энергии может состоять как из набора прозрачных диэлектрических слоев строго определенной толщины (напри­мер, кратной U4), так и включать в себя частично поглощающие слои, а также слои произвольной, в том числе неинтерференцион­ной, толщины. Необходимость использования столь сложных по структуре многослойных покрытий вызвана тем, что с помощью селективного покрытия требуется получить строго определенное сочетание оптических характеристик в очень широком интервале спектра (например, от 0,2 до 30 мкм).

В настоящей главе показаны в общем виде выводы теории тон­ких интерференционных пленок как для полностью прозрачных, так и для частично поглощающих слоев, а кроме этого, приведены примеры расчета более сложных систем, включающих слои с про­извольной неинтерференционной толщиной. Каждый из примеров будет иллюстрироваться результатами расчетов селективных по­верхностей и покрытий применительно к конкретному преобра­зователю солнечной энергии.

1.1.

К полезному использованию солнечной энергии привлечено в на­стоящее время внимание большого числа исследователей во всем мире. Весьма заманчивым является экологически чистое превраще­ние в электричество и тепло энергии солнечных лучей, и вполне обоснованно, что на солнечную энергетику возлагаются сейчас большие надежды [1—5]. Резко возрос интерес как к теоретическим, так и к прикладным разработкам в области преобразователей солнечного излучения.

Всесторонне исследуются как фотохимические и биологиче­ские (диссоциация воды на водород и кислород, ускоренное про­изводство органического топлива за счет фотосинтеза и др.), так и физические (с помощью полупроводников, тепловых машин и т. д.) способы использования солнечной энергии, причем послед­ние в настоящее время в несколько раз (а то и в десятки раз) эффективнее.

Среди физических способов [61 преобразования солнечного излучения в другие виды энергии можно выделить несколько наи­более перспективных: теплоэнергетический [7], в котором исполь­зуется трехступенчатая система концентратор солнечного излуче­ния — высокотемпературный теплоприемник — тепловая машина, термоэлектрический 18], термоэмиссионный [9] и фотоэлектриче­ский [10].

Разработка теплоэнергетического метода преобразования, ис­пользующего хорошо известные в теплоэнергетике узлы, такие, как тепловые машины, была начата еще в прошлом веке. В 1878 г. на Всемирной выставке в Париже от концентратора с паровым кот­лом, установленным в его фокусе, работал печатный станок, вы­пускавший в час 500 экз. газеты «Солнце». В 50-х годах нашего столетия в СССР [11] и в 70-х годах в США [12] и Японии [13] выполнено несколько проектов больших солнечных электростан­ций с центральным котлом, установленным на высокой башне. Считается вполне реальным, что теплоэнергетический способ позволит преобразовывать солнечную энергию в электрическую с КПД, превышающим 20%.

Столь же высоких результатов удалось достичь в последнее время на практике в фотоэлектрическом методе преобразования 114]. Тем самым открываются возможности широко использовать

на Земле полупроводниковые солнечные батареи, которые в те­чение вот уже почти 20 лет, начиная с 1958 г. [15J, служили на­дежным источником электроэнергии на борту космических аппа­ратов. Солнечные батареи еще сравнительно дороги, однако соз­дание матричных фотопреобразователей, способных эффективно преобразовывать солнечное излучение сверхвысокой плотности [16], открывает возможность резкого снижения стоимости получа­емой электроэнергии за счет использования дешевых концентра­торов.

Преобразователи солнечной энергии, основанные на различных физических принципах, имеют три оптические поверхности: отражающую поверхность концентратора, приемную поверхность фото — или термопреобразователя и теплоизлучающую поверхность радиатора-охладителя. Тепловой баланс каждой из этих поверх­ностей сложен и многообразен даже в том случае, когда преобра­зователь солнечной энергии работает в условиях исключительно радиационного теплообмена (например, в космосе или в вакууми — рованной оболочке на Земле). Оптические поверхности преобра­зователей солнечной энергии являются приемником и источником теплового излучения в далеких друг от друга областях спектра. Это обстоятельство, усложняющее тепловые расчеты, позволяет в то же время влиять одновременно как на тепловоспринимающие, так и на теплоизлучающие свойства поверхностей, значительно изме­няя их, причем зачастую в противоположном направлении. Иными словами, появляется возможность управлять характери­стиками оптических поверхностей путем придания им селективных (резко отличных в соседних спектральных интервалах) оптиче­ских свойств и повышать тем самым КПД преобразователей сол­нечной энергии. Для достижения этой цели могут быть использо­ваны как механическая обработка поверхности (например, созда­нием микрорельефа определенной геометрической формы), так и нанесение однослойных и многослойных селективных оптических покрытий [17].

Селективные оптические покрытия позволяют изменять тепло­вой баланс поверхностей и аппаратов (особенно в космосе в усло­виях исключительно радиационного теплообмена), защищать полупроводниковые приборы от воздействия корпускулярной радиации, получать практически любое распределение коэффи­циента отражения от оптической поверхности, добиваться про­светления, т. е. уменьшения отражения без поглощения света самим покрытием, в области спектральной чувствительности полу­проводниковых и оптических приборов. В наиболее сложных слу­чаях, например при работе солнечных батарей в космосе, селек­тивные оптические покрытия должны решать все перечисленные выше задачи одновременно. Сложной проблемой является получе­ние покрытий, обладающих не только необходимыми оптическими характеристиками, но и полностью сохраняющих их при длитель­ной эксплуатации в космических или земных условиях, в связи с чем свойства селективных покрытий и поверхностей должны очень слабо изменяться при длительном воздействии ультрафио­летового излучения Солнца, корпускулярного облучения, микро — метеоритных потоков, глубокого вакуума, повышенной влажности и резкого термоциклирования в вакууме или па воздухе.

В результате исследований, выполненных в разных странах мира в основном в последнее десятилетие, для каждого типа пре­образователей солнечной энергии удалось создать покрытия, близкие по свойствам к оптимальным и отличающиеся высокой стабильностью.

Как будет показано в книге, селективные покрытия позволяют сохранить в теплоприемнике до 90% энергии падающего солнеч­ного излучения, почти на 50% повысить КПД фотогенераторов, в десятки и сотни раз увеличить срок активного существования солнечных батарей в радиационных поясах Земли.

Разработанные селективные поверхности и покрытия находят широкое применение не только в области преобразования сол­нечной энергии, ной в полупроводниковых источниках и прием­никах когерентного излучения [181, радиаторах космических аппаратов [19], детекторах ядерных частиц [20] и во многих дру­гих областях современной техники.

Можно с уверенностью сказать, что теоретическое обоснование и разработка селективных оптических поверхностей и покрытий представляют новое направление в области преобразования энер­гии, имеющее большое научное и практическое значение.

В природе нет поверхностей, оптические свойства которых были бы неселективными в очень широком диапазоне спектра. Все поверхности в той или иной степени селективны. Окраска окружа­ющих предметов — один из наиболее заметных примеров природ­ной еелективности. Поглощая часть лучей из видимого участка спектра, поверхность тел или покрывающая ее краска отражает остальную часть излучения, определяющую цвет поверхности. Во многих случаях поверхность, которая кажется нашему глазу неселективной — белой, черной пли серой,— резко изменяет свои свойства при переходе к инфракрасному или ультрафиолетовому интервалу спектра.

Как правило, селективность оптических свойств поверхности функциональна — она направлена на полезное изменение тепло­вого баланса тела или на помощь фотохимическим или биологи­ческим процессам внутри природного объекта. В природе были обнаружены случаи «автоматического» регулирования селектив­ных свойств поверхности. Так, измерения оптических свойств листьев некоторых пород деревьев в зависимости от окружающих температурных условий показали, что в холодную погоду листья начинают сильнее поглощать инфракрасное солнечное излучение, в то время как в жаркие месяцы в этой области спектра увеличи­вается отражение, позволяя уменьшить испарение влаги с поверх­ности листьев.

Бесконечное разнообразие природных и искусственных селек­тивных поверхностей (как с неизменными, так и с изменяющимися иод действием внешних условий оптическими свойствами) не по­зволило назвать эту книгу просто и лаконично: «Селективные поверхности». Подобное название обязывало бы рассмотреть хотя бы кратко столь обширный круг явлений, что это не удалось бы сделать на страницах одной книги.

Книга посвящена селективным поверхностям, используемым в одном из наиболее актуальных направлений современной тех­ники — при создании преобразователей энергии солнечного излу­чения, на которые в недалеком будущем будет возложена задача получения значительной части необходимой человечеству тепловой и электрической энергии, и является первой монографией в этой области.

Преобразователи солнечной энергии работают в условиях постоянного взаимодействия нескольких лучистых потоков: прямого и рассеянного солнечного излучения; солнечного излуче­ния, зеркально отраженного концентраторами; собственного теп­лового излучения рабочей и темновой поверхностей самих пре­образователей солнечного излучения; тепловых потоков, переизлу — чаемых поверхностями теплосброса (радиаторами) и прозрачной тепловой изоляции. Селективные поверхности с оптимальными оптическими характеристиками позволяют изменить тепловой баланс преобразователя в необходимом направлении и суще­ственно увеличить эффективность преобразования энергии сол­нечного излучения в тепловую и электрическую.

Основная цель настоящей монографии состояла в том, чтобы показать, как могут быть созданы оптические поверхности с се­лективными свойствами. Автор не ограничился обзором и анали­зом свойств разнообразных оптических поверхностей, применя­емых в солнечной энергетике. В монографии показаны пути на­правленного изменения оптических характеристик поверхностей, способы придания им селективных свойств, позволяющих макси­мально увеличить КПД и улучшить стабильность параметров разнообразных типов преобразователей солнечной энергии. Рас­смотрены все этапы создания селективных поверхностей — от теоретической оптимизации, указывающей предельные возмож­ности любого из применяемых методов, до результатов эксперимен­та и практического использования.

Теоретическая оптимизация и основные методики расчета приводятся в главе 1. В главе 2 рассмотрены оптические селектив­ные поверхности преобразователей солнечной энергии в электричес­кую, причем основное внимание уделено полупроводниковым фото­электрическим преобразователям, позволившим обеспечить многолет­нюю бесперебойную работу космических аппаратов. В главе 3 пока­заны пути получения селективных поверхностей для преобразовате­лей энергии солнечного излучения в тепловую, таких, например, как коллекторы «солнечных домов», обеспечивающие отопление и кондиционирование домов энергией Солнца. В главе 4 монографии рассмотрены оптические поверхности комбинированных преобразо­вателей энергии солнечного излучения одновременно в тепловую и электрическую. Эти преобразователи обладают наиболее высоким суммарным КПД, и перспективы их широкого приме­нения в ближайшем будущем несомненны.

Автор выражает искреннюю признательность за помощь в под­готовке книги В. II. Матвееву, И. П. Гавриловой, М. В. Татарен — ковой, Ю. Ы. Ксендзацкой и пользуется возможностью поблаго­дарить сотрудников, студентов, аспирантов, коллег за творческое участие в исследованиях и ответственного редактора — за внима­тельное и благожелательное отношение к этой монографии.