Определение коэффициентов отражения, пропускания и погло­щения многослойной системы с точки зрения электромагнитной теории сводится к решению граничной задачи, т. е. к определе­нию стационарных амплитуд векторов напряженности электриче­ского и магнитного полей на всех границах многослойной системы при падении световой волны с определенными характеристиками. Все энергетические соотношения и фазовые изменения выража­ются через векторы поля [27].

Будем рассматривать случай нормального падения света и выведем для него основные соотношения. Затем с помощью вве­дения соответствующих обозначений и определений эту форму решения сделаем пригодной и для расчета наклонного падения.

Допущения: 1) падающий свет описывается линейно-поляри­зованной монохроматической плоской волной; 2) ширина пучка много больше длины волны.

Первое допущение не ограничивает общности задачи. Второе же допущение о ширине луча исключает дифракционные эффекты.

Оптические свойства каждого слоя полностью описываются комплексным показателем преломления Nj = n;- — ikj (у = 1, 2, З, . . ., ш + 1) и геометрической толщиной lj. Величина kj может быть равна нулю, если в слое пет поглощения.

Внутри многослойной системы возникают интерференционные эффекты вследствие существования отраженной и прошедшей волн в каждом слое, за исключением последней, полубесконечной среды (в том числе полностью поглощающей в данной области спектра), где существует только прошедшая волна. Последнее обстоятель­ство обеспечивает граничное условие для решения уравнений Максвелла в (т + 1)-й среде.

Можно показать, что в случае нормального падения векторы электрического и магнитного полей для всех волн в каждом слое перпендикулярны друг другу и направлению распространения и, кроме того, волны однородны. Последнее означает, что электри­ческое и магнитное поля имеют только компоненты, параллельные границам раздела, и что плоскости постоянной амплитуды и пло­скости постоянной фазы в любом поглощающем слое совпадают.

Решение уравнений Максвелла для электрического и магнит­ного полей в у-м слое запишется в виде

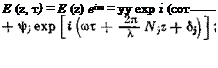(1.1)

Я (Z, т) = я (z) eimT = Nj |vj exp [i (cot——— NjZ + j —

-^exp [г (cor+ b yvjz + 6j) ]} , (1.2)

где t время; z — координата в направлении распространения излучения; у}, г|)у, £г, 6— постоянные, которые выбираются из условий непрерывности Е (г) и Н (z) на каждой границе раз­дела.

Это означает, что

У і ехР [* — -1ГNizi) ] + Ф) ехР [ ■1 («і + — Т — NjZj) ] =

= Tj+i ехР (іл-i———————— 5T~^+lZj)]

+ tj+iexp [і (б;Ч1 + -^L^j+1z/)] ; (1.3)

Nj |vjexp [і fa — -^LyVjZ,-)] — ifcexp [і (б,- + — TT7^)]} =

= Nj+i |vi+i exp К і (іі+1 — ~ Nj+1Zj) —

— xJjj+i exp [t (6j+1 + ~Nj+lZj} } . (1.4)

На то-й границе i(Vi-i = 0.

Решение позволяет однозначно определить электрическое и магнитное поля в любой точке многослойной системы с точностью до произвольной комплексной постоянной.

Поскольку в оптике многослойных оптических систем имеют дело только с относительными и усредненными во времени величи­нами, временные множители можно совсем исключить, а комплекс­ную амплитуду электрического поля на т-й границе

Ym+i Є? р К С (Е? п+1 у N rnH^mj (J считать равной единице.

Введем следующие обозначения: для волны, прошедшей в /-Й слой через (/ — 1) — ю грапицу, E]lі)+ и £$■- — электрическое поле справа от (/ — 1)-й границы и слева от /-й границы соответст-

<• , ,, .. . и Ж-|(Г)

венно; для волны, отраженной в /-и слои от /-и границы, Ьц-і)+ и Е(р —электрическое поле справа от (/ — 1)-й границы и слева от /-й границы соответственно.

Тогда

= У і ехр [і (і; — NjZj) ] ;

ЕР = t; ехр [і (Лі + -х — А>;)] ;

Е(иі1)+ = уj ехр [і (lj — ~х A’jZj-i) ] ;

£(Ьі)+ = tj ехр [* (ftj + "X Nizj-i) ] *

В нашем случае для прошедшей и отраженной волн можно

написать

Ер = ЕР и Ер} = Ер тогда

Е^ = Я^ехр [ і А^;] = ЕР exp (icpj); (1.5)

£(J-1)+ = £j — exp [ — і AVi ] = E(p exp (— iqjj), (1.6)

где Ij — Zj — Zj-i, фj — комплексная фазовая толщина 7-го слоя. Теперь уравнения (1.1) и (1.2) запишутся в виде

ЕР + ЕР = ЕР + ЕР; (1.7)

Nj (ЕР — ЕР) = NM (ЕР — ЕР). (1.8)

Заменив / на (/ — 1) в уравнениях (1.7) и (1.8), с учетом соотно­шений (1.5) и (1.6) получим

г*(0 і г(г) _______ еЧО 1 Z7(r)

+ Л0*-і)—— Л0*-і)+ + £’0-і)+ї

— ^or-D — -= (E(aPr — £&V) ВД-х,

или

Ep-ir = 7a (1 + Nj/Nj-j) Ep exp (icpj) +

+ Va (1 — A’j/Nhl)EP exp (— icpj);

Д&и — = V* (1 — AVA^-i) Ep exp (i(Pj) +

+ Va (1 + Nj/Nhl) EP exp (— гф;).

Если всего m слоев, то граничные условия выглядят так:

е% = і; еР+ = о,

ИЛИ

Е*~ = г/2 (1 + Nn+1/Nm); Е$- = v2 (1 — Nn^jNrn).

Теперь можно определить амплитудный коэффициент отраже­ния для (у 1)-й границы раздела

_ (1 —Nj/Nj-!) Ер exp (tq? j) + (1 +Ni/Nhl) Е(р exp (— tify) _

(1 — f ДуД^) E<}‘J exp(iqy + (1 — N^/N^) E<p exp (_ i<p.)

где /і_! = —5’~[1]- jV^

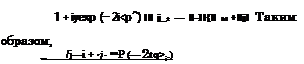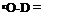
_ NjVWj-! + Nj) b rj-exp (— 2iq>j)

Аналогично получаем комплексный амплитудный коэффициент пропускания для (/ — 1)-й границы

где gj-! = 2Nj-diN)-! — f Nj).

Эту же теорию можно распространить на случай наклонного падения света [27].

Решение уравнений Максвелла для случая наклонного падения света может быть представлено в виде компактной системы урав­нений при сохранении прежних обозначений, если ввести понятия «эффективный показатель преломления» и «эффективная фазовая толщина», что позволяет получить математически корректные результаты.

В простейшем случае наклонного падения света на границу раздела двух сред легко видеть, что поперечное сечение у пре­ломленного пучка отличается от сечения падающего пучка, а у отраженного пучка не изменяется. Очевидно, в этом случае определение коэффициентов отражения и пропускания через век­тор Пойнтинга не согласуется с законом сохранения энергии, поскольку сумма этих коэффициентов будет отлична от единицы (100%). Эта несогласованность устраняется, если определить коэффициенты отражения R и пропускания Т через нормальную компоненту вектора Пойнтинга для каждого из лучей, т. е. через

световой поток, отнесенный к единице площади. Нормальные компоненты вектора Пойнтинга удобно выразить через танген­циальные компоненты векторов электрического и магнитного полей. При наклонном падении света необходимо учитывать также направление колебаний векторов поля. При этом представ­ляют интерес только два независимых направления, поскольку все остальные в силу принципа суперпозиции можно представить как линейную комбинацию этих двух. Будем рассматривать s-поляризацию, когда вектор электрического поля колеблется в плоскости, перпендикулярной плоскости падения, и р-поляри — зацию, когда вектор электрического поля колеблется в плоскости падения, т. е. в плоскости (у, z).

Пусть угол падения равен Хо — Тогда выражения для тангенци­альных компонент полей в любой точке /-го слоя по форме совпада­ют с уравнениями (1.1) и (1.2), если

а) опустить множители, описывающие зависимость от у, кото­рые в данном рассмотрении не нужны;

б) заменить Nj в экспоненциальных членах па NjCos%j, где

где

в) заменить Nj перед фигурной скобкой в уравнении (1.2) на —N j/cost j, если р-поляризация, или на N jcosxj, если s-поляризация.

Условия непрерывности на границах раздела не изменяются. Вводится эффективное значение фазовой толщины /-го слоя, равное q>jCos%j для обеих поляризаций.

1.2.