Расчет проведен для трубы с внутренними диаметрами 150 мм и 130 мм, что позволяет получать заготовки для СЭ размером 100 х 100 мм. При этом установка с трубой диаметром 150 мм работает на пределе своих возможностей со скоростью 1 мм/мин без регулиро­вания солнечного потока с помощью поворотных экранов.

Установка с кварцевой трубой диаметром 130 мм работает от концентратора диаметром 10 м в нормальном режиме с возможно­стью регулирования светового потока.

Производительность установки с трубой диаметром 130 мм составляет 52,7 — 56,7 кг/сутки.

Такая производительность (при 6-часовом режиме работы) обеспечит экономию электроэнергии на уровне

W3 = 52,7 х 120 = 6324 кВт-ч/за 6 часов.

Выводы по главе 1

Предложен и разработан метод центробежной отливки полимерных параболоидных концентраторов на подслое из кремнийорганических каучу­ков. Исследованы технологические операции метода с целью определения и прогнозирования точности получаемых концентраторов.

По данному методу изготовлены концентраторы в виде гальваноко­пий из никеля и меди диаметрами от 1,5 до 2,5 м, причём концентратор 0 2,5 м выполнен в виде секторных отражателей.

Разработана методика оптических испытаний солнечных параболо­идных концентраторов на аберрографе Леонова.

Предложена матрица с перенастраиваемой поверхностью для мол­нирования параболоидных поверхностей крупных размеров. Матрица ис­пользована для изготовления концентратора 010 м для солнечной высоко­температурной установки ВТСУ-10 в г. Ереване.

Рассмотрена возможность использования параболоидного концен­тратора 0 10 м для выращивания монокристалла кремния, проведен оце­ночный расчёт, показавший возможность выращивать монокристаллы диа­метром до 130 мм.

КОНЦЕНТРАТОРЫ НА ОСНОВЕ КОНЦЕНТРИЧЕСКИХ

На рис. 1.28 изображена зона плавки в кварцевой трубе. В кварцевой трубе 1 находится материал заготовки 2, который вместе с трубой движется вверх со скоростью V, проходя зону Н, где мате­риал облучается интенсивным световым потоком и расплавляется.

Твердый кристалл 3 формируется на границе фазового пере­хода Ф (фронт кристаллизации). Диаметр кристалла 3 меньше внут­реннего диаметра кварцевой трубы, в зазоре 4 поддерживается ваку­ум. Поэтому в тепловых расчётах принято, что вверх от границы Ф теплоотвод от кристалла происходит только излучением и тепло­проводностью вдоль оси кристалла. Ниже границы Ф теплоотвод происходит излучением, теплопроводностью и конвекцией.

Процесс выращивания монокристалла состоит в следующем.

Затравка 3, вытягивающая из расплава кристалл, вытягивает кристалл со скоростью V относительно неподвижного фокуса F, при этом труба и затравка вращаются в разные стороны. Плоскость А-А является границей раздела чисто жидкой фазы расплава и зоны пе­реходных процессов к фронту кристаллизации Ф. За счёт поверхно­стных сил натяжения создаются радиусы зоны и зазор 4 между кри­сталлом и трубой. На рис. 1.28 указана зона Z, в пределах которой температура падает до температуры окружающей среды, зона Z’, в которой температура опускается от температуры плавки до темпера­туры заготовки [1.23,1.24].

Для рассматриваемого процесса приняты следующие допуще­ния: фронты кристаллизации и плавления приняты плоскими; за­травка и выращиваемый кристалл рассматриваются как единое це­лое; теплофизические параметры не зависят от времени; распреде­ление плотности солнечного излучения по поверхности зоны Н при­нимается равномерным; изменение температур по зонам Z и Z’ яв­ляется линейным; расчетный диаметр кристалла равен внутреннему диаметру трубы ( погрешность не более 6%); в жидком расплаве зо­ны Н нет градиента температур по оси Z; конвективные потери имеют место с зоны Z +Н; теплофизические параметры заготовки принимаются близкими к параметрам кристаллического кремния,

ПОЭТОМУ Z’= Z, Q£ Z’ = Qe Zj Ql = Q’l-

Уравнение баланса энергии процесса может быть записано в следующем виде:

Qo + Ql — Qc — Q’l — QeH — Qe Z — Qe Z’ — Qa = 0> (1-13)

где Qo — энергия, поступающая от солнечного излучения; QL — энер­гия, поступающая за счёт скрытой теплоты кристаллизации; Qc — энергия на разогрев исходного материала до температуры плавле­ния; Q’l — энергия на расплав материала (изменение фазового со­стояния); QeH — потери энергии путём излучения в зоне Н; Qe z — по­тери на излучение в зоне роста кристалла Z при средней температу­ре Т ; Qe г ~ потери на излучение в зоне заготовки при средней тем­пературе Т на размере Z’; Qa — конвективные потери на размере Z’ + Н.

Запишем уравнения для каждого составляющего в (1.13).

Поступление солнечной энергии

Qo= E0S3®Tiz. (1.14)

Энергия плавления или кристаллизации:

Ql = Q’l = pLSkpV, (1.15)

где р — плотность кремния (2,33 г/см2); L — скрытая теплота плавле­ния (кристаллизации); S,<p — поперечное сечение кристалла

(Бкр = яг2).

Теплота разогрева материала заготовки:

Qc=CSKpVp(TH-T0), (1.16)

где С — теплоёмкость материала заготовки; Тн — температура рас­плава в зоне Н, которую рекомендуется принимать выше, чем тем­пература плавления кремния (1420 °С), Тн = 1723°К.

Потери тепла на излучение в зоне Н:

QEH=asH(T^-T04)SKpH, (1.17)

где а — постоянная Стефана-Больцмана; єн — излучательная способ­ность кремния, т. к. Т0 « Тн, в дальнейшем Т0 пренебрегаем.

Потери тепла излучением в зонах Z и Z:

Qez = QeZ — = cje2(f)4SKpZ, (1.18)

где ez — излучательная способность кристалла и материала заготовки

при средней температуре Г в пределах зон Z и ZТ = 0,5 (Тн + Т0).

Потери тепла на свободную конвекцию:

Qa = a(f-T0)STp(H+Z’), (L19)

где а коэффициент теплоотдачи при свободной конвекции для воз­духа при температуре Т.

Основным фактором, влияющим на процесс кристаллизации, является рассеяние теплоты кристаллизации путем излучения с по­верхности кристалла на размере Z. Поэтому оптимизация процесса плавки в солнечной печи может быть проведена путем рассмотрения двух процессов, разделенных фронтом кристаллизации Ф: процесс роста кристалла выше зоны Ф и отвод выделяющейся при этом теп­лоты путём теплопроводности по кристаллу и излучением, и про­цесс ниже зоны фронта Ф, обеспечиваемый солнечной энергией. В таком случае процесс роста кристалла может быть рассмотрен в тра­диционной постановке задачи для процесса Чохральского [1.23, 1.24], и определена максимальная скорость роста кристаллизации

Vmax При УСЛОВИИ

Qa = QeZ — (1.20)

Определение скорости роста кристалла. Количество тепло­ты, выделяющейся при кристаллизации и отводимой через кристалл в единицу времени:

d Ql = р L SKp dZ/dx. (1.21)

Поскольку теплота d QL отводится с границы фронта кристал­лизации путём теплопроводности, можно записать:

р L SKp dZ/dt = S. pA. HdT/dZ,

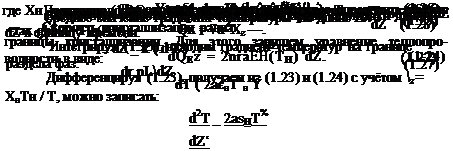
Реальные скорости роста обычно ниже V,^ и находятся в пределах 1-2 мм/мин.

Определение теплопотерь через конвекцию. Коэффициент теплоотдачи а определяем для вертикальной трубы в обширном пространстве воздуха для наружной стенки, при этом пренебрегаем теплопотерями по толщине стенки (5 мм); принимаем среднюю тем­пературу по длине Z одинаковой; принимаем, что режим переноса воздуха по всему размеру Z одинаков.

Критерий Нуссельта:

«Z

Nu = — = k(Cr Рг)" m, (1.29)

К

где Я, в — теплопроводность воздуха; СгРг — критерии Грасгофа и Прандтля; k, n, m — коэффициенты: к = 0,8, п = 0,25, m = = 1+(1+1/Рг0’5)2 для СгРг = 103 — 104; к = 0,15, п = 0,33, m = 1, для СгРг > 109 (турбулентный режим).

Критерий Грасгофа:

Cr = gp(f-T0)(H + Z)3/v2B, (1.30)

где g — ускорение свободного падения; р — коэффициент объемного расширения воздуха; v — кинематическая вязкость воздуха. Критерий Прандтля:

Рг = v / а,

где а — коэффициент температуропроводности воздуха.

Отсюда следует:

Nuljj

Z + H

Плотность облучения в зоне плавления. Плотность облуче­ния зоны Н определяем по формуле:

qH=Qo/2TtrH. (1.32)

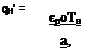Плотность излучения, необходимую для достижения темпера­туры плавления кремния Тн = 1723°С, определяем по формуле:

где as — коэффициент поглощения кремния при температуре Тн.

Для правильно выбранных параметров процесса qH> Цн-

Производительность процесса. Количество кремния, выра­щенного в 1 час при коэффициенте полезного использования време­ни 0,75, составит:

P^pSKpV.^0,75. (1.34)

Суточная производительность при длительности среднего светового дня 6 часов составит Рс= 6 Р.

На рис. 1.26 приведена схема ВТСУ для зонной плавки моно­кристаллов кремния.

Параболоидный концентратор 1 диаметром 10 м установлен на несущей ферме 2. Отражающая поверхность выполнена в виде параболоидных фацет 3 с механизмами юстировки 4. Поворотные шторы 8, расположенные по периферии концентратора предназна­чены для частичного регулирования светового потока на концентра­тор для поддержания необходимого теплового режима в зоне плав­ки. Механизм вращения кварцевой трубы 6, в которой находится исходный материал плавки, удерживается трубой 7 с механизмом вращения 5. Неподвижное плоское зеркало 9, установленное на раме 10, направляет световой поток от гелиостата 11 вертикально, парал­лельно главной оптической оси концентратора. Гелиостат 11 для уменьшения размеров выполнен на поворотной платформе с воз­можностью вращения вокруг оси 13. Гелиостат следит за положени­ем Солнца на небосводе и поддерживает постоянным направление светового потока на концентратор. Концентратор собирает солнеч­ное излучение в фокусе F.

Геометрические параметры концентратора: диаметр 10 м, фокусное расстояние 4,329 м, угол на сторону 60°, глубина параболы 1,443 м.

Светопропускание оптической системы. Общее светопро — пускание (r|s) определяется следующим выражением:

ТІХ= Лі Х Т|2 X Лз Х "П4 Х ТІ5 ,

где т|!, т|2, т|з — коэффициенты отражения подвижного гелиостата, неподвижного зеркала и концентратора; г|4 — коэффициент светопо- терь от френелевского отражения для потока, отраженного от кон­центратора при входе в кварцевую трубу; ц5- потери на поглощение в кварцевом стекле трубы.

Коэффициент френелевских потерь определяется с учётом прихода лучей от разных кольцевых зон концентратора под разными углами:

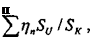
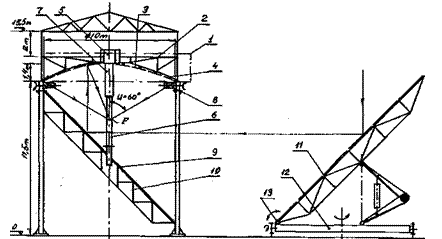(1.9)

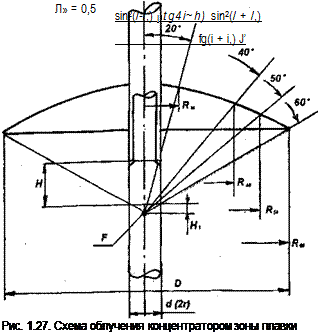
где г|п — френелевское отражение кольцевой зоны п с граничными углами раскрытия U, показанными на рис. 1.27.

і’

где і, /‘і — углы падения и преломления лучей на поверхности кварце­вой трубы.

На рис. 1.27 показаны зоны с граничными углами раскрытия от 20° до 60° с интервалом в 20° и соответствующие им радиусы концентратора. В таблице 1.2 приведены параметры расчёта френе­левского светопропускания.

При больших углах падения лучей на кварцевую трубу (зона с углами 20°) эффективность низка, поэтому эффективная площадь концентратора принята S^= Sk — S2o= 71,2 м2.

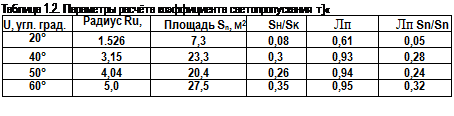
Примечания. Коэффициент преломления принят 1,5.

Полная площадь концентратора 78,5 м2.

Потери на поглощение света в кварцевой трубе г|5 подсчиты­ваем по формуле:

т|5 = (r|nor)L, где Т1пог= 0,98 — поглощение кварца на длине 1 см;

L = 0,5 см — толщина кварцевой трубы (ті5 = 0,98°’5 = 0.989). Суммарное светопропускание т|£ составит величину при ко­эффициенте отражения от одного зеркального покрытия т|j= г|2= т|з= = 0,87 (с учётом всех потерь):

Лі=0,873 х 0,989 = 0,65. (1.11)

Поворот световых экранов (рис. 1.26, поз.8), установленных между R5o и Rso, дает возможность регулировать световой поток в пределах 10% от всего приходящего потока.

Зона плавки (Н) определяется из следующих соображений (рис. 1.27): верхняя граница определяется от зоны R20, нижняя — от зоны Rfi0. Высота зоны Н определяется по формуле

^соз2(Л ( cos 60 ^

sin20

где Rbh — внутренний радиус кварцевой трубы.

Размер РІ! от зоны Н до расчётного фокуса F: Hi = Rbh cos 60/ sin 60.

Вопросы прямого технологического использования параболо­идных концентраторов продолжают оставаться в поле зрения иссле­дователей. Высокотемпературная солнечная установка (ВТСУ), по­добная созданной в г. Ереване с вертикальной оптической осью, под­ходит для процесса выращивания монокристаллов кремния методом безтиглевой зонной плавкой. Солнечный процесс выращивания мо­нокристаллов кремния при соответствующих климатических усло­виях может дать существенную экономию электроэнергии, т. к. для такого процесса для выращивания 1 кг монокристалла требуется энергия около 120 кВт-ч.

Солнечная печь (рис. 1.23, а) с вертикальной оптической осью была построена в г. Ереване. Схема её представлена на рис. 1.23, б. Установка предназнача­лась для проведения вы­сокотемпературных ис­следований различных материалов в фокусе кон­центратора диаметром 10 м, который освещался солнечным светом от ге­лиостата, расположенного

Рис. 1.23, а. Солнечная
высокотемпературная
установка (ВТСУ-10)
с концентратором, изготов-
ленным методом молниро-
вания по матрице
с перенастраиваемой
поверхностью, 010 м
(г. Ереван)

под концентратором. Отражающая поверхность была выполнена методом молирования по матрице с изменяемой поверхностью [1.14] в Армянском отделении ВНИИТ [1.15].

В г. Ташкенте была разработана и изготовлена солнечная фо­тоэлектрическая установка мощностью 1 кВт (рис. 1.24). В установ­ке [1.20] использовались параболоидные концентраторы, молниро­ванные по жесткой матрице. Модуль установки состоял из концен­тратора диаметром 0,5 м, фотоэлектрического элемента диаметром 50 мм, установленного на тепловой трубе (рис. 1.25), обеспечиваю­щей охлаждение СЭ, концентрация излучения на которых была 50. Поверхность концентратора бьша смоделирована так, что в плоско ста СЭ имела усреднённое распределение энергии. В установке бы­ло предложено много оригинальных решений в том числе: соедине­ние СЭ с металлической подложкой с помощью теплопроводного 38

слоя, не создающего напряжений на СЭ; легкое крепление тепловых труб с помощью тросовых растяжек; оригинальное решение несу­щей конструкции рамы, обеспечивающей балансировку её при вра­щении и не создающей сильных ветровых нагрузок.

1.4.3. Интенсивным методом испытаний являются солнечные натур­ные испытания концентраторов, при которых определяются: распре­деление энергии по фокальному пятну в «прицельном» положении (точное направление на Солнце в пределах отклонения порядка 1-5 угловых минут); деформация эпюры распределения при угловых и линейных дефокусировках от точки фокуса. На рис. 1.22 показан

составной концентратор диаметром 2,5 м, изготовленный методом центробежного литья и гальванопластики, подготовленный к иссле­дованию фокального пятна методом фотометрирования.

Суть метода: фокальное пятно исследуется тонким стеклян­ным световодом, один торец которого охлаждается проточной во­дой, другой вставлен в фотометричний шар, где происходит замер освещённости. Таким образом записывается кривая плотности ос­вещённости в фокальном пятне. Для того чтобы соотнести коорди­наты полученной кривой с энергетическими величинами в Вт/м2, необходимо провести тарировку полученных кривых с использова­нием калориметра [1.21].

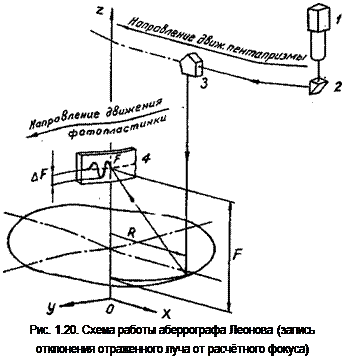
Суть метода состоит в записи отклонений от расчётного фо­куса отражённого от поверхности луча, приход которого на поверх­ность обеспечивается параллельно главной оптической оси. На рис. 1.20 показана схема аберрографа Леонова. Работает прибор сле­дующим образом: тонкий луч от коллектора 1 (можно лазерного ис­точника) попадает в пентапризму 3, откуда падает параллельно главной оптической оси OZ на отражающую поверхность концен­тратора. Отражённый луч света оставляет на фотоплёнке 4, установ­ленной в оптическом фокусе концентратора, след и вследствие пе­ремещения фотопластины происходит запись отклонения отражён­ного луча от расчётного фокуса концентратора [1.17, 1.18].

а

Метод позволяет определить продольные (вдоль оптической оси) аберрограмы концентратора при различных положениях па­дающего луча, что позволяет рассчитать действительное фокусное расстояние, определить угловые погрешности всего отражателя. По­скольку метод единичного луча является универсальным и широко применяется для исследований концентраторов разного типа и кон­струкций, то следует более подробно остановиться на определении угловых погрешностей. При обработке результатов следует учиты­вать ценность кольцевых зон отражающей поверхности, которые принимаются пропорциональными площади зоны.

Последовательность обработки полученных продольных абер­раций:

1.

Определяем средние арифметические продольные аберра­ции для каждой зоны:

(1.3)

где AFn — аберрация позиции j для зоны n; j — число снятых точек.

2. Находим действительное фокусное расстояние концентра­тора:

Х>Х

■ F-F„±-4————- , (1.4)

XX

і

где Fh — номинальное фокусное расстояние; Mj — ценность зоны площадки вокруг точки j зоны п; Мп — ценность зоны п.

3. Пересчитываем аберрации точек по отношению к действи­тельному фокусному расстоянию.

4. Подсчитываем угловые погрешности поверхности как угло­вое отклонение действительного луча от идеального направления в расчётный фокус F:

б = arctg AF/(zj + 2F),

где ДБ — действительные продольные аберрации относительно дей­ствительного фокусного расстояния; Zj — координаты точки j по оси Z (главной оптической оси концентратора).

5. Средняя квадратическая угловых погрешностей концентра­тора:

где <тп — средняя квадратическая угловая погрешность зоны п.

6. Среднюю квадратическую погрешность поперечной абер­рации Дг (по радиусу фокального пятна рассеяния) определяем по формуле:

ї>,

где Стдг — средняя квадратическая погрешность поперечной аберра­ции Аг зоны п.

Вероятность попадания отражённого луча в круг радиуса стДг равна 68%, в круг радиуса 2 аДг составляет 95%.

При необходимости по аберрограммам можно смоделировать кривую плотности излучения в фокальном пятне [1.19, 1.20]. Метод единичного луча является универсальным и широко применяется для исследований концентраторов разного типа и конструкций.

1.4.1. Качественная оценка поверхности

Суть метода состоит в том, что в фокальной плоскости пара­болоидного зеркала устанавливают светящееся изображение геомет­рических фигур, например прямоугольной сетки (сетки Чиколева), а на расстоянии 7-10 f (f — фокусное расстояние) устанавливают фо­тоаппарат и фотографируют изображение сетки. На рис. 1.19, а представлена сетка, снятая при испытаниях концентратора, изготов­ленного методом центробежного литья и гальванопластики. На рис. 1.9, б показана гальванокопия, упрочнённая с тыльной стороны пенопластмассой, что привело к значительным деформациям. Метод даёт качественную оценку отражающей поверхности, позволяет вы­явить зоны её деформации.

1.3.2. 1Метод прогиба плоских зеркал для получения концентраторов значительных размеров с высшими оптическими характеристиками впервые использовал французский исследователь Ф. Тромб при из­готовлении солнечной печи в Пиренеях. Стекло по этому методу

прогибается по опорам, расположенным по его периферии, путём приложения усилий в центре стекла, причём величина прогиба должна находиться в пределах упругого прогиба. Был предложен оптический элемент, позволяющий осуществить прогиб отражаю­щих фацет на небольших пластинах. На рис. 1.18 показан оптиче­ский элемент 1, прогиб которого по металлической подложке 2 осу­ществляет винт 5 через резиновые прокладки 8. Большое количество таких элементов, собранных на плоской панели 3, с помощью вин­тов 4 ориентируются так, что отражают солнечный поток в общий фокус [1.16].

1.3.1. Метод молнирования стекла

Метод моллирования, хорошо известный в стеклянной про­мышленности, заключается в прогибе листового стекла на металли­ческую матрицу при нагреве до температур размягчения стекла под действием силы веса или вакуума. Таким методом изготавливались прожекторные отражатели диаметром до 3 м, этим же методом изго­тавливаются отражатели строительных прожекторов диаметром до 0,5 м.

Для изготовления концентратора диаметром 10 м для высоко­температурной солнечной печи в г. Ереване [1.13] была предложена матрица для моллирования отдельных фрагментов концентратора с перенастраиваемой поверхностью [1.14]. Суть метода демонстриру­ется на рис. 1.17. Матрица состоит из плиты 1, на которой установ­лены стойки 2 с поворотными площадками 4. Перед молнированием площадки 4 устанавливаются по касательным к необходимой по­верхности 3 с помощью специальных шаблонов. Ориентированные площадки на стойках 2 фиксируются. Таким образом матрица готова к проведению процесса моллирования. При необходимости, исполь-

ц_р

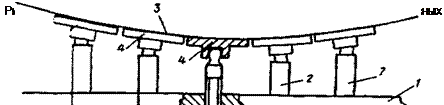
зуя другой шаблон, стойка 2 и площадки 4 могут быть перенастрое­ны на другую поверхность 3. Использование таких матриц позволи­ло изготовить концентратор диаметром 10 м [1.15].