3.1. Market analysis

The market analysis provides an in depth analysis of markets for small scale SolarCombi+ and serves as a basis for the definition of the cases to be studied in WP3. It is performed on three pillars: (i) small scale chillers, (ii) solar thermal applications and (iii) consumers. The ecologically and economically rated case studies of WP3 are on the other hand the basis for a SWOT analysis, the examination of market shares and definition of goals.

3.2. Virtual case studies

Based on the results of the market analysis and on the experience with installed systems up to now, promising configurations will be identified, simulated for different typical conditions (i. e. utiliza­tion, climate, building type) and finally economically and ecologically rated.

The data collection system receives and stores all the information generated by the temperature differential controller (RESOL, DeltaSOL ES in multiple collector orientation with multiple heat delivery points operation mode) that in turn receives this information from the temperature probes and the flow meter on the totalizing line.

This information is available and can be downloaded locally, through ports and standard communications protocols, but also remotely, via a remote communication system (GSM modem), after connection to a Data logger (RESOL DL1), which can transmit via GSM through a SIEMENS TC35i modem connected to a YAGI ASPJ 810 antenna. The data download is done by using the data logger’s specific software: RESOL Service Centre.

The data downloaded from the data logger which is important in the course of the monitoring consists in:

• 4 Temperature columns [°C]: in the feeding line leading to the collectors (cold probe), West collectors, East Collectors and Totalizing line;

• Flow [m3/h];

• Pumps operating mode [%] (always 0 or 100% for each side of the installation);

• System time;

• Amount of collected energy (cumulative) [Wh].

Every month the data downloaded is analyzed based on the following aspects and visualizations:

• Month period simple statistical analysis of the temperature probes (maximum, minimum, average and daytime average);

• Monthly radiation incident in the collectors compared with (instantaneous) extracted energy

• Monthly period temperature profile of the installation;

• Monthly plot of the extracted energy versus total incident radiation;

• Flow (monthly plot).

The COP of the heat pump was determined by:

COP = Q^ (1)

W

comp

where Wcomp is the true power input to the compressor measured directly by the wattmeter, and Qc was determined by:

Qc = mr (h2- h) (2)

Where mr is the mass flow rate of the refrigerant, and h2 and h3 are the enthalpies at the inlet and outlet of the condenser, on the refrigerant side. Enthalpy is a function of both pressure and temperature, which are measured at each point throughout the cycle.

The natural convection flow rate, mNC can be determined by performing an energy balance across the condenser. Assuming the heat lost to the environment is negligible, as the condenser was well insulated, the energy balance is expressed as:

Qc = mr (h2 — h3) = mNCCp (T8 — T7 ) (3)

where Cp is the specific heat of the water. Rearranging Eq. 3, the natural convection flow rate is then expressed as:

2. Results and Discussion

An analysis was conducted on the operation of an ISAHP with a varying temperature input. The mains water temperature, and therefore initial storage tank temperature was approximately 20°C. Figure 3 shows the power delivered to the glycol through the heaters, as well as; heat transferred to the refrigerant through the evaporator; heat rejected to the natural convection loop through the condenser; and power consumed by the compressor.

As shown in Figure 3, the heat transferred from the glycol through the evaporator exceeds the heat delivered to the glycol through the auxiliary heaters. This is due to a large amount of glycol in the auxiliary heaters which are initially at a higher temperature. The heat pump unit extracts the extra energy until the heat transferred through the evaporator matches the heat input to the glycol through the heaters. Finally, the heat transfer through the evaporator is observed to lag the heater input, again due to the volume of glycol in the auxiliary heaters.

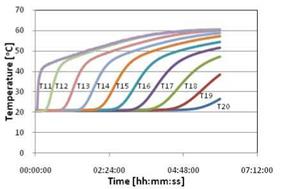
A temperature probe installed within the storage tank, with thermocouples spaced 0.15 m apart, was used to determine the level of stratification of the tank. Figure 4 shows the temperatures measured in the tank throughout the test, with T11 being the temperature measured at the top of the tank, and T20 measured at the bottom. During the test the tank was observed to stratify well, and throughout the test the temperature at the bottom of the tank, T20, remains constant at approximately 21°C. Therefore, over the course of the test, the temperature of the water entering the natural convection heat exchanger/condenser was effectively constant at 21°C.

The natural convection flow rate was also calculated over the length of the test. Figure 5 shows the natural convection flow rate of water through the condenser, plotted with the temperature of glycol delivered to the evaporator on the same graph. Consistent with the previous constant temperature tests, it was observed that higher glycol temperatures delivered to the evaporator increased the flow rate, and an increase in tank temperature decrease the flow rate. This resulted in the natural convection flow rate remaining constant for the first half of the test, and then decreasing as the glycol temperature declined, and tank temperature continued to increase.

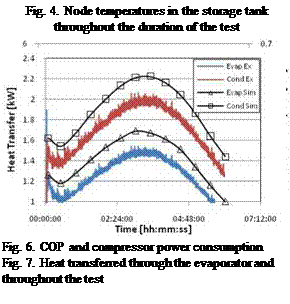
In order to compare the dynamic operation of the heat pump with the steady-state model, the measured compressor power and heat pump COP were plotted with the simulated results on the same figure. To assist in validating the computer model, the simulation was run under the same conditions as the experiment. The model predicted the power consumed by the compressor, the evaporator and condenser heat transfer rates, and the COP of the system. Figure 6 shows the heat

transfer rates through the condenser and evaporator and Figure 7 shows the COP and compressor power curves throughout the test. Both simulated and experimental values are displayed.

Fig. 5. Natural convection flow rate of water through the condenser

COP values measured throughout the test ranged from 2.4 to 3.2, and the measured compressor power ranged from 484 to 635 W. The amount of heat transferred through the condenser to the natural convection loop ranged from 1300 to 2000 kW.

Similar to the previous tests [13] run at constant glycol temperatures, the simulation program was found to overestimate the COP and heat transferred through both heat exchangers, but predicted the compressor power consumption reasonably well. Both heat transfer rates, and the COP, were over-predicted by the simulation by approximately 12%. These results were previously attributed to an over estimation of the heat exchanger effectiveness values. Neglecting this offset, the simulation, based on a steady-state governing equations, predicts the trend of the heat pump system well.

3. Future Work

Further testing is to be carried out, investigating wider ranges of temperatures and operating conditions. New heat exchanger relationships will be derived to better predict the effectiveness values, which will bring the model in to better agreement with the actual results. With the model refined, full year simulations in TRNSYS will be carried out to determine seasonal solar fraction values for the ISAHP system.

4. Conclusion

The experimental results matched well with the simulated results for the compressor power input, but the simulation over predicted the performance on the system. The compressor power input ranged from 484 — 635 W, and the COP of the system ranged from 2.4 — 3.2 over the duration of the test. The computer model predicted the dynamic operation of the system well, except for a 12% overestimation of performance due to the model’s effectiveness relationships. New seasonal solar fraction values and life cycle cost numbers will be calculated once the full year simulations are completed in TRNSYS.

3. Acknowledgments

Support for this work was provided by the Solar Buildings Research Network of Canada, the Ontario Graduate Scholarship Program, and the Natural Science and Engineering Research Council of Canada.

References

[1] NRCan, (2006). Energy Use Data Handbook, Natural Resources Canada.

[2] C. Aguilar, D. J. White, D. L. Ryan, (2005). Domestic Water Heating and Water Heater Energy Consumption in Canada, Canadian Building Energy End-Use Data and Analysis Centre

[3] G. A. Freeman, (1997). Indirect Solar-Assisted Heat Pumps for Application in the Canadian Environment, Masters Thesis, Department of Mechanical Engineering, Queen’s University.

[4] G. A. Freeman, S. J. Harrison, (1997). Solar Assisted Heat Pump Hot Water Heaters for the Canadian Environment, Proceedings of 1997 SESCI Conference, Vancouver, BC.

[5] K. Chaturvedi, J. Y. Shen, (1982). Analysis of Two-Phase Flow Solar Collectors with Application to Heat Pumps, Journal of Solar Energy Engineering, Vol. 104, 358

[6] Morrison, G. L, (1994). Simulation of Packaged Solar Heat-Pump Water Heaters, Solar Energy, Vol. 53, 249

[7] P. Sporn, E. R. Ambrose, (1955). The Heat Pump and Solar Energy, Proceedings of the World Symposium on Applied Solar Energy, Phoenix, Ariz.

[8] Chaturvedi, K., Abazeri, M, (1987). Transient Simulation of a Capacity-Modulated Direct-Expansion, Solar-Assisted Heat Pump, Journal of Solar Energy, Vol. 39, 441

[9] B. J. Huang, J. P. Chyng, (1998). Integral-Type Solar-Assisted Heat Pump Water Heater, Journal of Renewable Energy, Vol. 16, 731

[10] B. J. Huang, C. P. Lee, (2003). Long-Term Performance of Solar-Assisted Heat Pump Water Heater, Journal of Renewable Energy, Vol. 29, 633

[11] J. M. Purdy, S. J. Harrison, P.H. Oosthuizen, (1998). Compact Heat Exchanger Evaluation for Natural Convection Applications, Proceedings of the 11th IHTC Heat Transfer 1998, Korea, Vol. 6, 305

[12] University of Wisconsin, Solar Energy Laboratory, (2006). TRNSYS: A Transient Simulation Program, Madison

[13] A. Bridgeman, S. J. Harrison, (2008). Preliminary Experimental Evaluation of Indirect Solar Assisted Heat Pump Systems, Proceedings for The 3rd Annual Canadian Solar Buildings Conference, Fredericton, NB

[14] A. H. Fanney, S. A. Klein, (1988). Thermal Performance Comparisons for Solar Hot Water Systems Subjected to Various Collector Array Flow Rates, Proceedings of Intersol 85, Montreal, QC.

The typical thickness of a PUR storage insulation is in the range of 10 to 12 cm [5]. Within this study the thickness has been varied between 7.5 cm and 17.5 cm (base case 15 cm). The results of the optimisation process for these variations are shown in Figure 3 (d) and Table 1.

The optimisation with 7.5 cm of insulation leads to a system with a storage device capacity of 0.77 m3 and a solar collector area of 12 m2. Thicker storage insulation leads to an improvement of the thermal behaviour of the system. Therefore with the same dimensioning and investment cost but thicker insulation a dot in Figure 3 would shift towards higher primary energy savings and simultaneously towards smaller additional costs (due to a reduction of running costs). Thus, the optimisation curves in Figure 3 (d) shift down and flatten with an enlargement in insulation. A solely parallel movement of the curves to smaller additional costs would mean that the point of intersection of the tangent would move left, whereas a flattening of the curves would lead to a point of intersection with higher primary energy savings. Figure 3 (d) shows that the optimised

system configurations shift towards smaller primary energy savings and Table 1 indicates that the resulting dimensions are getting smaller. This means that the reduction of additional cost dominates the increasing primary energy savings. The bigger the thickness of insulation gets the smaller the distance between the resulting curves become. With an insulation thickness of 17.5 cm nearly no difference is apparent to the base case. A cross check taking into account increasing investment costs with thicker insulation showed that the results summarised in Table 1 change insignificantly.

The mobility of a solar thermal plant depends partly on tank size. The tank sizing for Case 2 (600m3) starts to be over the limit of going from factory built to site built, at least as a single tank. Up to a certain size, however, this can be arranged with 2-3 smaller tanks. Based on a telephone interview with a storage tank manufacturer this solution may also be cheaper up to 500-700 m3.

The cost of moving the panel array is unknown. Nobody has reportedly done this or documented the costs of doing it. The collector manufacturers for large arrays do not give out the information of their installation costs nor do they deliver collectors only; they sell only whole solar loop installations.

Some assumptions can be made based on a few documented projects. One german project reports [13] panel array installation costs to 60 EUR/m2 (although crane and transport not separated). Assuming the same 60 EUR/m2 for re-installation, and that dismantling and transport would be half of that, we come

to a rough estimation of 90 EUR/m2 which is about 20-25% of the initial investment. Making an estimation from the feasibility graphs for Case 1 and Case 2 this means roughly 3-6 years of prolonged payback time. It seems that with the presented feasible payback periods and current energy prices there is no room for added costs from moving the solar plant within its lifetime.

3. Conclusion

A feasibility study to find out general boundary conditions for combining solar thermal plants with small scale district heating networks under north European conditions was done. Even though the scenario was such that we connect solar to an existing plant, the conclusions made based on the results should be valid also for new plants with reasonable accuracy.

Cost breakdown:

The most costly part of the system is the collector array. The fixed costs play a smaller and smaller part in the total cost with increased system size, resulting in lower specific costs and thus improved economic viability, assuming the saved fuels are the same. The tank is the second largest investment. Other costs are relatively small compared to these, and only marginally affect the economic viability.

Pellets as fuel:

In the considered range 0.5-2 MWth, if the load is mainly space heating (Case 1) the results would imply that with todays pellet prices it will be difficult to find a feasible payback period during the plants estimated lifetime in the studied climate. Even with annual price increase rates of 5-10 % the investment seems difficult to justify economically without subsidies. For Case 2 we can find feasible payback periods shorter than the estimated lifetime of the system, but based on the studied plant portfolio, this kind of load profiles seem to be exceptions.

Oil as fuel:

If the replaced fuel is oil, then the feasible payback periods look different from the case of pellets. For Case 1 they are between 10-20 years and for Case 2 between 7-15 years depending on country and scenario.

Plant mobility:

The rough estimation made about dismantling and moving a plant implies that with current fuel prices the plant payback period is prolonged by 3-6 years. This cannot be justified regarding the feasible payback periods of the whole plant in general.

Acknowledgements

We are grateful to VAPO Oy for collaboration and financing.

References

[1] Streicher W. et al., Solarunterstutzte Warmenetze, Endbericht zum gleichnamigen Projekt in der Forschungsausschreibung „Haus der Zukunft“ im Auftrag des BMVIT, Technischen Universitat Graz (2002).

[2] Hahne E. et al., Solar unterstutzte Nahwarmeversorgung mit und ohne Langzeit-Warmespeicher „Forschungsbericht zum BMBF-Vorhaben“, Universitat Stuttgart (1998).

1st International Congress on Heating, Cooling, and Buildings — 7th to 10th October, Lisbon — Portugal /

[3] Hahne E. et al., Solar unterstutzte Nahwarmeversorgung mit und ohne Langzeit-Warmespeicher „Forschungsbericht zum BMBF-Vorhaben“, Universitat Stuttgart (2003).

[4] Muller-Steinhagen H. et al., Solar unterstutzte Nahwarmeversorgung und Langzeit-Warmespeicher „Forschungsbericht zum BMBF-Vorhaben“, Universitat Stuttgart (2005).

[5] Schmidt T., Mangold D., Status der Solaren Nahwarme in Deutschland, Universitat Stuttgart (2003 Conference presentation at „Solaren Kombianlagen fur Mehrfamilienhauser im europaischen Vergleich“).

[6] Holter C., Solarenergie & Biomasse, eine Erfolgsstory, S. O.L. I.D. Gmbh (2005 Conference presentation at „Mitteleuropaische Biomassekonferenz“).

[7] Calminder B. et al., Medelstora solvarmeanlaggningar — En utvardering av medelstora solvarmeanlaggningar utforda under perioden 1993-2000, K-Konsult Energi Stockholm AB (2002).

[8] Kovacs et al., Solenergi i industriell processvarme — En forstudie av svenska mojligheter, SP-Rapport 2003:16 (2003).

[9] Lundgren J., Hermansson R., Solar Assisted Small-Scale Biomass District Heating System in the Northern Part of Sweden, International Journal of Green Energy (2004).

[10] Dalenback J-O., Solar thermal market development in Europe, (Conference presentation at Northsun 2005).

[11] Dalenback J-O., Large-scale solar heating systems — a challenge for Europe, (Conference presentation at Gleisdorf Solar 2004).

[12] Isaksson et al., Report on technical investigations of large solar thermal systems, NEGST report WP2.D5 (2007).

[13] Reuss M., ZAE Bayern, Conference presentation at “Fachforum Solarstadt Munchen 2006”.

We consider that only conduction plays an important role in the heat transfer between neighbor elements. Energies transferred to the inferior element and from the superior element within a time step (p) are:

3.1 Energy input from the electrical heater

The auxiliary electrical heater has a 2kW power. Experiments showed that during heating water in the tank is mixed up in the entire volume just above the heater. We consider in this model that all elements are brought at the same temperature after one time step of electrical heating. Thus, the set-up temperature is reached by all elements above the heater in the same time, after one time step or more. If during a time step of heating the hot water temperature might rise above the set-up temperature, the electrical heater will stop even if the time step is not over.

Out of the large number of virtual case studies, a handy number of standard system configurations, which work best under different conditions, are identified. Based on these, the industry partners will provide consistent package solutions. These will enable planers and independent craftsmen to install reliable systems. The economical and ecological rating of the virtual case studies will also allow identifying the most promising markets, where systems are yet at the edge of economical breakeven point or beyond. Last but not least the results of the virtual case studies will be made available online with an easy to handle web-based tool, which can query it under different aspects.

3.3. Training on package solutions

Special training courses for solar thermal installers on standard system configurations and package solutions will be prepared and 15 pilot courses will be evaluated. Target group are (solar thermal) installers, because the goal of the packaged solutions is to avoid the need of engineering.

3.4. Dissemination, communication and training

Tailored dissemination, communication and training plans were elaborated to reach the different key actors. They include besides the presentation of results at relevant conferences and trade fairs addressing a wider audience (i) the dissemination of both the elaborated brochure and the online tool to query the virtual study cases towards professional groups (HVAC planners, architects, engineers, building industry), through their interest groups and associations (e. g. ESTIF, ECTP, chambers), where possible on the occasion of annual meetings or in synergy with related national and international projects, (ii) the provision of information and advice to (national) authorities on the potential of Solar Combi+ with the aim to include it in support programmes and (iii) the approach of local authorities in promising regions promoting pilot installations. Finally, information through public media in the most promising regions should give an important push to market entry. On the website all public deliverables will be available for download and most attention is given to the integration of the webpage in the existing information network on solar heating in general and combined solar heating and cooling in special.

4. Market analysis

In spite of an early settlement of the monitoring system, the STS has undergone a period of either reduced load and/or deficient operation, which has prevented the collection of a representative set of monitoring data enabling a thorough analysis to the system.

To the present, monitoring operations have suited particularly the detection of system faults, rather than evaluation of system behavior and performance. Nevertheless, and beside a short fault examples list, the data acquired allows a preliminary analysis of system performance and trends.

2.1 Data system results

The actual monitoring period started in June 2007, when the building was becoming occupied and starting to be close to project conditions. The deployment of the STS started three months before, with the solar field working at limited capacity considering the low occupancy of the building (only a single 4 collectors group uncovered on each orientation).

2.1.1. System Deficiencies

After the deployment of the system, a number of fault situations were detected; either related to installation problems or inadequate load conditions.

The system proved to be hydraulically unbalanced in its East-facing collectors.

There were leaks observed in the pumping area.

After the leakages were fixed and pressure reset they reappeared (after 1 month) as well as in the East-facing collectors.

S. Kaneko1* , M. Udagawa1 and T. Kusunoki1

1 Kogakuin University, 1-24-2 Nishi-Shinjuku, Shinjuku-ku, Tokyo, 163-8677, JAPAN
* Corresponding Author, dm07014@ns. kogakuin. ac. jp

Abstract

Total performance of solar hot water heating(DHW) system for an apartment house of 10 housing units was examined using the detailed simulation with EESLISM [4]. The simulation was carried out to examine the appropriate collector area and the storage tank volume for the central type of DHW supply system. The result for an apartment house showed that the collector area of 30-50m2 is appropriate to expect the solar contribution of 37.1-91.8% while the solar contribution is strongly depending on DHW supply rate. The appropriate storage tank volume is 1.0-1.5m3 in the studied cases. The economical efficiency of DHW system showed that the equipment cost should be suppressed below 2 million JPY if expecting the pay back period of 10 years.

Keywords: Collector area, Storage tank volume, DHW heating load, Equipment cost

1. Introduction

In the past studies [1-3], the solar hot water heating(DHW) system for an apartment house of 10 housing units was simulated in order to examine the difference of tilt angles and azimuths of the collector. In this study, in order to find the relationship of collector area and storage tank volume of the DHW system, the simulation study was carried out. The suitable combination of the collector area and the storage tank volume with considering initial cost are examined by simulating the yearly performance of the solar DHW system for the apartment house.

The simulations of the base case were calculated with a comparably small rise in energy prices of

1.3 %/a for natural gas and 0.3 %/a over 20 years for electricity [6]. However the current development of prices in Germany amounts to 9.7 %/a (non inflation-adjusted) over the last seven years [7] which indicates a higher annual rate of growth.

Therefore the rise in energy prices has been varied between

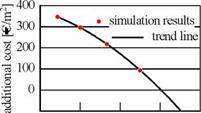
1.3 %/a and 7.5 %/a. Figure 3 (e) shows that as expected the lowest values of the objective function get smaller with a growing rise in energy prices which means that the heat generation costs per kWh become smaller. More surprisingly, the dimensions of each optimal system in terms of the underlying objective function and therefore also the primary energy savings stay constant, showing that the dimensioning does not depend on the rise in energy prices within the examined range. Figure 5 shows an extrapolation of the simulation results calculated with different rises in energy prices. The trend line derived from the calculated points indicates that the analysed solar heating system would be economically rewarding with a rise in energy prices of 9 %/a without any subsidies.

4.3 Subsumption of simulation results

Reducing the price of the solar collectors by 30 % improves the cost/benefit ratio by 21 %. The resulting optimal collector area increases by 3.5 m2, whereby the storage device capacity keeps unaltered. Using a high efficiency flat-plate collector instead of the initially defined model reduces the cost/benefit ratio by 8 %, whereas a low efficiency flat-plate collector increases the cost/benefit ratio by 13 % without having stronger impact on the dimensioning of the system. A 40 % reduction in the storage cost improves the cost/benefit ratio by 24 % again without changing the optimal dimensioning. The difference in the cost/benefit ratio between a system with 7.5 cm of storage insulation and a system with 17.5 cm of storage insulation amounts to 21 %, whereas the optimal system with the thickest isolation consists of a storage 120 litres larger than the thin isolated tank, connected to solar collectors that are 3.2 m2 smaller than the pendant with the thin isolated tank. Considering a rise in energy prices of 7.5 %/a instead of 1.3 %/a leads to a reduction of additional costs of 250 € /a with equal dimensioning parameters.