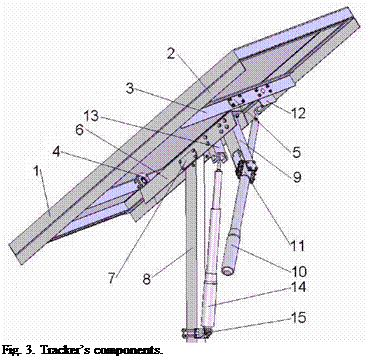The equatorial tracking system with linear actuators developed on the platform of Transilvania University of Bra§ov is presented in fig. 3. Panel 1 is assembled on a frame made of L profiles 2 mounted along the panel welded together by another two L profiles numbered 3. At the middle of the L profiles 3, bearings 4 and 5 together with the U profile central beam 6 create the daily rotational axis of the panel. The daily rotational movement (with angle P) is performed with the screw linear actuator 10, attached by the rotational link 11 on the rectangular beam 9 mounted with screws on the central beam. The end of the actuator’s screw is attached with rotational link on the bolt of the brida 12 mounted on the L profile 3.

The altitudinal (season) movement is performed around the rotational axis made of bearings 7 linking the middle of the central beam 6 with the pillar 8. The seasonal rotational movement (with angle y) is performed with the screw linear actuator 14, attached on the pillar 8 with the rotational link 15. The end of the actuator’s screw is attached with rotational link on the lever 13 mounted on the central beam 6.

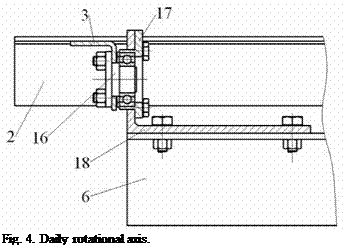
With the purpose of diminishing the friction, double sealed ball bearings are used for the main rotational axes of the tracking system. Figure 4 presents a longitudinal section through the bearing 4 of the daily rotational axis. The journal part 16, on which the inner ring of the bearing is mounted, is assembled on part 3. The cap 17, on which the outer ring of the bearing is mounted, is assembled on the part 18 belonging to the central beam 6.

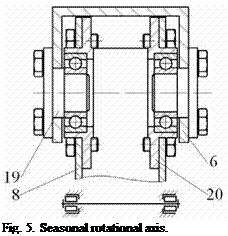
Figure 5 presents a longitudinal section through the bearings 7 of the seasonal rotational axis. The journal part 19, on which the inner ring of the bearing is mounted, is assembled on the central beam 6. The cap 20, on which the outer ring of the bearing is mounted, is assembled on the pillar 8.

Fig. 6. Specific positions.

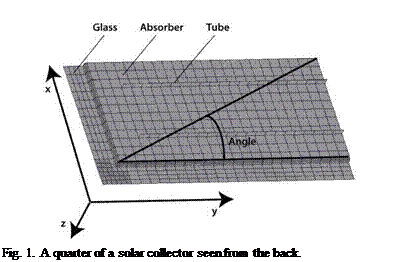
All calculations started out from common used design, dimensions and material of existing collectors. Sizes of 1 to 3 m2 were examined and different relations between length, width and height were investigated. The used directions of x, y and z can be seen in figure 1. The collector model consisted of a sheet of glass and an absorber formed as a tub where the edge of the tub was fixed on the glass sheet. The connection between glass and absorber in the model was the simplest possible where the absorber mesh was connected to the glass mesh as a "T" in an imagined cross section. The cavity was the volume between glass and absorber. All folds in absorber had a radius of 5 mm. The glass was sticking out 40 mm outside the absorber tub. 12 mm tubes with 0.85 mm material thickness were supposed to be placed on the backside of the absorber with a centre distance of 120 mm.

Material properties comes from soda glass, copper and aluminium. A complete list of used conditions can be seen in table 1.

2.1. Calculations

The Solar collector box had known dimensions, and it was possible calculate the volume enclosed by a list of faces (Venclosed) at different pressures. We supposed that when T=300K, the pressure inside

and outside of the box is 100kPa and all stresses in the material is 0. Then we wanted to find a P when T=500K. We used the ideal gas law for finding the pressure and volume at the new temperature.

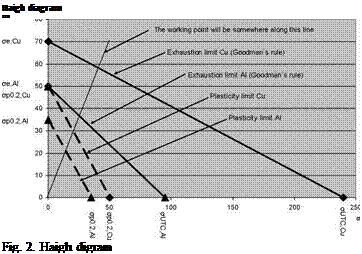Estimations of fatigue were made for having an understanding of if the stresses will imperil the function of the expected lifetime of the construction. A Haigh diagram, which can be seen in figure 2, is a help when doing valuations of fatigue.

The stresses are divided in to a static and a dynamic part. The static stress is put on the x-axis and dynamic stress on the y-axis. We use Goodman’s rule as the limit between the safe and the unsafe area[1]. Goodmans rule can be seen in (1).

Vtjts

The Goodman’s rule will give an line between (oUTs,0) and (0,oe) in the Haigh diagram. Plastic deformation is also unwanted; therefore a line representing that is added as an additional limit. The smallest value from Goodman’s rule and the plastic deformation line is then used as the safe area. [2]. The formula of the plastic deformation line can be seen in (2).

^ a, p0.2,allow ^ m, p0.2,allow ^p0.2

The plastic deformation limit will be a line between (op0.2, 0) and (0, op0.2). This means that the limit is op0.2 no matter the proportions between dynamic and static stress which gives us the allowable stress expressed as in (3).

^T 500, allow ^T 500,p0.2 ^p0.2

With table values of Copper and Aluminium, the maximum allowable stresses will become as in table 2 [2].

The small FracTherm® absorber had been mounted in a collector casing and tested as a stand-alone device, which means that interconnection between several collectors arranged in parallel had not been relevant. Therefore one important future task is to develop concepts for header channels and appropriate adaptors. It is important that the cross section of the headers is large enough in order to keep the pressure drop as low as possible and to ensure a uniform flow distribution in all collectors.

There are basically the following different possibilities to build header channels:

• Additional header tubes connected to the roll-bond absorber

• Wide, flat header channels integrated into roll-bond absorber (same height as absorber channels)

• Narrower, higher header channels integrated into roll-bond absorber (much higher than absorber channels)

• Other concepts generating channels by forming parts of the roll-bond absorber

These different concepts have to be investigated in detail especially with respect to feasibility, production tolerances, costs, pressure resistance, corrosion, coating, flexibility.

The FracTherm® algorithm allows generating channel structures on given areas which need not to be rectangular. One of the industry partners of the BIONICOL project already now offers custom-made non-rectangular collectors which fit the shape of the roof (Fig. 4, left). However, these are individually made meander absorbers, resulting in high production costs and high pressure drops in operation. With FracTherm® it is possible to generate channel structures which fit the given boundary form and lead to a uniform flow distribution as well as a low pressure drop (Fig. 4, right). Since roll-bonding is a series production process, it will not be economical to produce individual absorbers, but it would be possible to offer some standard non-rectangular absorbers which might be adapted to customers’ specifications to a certain degree.

The collectors developed in the BIONICOL project will be tested at Fraunhofer ISE. The collector performance tests will be carried out with aluminium roll-bond prototype collectors with different absorber designs (meander absorber, harp absorber, FracTherm® absorber) as well as with state-of-the — art collectors for comparison. The tests will be carried out according to the European standard EN 12975 (collector efficiency curve, exposition test, rain penetration test, internal and external thermal shock test, pressure drop). Moreover, the emptying behaviour of the collectors will be tested

and optimized which is important with respect to stagnation behaviour and a potential application in drain-back systems. Stagnation tests can be carried out using the indoor solar simulator of Fraunhofer ISE (determination of steam penetration depth, “steam producing power”, volume of fluid remaining in the absorber).

Field test collectors will be produced in a small-scale series production and installed in different test sites in Europe (maritime, urban, rural and industrial atmosphere). The field test collectors will be operated for one year. It is planned to publish the results of the final evaluation in several workshops.

S. Heft*, P. Di Lauro, S. Rose and M. Rommel

Fraunhofer Institute for Solar Energy Systems ISE, Heidenhofstrahe 2, 79110 Freiburg, Germany
* Corresponding Author, Stefan. Hess@ise. fraunhofer. de

Abstract

There is a high potential for the integration of solar generated heat into industrial processes or systems for air-conditioning. Important aspects to select the suitable collector technology for a specific application are the required working temperature of the solar loop and the corresponding effectiveness of the collector. But also the energy gained by a specific collector technology throughout the yearly operation has to be simulated before a clear decision can made.

Considerable work was done within IEA-Task 33/IV, SHIP (= Solar Heat for Industrial Processes), to collect information, initiate new developments and characterise collectors for medium temperature applications (80°C — 250°C).

At the lower medium temperature level (80°C — 150°C) plannings often apply vacuum-tube collectors because of their low heat losses. As a result of the previous SHIP — work, also advanced flat-plate collectors look promising. If the area for mounting the collectors is not restricted, advanced flat-plate collectors can offer technical and/or economical benefits compared to vacuum-tube collectors at the required temperature.

Additionally, there are many possibilities to develop collectors up to 250°C if concentrating reflectors are used. Low-concentrating CPC collectors do not require sun-tracking and achieve the highest possible concentration within their acceptance-angle. Concentrating solar radiation can reduce heat losses per absorber area and therefore achieve higher temperatures, even if the collector is not evacuated. A proper orientation is important to assure these features throughout the yearly operation.

Keywords: concentrating solar collector, SHIP, solar cooling, process heat

1. Introduction

Solar thermal collectors are usually the most cost intensive component of the heat production sub-system of solar supported processes. For a first estimation of the suitable collector technology for a given process, the most important aspects are:

• The efficiency of different collector-types at the required working temperature of the solar loop

• Necessary collector area per nominal heating/cooling capacity in m2/kW and the collector costs in EUR/m2

Methods for an estimation of these values are given in [1] and [2]. In the past, planners of solar thermally driven cooling systems or solar process heat applications often simply compared flat — plate collectors to evacuated tube collectors. Because the required temperatures for the support of industrial processes are highly different, the following discussions will be made on the basis of

different technologies for solar air conditioning. This way the application fields discussed about can be restricted to certain temperature levels.

For absorption cooling systems standard flat-plate collectors often can not reach the required working temperature economically. Therefore vacuum tube collectors have been used in recent developments. The main drawback of this collector type is its significantly higher costs [3]. Considerable work was done within IEA SHC-Task 33/ Solar Paces IV, SHIP (Solar Heat for Industrial Processes), to initiate new developments and characterise collectors for medium temperature applications (80°C — 250°C). The Task started in December 2003 and ended in October 2007. The work carried out in the SHIP project showed, that as an alternative to vacuum tube collectors also advanced flat-plate collectors look promising to reach higher temperatures. Additionally, there are many other possibilities to reach higher working temperatures by the reduction of optical and thermal losses [4]. This paper gives a brief overview of possible mechanisms to reduce the optical and thermal losses and shows some of the developed collectors with their efficiency at different working temperatures.

The simulation measurements have been made in the days of the equinoxies and solstices, between the hours 6 AM and 6 PM. We used the following hypotheses for the simulation: the roof oriented South, у = 0; the inclination angle of the roof is equal with the latitude of the place, 5 = Ф = 45 deg; the sky is clear; the contribution of the diffuse radiation to the photovoltaic effect is inessential; the input aperture radius is R= 50 mm; the photovoltaic cell radius is r = 20 mm; the parabola’s parameter is p = 20 mm; the distance between the peak of the parabola and the cell is H0 =10 mm; the geometric concentration factor is Cgeom = 6.25; the paraboloid’s height is h = 62.5 mm.

We have obtained the following results :

— The incidence angles of the radiation on the input aperture vis a vis to the rotation axis of the paraboloid are presented in the Fig.3. The analysis of the Fig.3 evidentiates the following aspects relative to the angles of incidence: at noon, it varies between 1.5 degrees (autumn equinox) and 24.2 degrees (winter solstice).

— The orar variation of the direct solar radiation intensity is presented in Fig. 4. The solar radiation is minimum during the winter solstice, for all the hours and has the highest values at all the hours in the summer solstice.

— The density of the solar flow on the input aperture is presented in the Fig.5. The highest values are : 799.5 W/m2 for spring equinox, 792.5 W/m2 for autumn equinox, respectively 808 W/m2 for summer solstice and 495 W/m2 for winter solstice.

— The density of the concentrated solar flow, depending on the hour, on the solar energy receptor, is presented in the Fig.6. The highest values are : 2837.5 W/m2 for the spring equinox, 2830 W/m2 for the autumn equinox, respectively 1219 W/m2 for the summer solstice and 708 W/m2 for the winter solstice.

— The average optical concentration factor, < Coptic > x102, and average optical efficiency < Ioptic > x 102, depending on the month, is presented in Fig.7. The lowest values of the average

optical concentration factor and the average optical efficiency are in December and June and the highest values are in March, respectively in September.

The radiation’s concentration is efficient for incidence angles at which the proportion between flow density on the receptor and the flow density on the input aperture is higher than 1, Brec /Bconc > 1. In the morning and in the evening the incidence angle is high and the optical concentration factor is smaller than 1. If the incrementation step of the time is small, in the value table it is determined the angle at which the concentration factor is equal with the unity. It has been established that the maximum value of the incidence angle is 6max = ± 30.06 deg. For the given case, the environment that fills the concentrator is the air, n = 1, the maximum concentration is Cmax = 1/(sin 6max )2 = 3.98. In the Fig.8 is shown the variation of the efficiency depending on the month. The highest efficiencies are obtained in March (25.30%) and September (26.10%).

For the model collector a specially designed 10mm thick triple-wall sheet with channels for transport of water (Solarnor, NOR) was used as the polymeric absorber [5]. Black absorbers with solar absorptivity a of 0.95 and infrared emissivity s of 0.90 were considered. Heat transfer medium was water with a flow rate of 50 kg/(m2h). The collector was covered by a 10 mm polycarbonate twin-wall sheet with intrinsic air filled channels (width 9.5 mm; spacing layer thickness 0.5 mm) acting as an additional insulation layer. A theoretical thermotropic layer was attached to the back side of the glazing. For the considered thermotropic layer constant solar transmittance and reflectance values in the clear and opaque state were assumed. In the switching temperature range a steep switching with a linear change from the light transmission to reflection was chosen. Solar transmittance of the film in clear state was set to 0.90 or 0.85. In opaque state, the transmittance was assumed to decrease to values between 0.10 and 0.60. Absorption in the thermotropic layer was neglected. The air gap between collector glazing and absorber was 10 mm. The solar collector is confined by a 50 mm and a 30 mm thick insulation on the rear side and the lateral surface, respectively. As to solar collector position south orientation and an angle of 45° to the horizontal was selected. Ambient air temperatures of 0, 20 and 30°C were considered. Solar irradiations of 1000 and 1200 W/m2 were modeled.

3. Results and Discussion

Required compatibility with fullerene pigment, high as possible transmittance to infrared radiation, heat resistance and good mechanical behaviour lead to select epoxy silicone resin as binder which, with adequate additives to confer enough strength and durability to the final paint, forms the paint base.

The paints were prepared from epoxy silicon resin that was previously mixed with charges and additives. Three types of pigments were used: a mix of C60/C70 fullerenes, copper powder (particle size 63 and 90pm), and stainless steel powder with particle size of 3 pm. The introduction of the pigments in the initial base paint was made with the admixing of the pigments in a solution of the resin and n-butyl acetate in a rotating disperser at a constant speed of 700rpm min-1 until a

granulometry of 12pm was reached. The paints were applied to a copper substrate by a draw bar coater and by a spray technique in order to achieve thin coatings with lower thickness.

Some painted samples with paint including organic pigments, were submitted to accelerate aging tests, with exposure to UV radiation, in humidity conditions with accordance of ASTM G 154 standard and also of strength to humidity following the standard NB ENISSO G 270-1.

3. Results and discussion

Nanostructured multilayer thin films with titanium oxide already were subject of our work [4], but to avoid multilayer production complexity and eventually atomic diffusion between layers with time, at high temperatures, one of our present goals is to optimise optical properties of monolayer titanium oxide thin films with adequate thickness, composition and morphology, complemented in terms of absorption increment by organic pigment impregnation. For impregnation adequate pigments have to be selected in order to have absorption peaks located in solar spectrum and preferentially in wavelength range where our optimised titanium oxide film have less absorption.

On the basis of this strategy we prepared pigment-adsorbed single-layer TiOx thin films using a natural dye extracted from Sambucus nigra L.[3] (a mixture of anthocyanins) with an absorption maximum of 530nm. Anthocyanins belong to a group of natural dyes found in fruits, flowers and leaves of plants. Because anthocyanins show the color in the range of visible light from red to blue, it is prospected to become a high efficient sensitizer for a wide bandgap semiconductors. Due to the carbonyl and hydroxyl group presented on anthocyanin molecule [3], it can be bound to the surface of titanium dioxide porous film to produce sensitized TiO2 thin films for dye-sensitized solar cells (DSSC) applications [18].

However applied chemically over optimised titanium oxide coating, didn’t improve significantly solar absorption, but best titanium oxide coating, with one layer, graded in terms of oxygen content, have 88% of absorption and 7% of thermal emissivity, and we hope that absorption could be improved with a final very thin layer with less refractive index.

Pursuing the objective of low cost, easy application, high solar absorption and durability, with a minimum possible of thermal emissivity, work was also done with formulation of paints with organic pigments (C60/ C70) and with organic and inorganic pigment (Cu and steel), having epoxy silicon resin as binder, with higher transmittance to thermal infrared radiation. The paints obtained showed emissivity values sensitive to the thickness, with the best couple values for absorption, emissivity of 96%, 74% respectively, these achieved for paint with organic pigment and average thickness coating of 4pm, the minimum thickness attained by spray application over copper substrate.

A computer system with a software was designed to obtain air temperatures, velocities and solar radiation data in the classroom. Seven temperature readings were recorded. The graph in Figure 13, shows temperature readings for inside the classroom and air entering — existing the collector. The top vent air (air existing) temperature of the collector on the increase when the sun shines. The difference between the top vent and bottom vent air temperatures is maximum at peak solar collection time on the south (between 12.00-15.00). On clear days the temperature difference is about 25-28 °С. Moreover, air temperature existing the collector is about 25-27 °С higher than the inside temperature of the classroom. As seen in Figure 14 , The top vent air velocity is about 0.5-0.6 m/sn at the same hours.

Figure 13. The temperature readings for inside of the classroom and air entering-existing the collector. (21-22

March 2005)

2. Conclusion

In conclusion, the insulated backing of the solar collector serves the dual function of blocking heat transfer between the classroom and the back of the profiles (and air chambers) and insulating the window area to reduce heat transfer from the classroom to the outdoors. This system provides heat by convection during sunny hours and also reduces heat loss on overcast days. This suggested system has the advantage of not requiring any modification to the existing heating system or of occupying any interior space. The solar energy collector is easy to both install and remove as required.

References

[1] G. Z. Gedik, A. Koyun, T. Yilmaz, (2004). Utilization Of Solar Energy Systems For Retrofit Design Of School Buildings And An Example Application, A research project, The Scientific And Technical Research Council Of Turkiye (TUBITAK), Project No: IQTAG-I241.

[2] G. Z. Gedik, (2002). Utilization of solar energy systems for school buildings, (in Turkish), Symposium on clean energy, Vol 1, pp. 259-266, Istanbul.

[3] M. Meltzer, (1985). Passive Active Solar Heating Technology, New Jersey, Prentice Hall Inc.

[4] G. Z. Gedik, A. Koyun, T. Yilmaz, “Utilization of Solar Energy Systems for Retrofit Design of School Buildings and an Example Application” 4th European Conference on Energy Performance and Indoor Climate and 27th Conference of the Air Infiltration and Ventilation Centre (EPIC 2006 AIVC), Lyon, Vol.1, 115-120, 20-22 November 2006.

[5] G. Z. Gedik, A. Koyun, T. Yilmaz, “ An Experimental and Numerical Analyze of a Solar Collector”

3rd International Symposium On Environment, 22-25 May 2008, Athens, Greece

R. Casasola1*, D. Romero1, J. Alonso1, J. M. Cejudo2.

1 Isofoton, C/ Severe Ochoa n° 50, 29590 Malaga, Spain
2 ETSII, Universidad de Malaga, Plaza de El Ejido s/n, 29071 Malaga, Spain
Corresponding Author, r. casasola@lsofoton. com

Abstract

A possible way of increasing the efficiency of solar collectors is to optimize the heat transfer between the fluid and the inner surface of the absorber tubes. There are several approaches to solve this problem, but one of the simplest and cheapest solutions is the passive method. Enhancing the heat transfer by this procedure has received a strong attention during the last decades. Many studies have demonstrated that there is a significant increase in the Nusselt number by using different devices as flux breakers or turbulators. It has been well established that the turbulent flow created facilitates an efficient transport of heat to the tube wall. Passive methods have also the advantage that there is no need of additional external power. In particular, in this work we have studied the insertion of turbulators into the absorber. Based on previous studies that claimed a 50% gain of convective coefficient in copper tubes, a proportional increase of the collector efficiency is expected. Extensive empirical tests have been made to evaluate the effect of these elements in the collector efficiency, measured according to EN 12975.

Keywords: absorber, heat transfer enhancement, tabulator, efficiency.

1. Introduction

A solar absorber can be considered as a special type of heat exchanger. Industrial heat exchangers usually operate in turbulence or swirl flow, where their performance is higher than in laminar flow.

The aim is to increase the heat transfer between the fluid and the inner wall of the pipe. There are two main reasons to explain this energy transfer enhancement: the inherent higher transfer coefficients of turbulent flow and the larger effective heat transfer area.

According to the classical model of the flat plate solar collector [1], there are two main strategies to improve the collector efficiency: to increase the optical gain or to reduce the thermal losses. In the first group, we can enumerate the use of anti-reflective glasses, high absorbing coatings or new absorber designs. In the second group, double glazed collectors, selective coatings and better thermal isolation materials. Each of these alternatives have different advantages and disadvantages in terms of costs, final application, durability, appearance, etc.

The solution described aims to raise the optical gain. Considering the transmittance of the currently used glasses, and the absorption of the absorbing surfaces, the development of the solar collector technology has almost reached its limit. There are commercially available glasses with a 95% of energy transmittance and absorbing surfaces with a coefficient of 0.98. Therefore, it seems difficult to increase the efficiency in these directions. However, there is still scope for improvement by enhancing

the heat transfer between absorber and fluid. The typical absorber configuration with sheet and tubes can be improved. Moreover, this option has the important advantage of increasing the efficiency without raising the stagnation temperature, what reduces durability problems.

There have been numerous authors who have studied heat transfer enhancement by means of insertions into the tubes, mostly using air like heat carrier fluid. Promvonge and Eiamsa [2] described the use of twisted tapes and conical inserts, Ray [3] studied the use in square ducts, etc. Many experiments and theoretical analyses have been done and empirical correlations have been obtained.

In this article we have prepared an application of the use of tabulators in solar absorbers, using an empirical approach. We have selected the most promising alternatives in terms of material costs and processability, and we have made several tests to evaluate its effect in terms of collector efficiency.

Examples of integrated storage collector (ICS) of polymeric materials are displayed in Fig. 9 (a) shows an ICS with polypropylene casing and transparent insulation of cellulose triacetate. The ICS in (b) has a moulded storage container in polyethylene, glazing in polycarbonate and heat ex­changer in copper. Example (c) is a recent Brazilian ICS product with polymeric components and available in four different sizes. The ICS system in (d) consists of a cylindrical tank under a trans­parent dome of PMMA with an inner, upper shell of PC and an outer, rear shell of HD-PE. The storage tank is of stainless steel with selective coating and has reflectors of aluminium to the sides and below. A recent development is a glazed “solar store”, an inflatable, rollable take-away unit with 30 l volume, generally for DHW preparation and particularly for camping and caravanning holidays or for hot water preparation in remote locations (e).

2.2 Collector frame

The flexibility in design and shaping due to polymer processing techniques, low weight and easy installation are some of the major advantages of polymeric materials for collector frame and cas­ings. Fig. 10 (a) illustrates a deep-drawn collector casing in PC with bracket anchor for collector mounting. Example (b) shows a collector corner profile of glass-fibre reinforced plastics and ex­ample (c) collector-frame profiles in wood plastic composites. A collector with metal-based ab­sorber in form of a building-integrated roof tile of glass fibre reinforced plastics (UP+GD+MD) is presented in example (d). Within Subtask A of IEA-SHC Task 39 many other structural designs of polymeric applications for solar collectors have been reported, e. g. fittings, manifolds, applications at prototype level and patented ideas.