Aluminium has the best ratio of thermal conductivity to cost and is the best material for this application. A thickness of approx 1mm gives reasonable collection efficiency (with 150mm pipe spacing) and also sufficient flexibility to avoid closing up the pipe completely.

4. Suitable surface finish for absorber plate

The two options are either non-selective paint or a selective surface. Comparative tests have shown an advantage in collection efficiency of 10-15% for selective over non-selective surfaces. For this low cost application, a non-selective absorber is probably optimal.

5. Suitable back insulation material

Since the collector is built on top of a material e. g. wood which already has quite a low thermal conductivity, then the additional insulation requirements are modest. For this application, a reflective bubble polythene sheet was used. It is easily available

6. Suitable glazing

Twin wall polycarbonate is cheaper and lighter than glass. It is also tough and virtually unbreakable. Its optical transmission is reasonable and its thermal resistance is better than single glass. Modern polycarbonate with UV resistant coating should last for at least 15 years before replacement. Therefore twin — wall polycarbonate (10mm thick) was chosen for this application. Standard glazing bars for the polycarbonate were used to locate the sheet.

I. Zaharie*, I. Luminosu and D. Ignea

Departmental de Fizica, Universitatea “POLITEHNICA” din Timisoara
Bulevardul Vasile Parvan No.2, 300233, Timisoara, Romania7
*Corresponding Author: ioan. zaharie@fiz. upt. ro, izaharie@gmail. com

Abstract

The paper presents a numerical study, using its own the Ray — Tracer software, about optical efficiency, during equinoxes and solstices, of a static paraboloidal concentrator installed on the roof of a building. The roof is inclined with 45 deg and is oriented South.

The optical efficiency is maximum during equinoxes and minimum during solstices.

All these results are in concordance with the results reported in literature illustrating the fact that the proposed software tool is competitive.

Keywords: paraboloid, flow’s density, aperture, optical efficiency

1. Introduction

In the competition between classically obtained electric energy and photovoltaically obtained electric energy, the solar generated energy price is prohibitive because the materials are expensive and the efficiency is low. A solution consists in the concentration of solar light. Though, the using of concentrators that follow the sun is not a realist solution because the installation’s price is high and non-conveniable for users. As a consequence, there are used more cheap static concentrators that are also easy to use [1, 2, 3].

The Ray-Tracer software is using the Ray — Tracing method and is used to study the paraboloidal concentrator. The concentrator is of non-imaging type. The small dimensions paraboloidal concentrators are considered as architectural elements mounted on the houses roofs. The paraboloids walls are made out of very cheap plastic materials covered in void with nanometric film made of aluminium or silver. The reflexion coefficient, R, does not depend on the incidence angle and we consider for R the value, R=0.96. The concentrated radiation falls on the nanostructured photovoltaic cells located in the focal plan of the paraboloid. The efficiency of the photovoltaic cells increases from 14-16 % up to 24 — 30% [4, 5, 6, 7].

The crucial factor concerning the application of thermotropic glazing is the switching range. For thermotropic hydrogels, thermotropic polymer blends and thermotropic systems with fixed domains maximum switching ranges of 77%, 52% and 25% are achieved, respectively. According to this for an all polymeric flat-plate collector with twin-wall sheet glazing and black absorber thermotropic hydrogels, thermotropic polymer blends and thermotropic systems with fixed domains would limit maximum absorber temperatures to 75, 90 and 125°C, respectively (assuming 85% solar transmittance in clear state) [1]. This allows for the application of cost-efficient plastics with more or less advanced engineering properties and temperature-stability as absorber materials for solar collectors. However, no product is commercially available today, which exhibits switching temperatures, the switching performance and the long-term stability needed for solar thermal applications. Thus further research and development on thermotropic materials is required to make the systems ready for the solar thermal market.

References

[1] G. M. Wallner, K. Resch, R. Hausner, Solar Energy Materials and Solar Cells, 92 (2008) 614-620.

[2] P. Nitz, H. Hartwig, Solar Energy, 79 (2005) 573-582.

[3] A. Seeboth, J. Schneider, A. Patzak, Solar Energy Materials and Solar Cells, 60 (2000) 263-277.

[4] H. Watanabe, Solar Energy Materials and Solar Cells, 54 (1998) 203-211.

[5] P. Nitz, H. R. Wilson (2008). In Proceedings of 2nd Leobner Symposium Polymeric Solar Materials, Leoben, Austria, pp. XIII-1-XIII-6.

[6] K. Resch, G. M. Wallner, R. W. Lang, Macromolecular Symposia, 265 (2008) 49-60.

[7] A. Beck, T. Hoffmann, W. Korner, J. Fricke, Solar Energy, 50 (1993) 407-414.

[8] A. Beck, W. Korner, H. Scheller, J. Fricke, W. J. Platzer, V. Wittwer, Solar Energy Materials and Solar Cells, 36 (1995) 339-347.

[9] D. Chahroudi, (1995). US 5404245.

[10] D. Chahroudi, (1983). US 4389452.

[11] L. M. Geever, D. M. Devine, M. J.D. Nugent, J. E. Kennedy, J. G. Lyons, A. Hanley, C. L. Higginbotham, European Polymer Journal, 42 (2006) 2540-2548.

[12] K. Yamamoto, T. Serizawa, Y. Murakoa, M. Akashi, Journal of Polymer Science: Part A: Polymer Chemistry, 38 (2000), 3674-3681.

[13] G. M. Campese, E. M.G. Rodrigues, E. B. Tambourgi, A. Pessoa, Brazil Journal of Chemical Engineering, 20 (2003), no. 3.

[14] J. H. Lee, D. G. Bucknall, Journal of Polymer Science: Part B: Polymer Physics, 46 (2008) 1450-1462.

[15] H. Okamura, T. Maruyama, S. Masuda, K. Minagawa, T. Mori, Journal of Polymer Research, 9 (2002) 17­21.

[16] H. Okamura, S. Masuda, K. Minagawa, T. Mori, M. Tanaka, European Polymer Journal, 38 (2002) 639-644.

[17] WT. Wu, Y. Wang, L. Shi, Q. Zhu, W. Pang, G. Xu, F. Lu, Chemical Physics Letters, 421 (2006) 367-372.

[18] H. Uyama, S. Kobayashi, Chemistry Letters, 9 (1992) 1643-1646.

[19] A. Georg, W. Graf, D. Schweiger, V. Wittwer, P. Nitz, H. R. Wilson, Solar Energy, 62 (1998) 215-228.

[20] H. R. Wilson, SPIE, 2255 (1994) 214-225.

[21] H. R. Wilson, in Grassie K. et al. (Eds) Functional Materials — EUROMAT, vol. 13, Wiley VCH,

Weinheim, pp 221 — 233.

[22] J. Schneider, A. Seeboth, Materialwissenschaft und Werkstofftechnik, 32 (2001) 231-237.

[23] W. Siol, H. J. Otto, U. Terbrack, (1993). EP 0181485.

[24] W. Eck, H. J. Cantow, V. Wittwer, (1993). EP 0559113.

[25] E. Jahns, H. Kroner, W. Schrof, U. Klowdig, (1995). EP 0749465.

[26] A. Goetzberger, M. Muller, M. Goller, Solar Energy, 69 (2000) 45-57.

[27] H. R. Wilson, A. Raicu, P. Nitz, (1996). In Proceedings of Eurosun 1996, Freiburg, Germany, pp. 534-539.

[28] F. S. Buehler, M. Hewel, (1999). EP 0985709.

[29] C. Schwitalla, H. Godeke, H. Konig, (2002). EP 1258504.

[30] K. Resch, G. M. Wallner (2007). In Proceedings of ISES SWC 2007, Beijing, China, pp. 541-545.

[31] Informationsdienst BINE — Schaltbare und regelbare Verglasungen (2002), http://www. bine. info/.

• Applications with a great changing energy demand like weekend break in industrial processes (e. g. industrial laundry).

• Useful temperature levels at low radiation and low ambient temperatures (space heating).

• Need of air with high temperature level e. g. bakerys, burning in of coatings.

• Avoidance of humidity problems in buildings and condensation occurences in sensitive electrical applications. Also through the regeneration of sorption materials at daytimes.

• Applications with lightweight, water critical, or optical flexible requirements.

• Drying of sorption materials with high temperature.

• Drying applications (e. g. wood, food etc.).

• Heating of industrial or high rise buildings with large collector fields.

• Solar cooling: open-cycle desiccant evaporative cooling (DEC).

• Solar domestic hot water and space heating with a fin heat exchanger.

3.2 System Components

• Collector

• Fan

• Solar controller with temperature sensors.

Optional

• Heat exchanger, air — fluid (fluids are for e. g. water, oil, steam, chemical products).

• Storage tank e. g. with water, pebble beds or sorption materials.

• Solar radiation sensor to check the system.

2. Conclusions

At the Kollektorfabrik the series production of the solar air collector has started.

A new collector for the requirements of applications with high solar fraction without the risks of a stagnation state is available.

For private usage the collector is suitable for space heating and domestic hot water preparation. Especially holiday residences can be dehumidified while not occupied in order to avoid moisture while there is no risk of stagnation problems. During occupation the system can additionally provide domestic hot water.

For commercial and industrial usage the collector fits best for drying applications, solar cooling and large scale heat demand.

As seen in Figure 4 and 6, in case of the collector surface receives radiation from infrared radiation lamps, air entry is realized from the hole 25 but air exit from the holes 23,24,26 and 27 isn’t realized. Incoming air from bottom is advanced in a way in the air chambers of the collector but air exit (holes 23,24,26 and 27 in figure 6) from the top of the collector is unrealized. (Figure 7 and 8) The surface temperature values of the collector are given in Table 1. In such a case, the system isn’t constituted the stack effect.

The tested solar collector is a commercial product with a covered gross surface of 2.541m2. The test was carried out in the Test Station of IEE, CAS, located in Beijing, China, at 37.5° N latitude and at 116.7° E longitude. The test period reported was realized from May 17th to October 19th, 2007.

Figs. 2-6 present the main experimental results. Fig.2. shows lineal fit to test data for instantaneous efficiency curve and equation is provided. Fig.3. shows second order fit to test data for instantaneous efficiency curve and equation is also provided. All of these experimental data can be obtained under the steady-state measurement conditions according to ISO 9806-1. The instantaneous efficiency data is based on the gross area of solar collector and fluid flow rate used for the tests is 0.02 kg/m2.s. With the experimental data obtained in Fig.2. and Fig.3. and using the proposed equations (1)-(7), the following parameters were calculated for this day test: the highest nis 0.608 and the lowest nis 0.528.

Obviously when the inlet temperature is close to the ambient temperature, the heat loss of solar collectors will be less than its heat loss as the difference between the inlet temperature and the ambient temperature is very large. On the other side, because of the all-glass evacuated tube, the heat loss can be effectively reduced under the high temperature operation mode.

In Fig.4, different instantaneous efficiency curve in different months can be provided. Through this figure, the common situation of solar collectors operated during a long period can be predicted. In the past 5 months the ratio of the actual useful energy extracted to the solar energy intercepted by the collector can reach a comparatively high point. It means that this kind of solar collectors can work in a good condition and supply actual useful energy on a stable level. With the experimental results of several months, it is possible to obtain common sense and characteristic curves of solar collectors.

Fig.5 and Fig. 6 shows in a certain day the variation of instantaneous efficiency, the difference between inlet temperature and ambient temperature of solar collectors and solar irradiance. In Fig. 5 the whole variation trend to some extent which instantaneous efficiency match solar irradiance is similar, but in the afternoon there exits opposite direction between two factors. Because all-glass evacuated tube can reduce heat transfer from inside to ambient, the energy can be reserved effectively. Meanwhile, if the direct radiation from solar energy is decreasing, for example, the clouds shadow the direct radiation, the ratio will be increased in an opposite direction to the solar irradiance. This result can be demonstrated by the same variation trend between the temperature difference and solar irradiance from Fig. 6. In the day test all-glass evacuated tube solar collector shows the reliable stability and high quality to supply the actual useful energy, and it can keep a good performance. The average instantaneous efficiency can arrive at 0.74 during the day test from 9:45 in the morning to 17:25 in the afternoon.

2. Conclusion

In this paper, a comprehensible test method to determine the thermal behaviour of solar collectors has been carried out. Through this kind of test an overall thermal performance can be provided for the product, such as the fit equation of the instantaneous efficiency considering the influence of inlet temperature, ambient temperature and solar irradiance, actual operation condition in a long period and the relationship among efficiency, difference of temperature and solar irradiance. And then, the manufacturer will obtain the information in order to improve the thermal efficiency of solar collectors. At the same time, the information is also useful to design the ideal solar water heating system with all­glass evacuated tube collectors for engineers. This procedure test also allows comparing, under the same test conditions, systems with some changes, for example with different materials, absorber selective surfaces, as well as thermal insulation, in order to analyze the influence of these parameters and together with an economical study can offer to the manufacturer the convenience or not to implement this modification.

References

[1] J. A.Duffie, W. A.Beckman, (1991). Solar Engineering of Thermal Processes, Wiley, New York.

[2] ISO9806-1, (1994). Test Methods for Solar Collectors — Part 1: Thermal performance of glazed liquid heating collectors including pressure drop.

[3] EN 12975-2, (2001). Thermal Solar Systems and Components Solar Collectors Part 2: Test methods.

[4] GB/T 4271, (2000). Test Methods for the Thermal Performance of Flat Plate Solar Collectors.

[5] Perers B, Dynamic Method for Solar Collector Array Testing and Evaluation with Standard Database and Simulation Programs, Solar Energy 1993, 50:517-26.

[6] Zeroual A, A New Method for Testing the Performance of Flat-plate Solar Collectors, Renewable Energy 1994, 4:825-32M.

The polymer performance pyramid (Fig. 5) is ranking the various polymers according to price and temperature performance. Most polymers in the following collector examples are of commodity and engineering plastics. Generally, commodity plastics are used in high volume and for a broad range

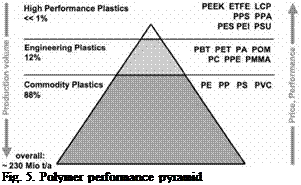of applications, e. g. packaging and house­hold products where mechanical properties and service environments are not critical. Such plastics exhibit relatively low me­chanical properties and low cost. Engineer­ing plastics are a group of plastic materials that exhibit good mechanical and thermal properties in a wide range of conditions. High-performance plastics have temperature resistance, strength, dimensional stability and chemical resistance even in demanding applications.

M. Meir*, J. Gjessing, J. Rekstad, N. Rumler[4]

University of Oslo, Department of Physics, P. O. Box 1048, N-0316, Oslo, Norway
Corresponding author: mmeir@fys. uio. no

Abstract

Passive ventilation was experimentally studied as overheating protection for polymeric collectors. The dimensions of the slit apertures, tilt angle and distance between collector cover and absorber were varied and the effect on the maximum temperature reduction was investigated. The longitudinal thermal expansion of the polymeric absorber was applied as trigger to open a ventilation flap if the absorber temperature exceeds a certain limit; sensitivity studies with the triggering of the flap were performed. A simplified method to determine the temperature dependent heat loss coefficient and the heat capacity of a glazed polymeric solar collector is presented. With this method the collector does not need to be connected to a heat removal system with circulating heat carrier. The method uses experimental data from the whole day, and is therefore not based on steady state conditions.

1. Introduction

Recently the interest has increased in using polymeric materials for solar thermal collector components, as cover sheets or absorbers (e. g. IEA-SHC Task 39). One reason among several is to utilize the flexibility offered by polymeric sheets and to design modular building units. These can substitute conventional roof or facade covers and simultaneously convert solar to thermal energy. Due to direct building integration the collector and the building share the thermal insulation and constructive parts of the building (support for the collector frame).

A serious limitation for this approach is the fact that if low-cost, low-/medium temperature performance plastics are chosen as absorber material in glazed solar collectors, the temperature of the absorber during thermal stagnation might be critical for the material and its service life. Thermal stagnation occurs for solar heating systems when no more heat is removed from the collectors (heat store is charged and controller stops the solar pump). If applied as absorber material in glazed collectors most actual polymers would therefore require a save and reliable overheating protection in the case of stagnation.

In the present work, the passive ventilation between collector cover and absorber is studied as overheat protection during thermal stagnation. Kearney et al. [1] and Roberts [2] have modelled corresponding passive ventilation processes, additionally with ventilation between absorber and thermal insulation. Kearney concluded that passive ventilation alone was not sufficient. This conclusion implied extreme desert climate with solar irradiance of 1100 W/m2 and ambient temperatures of 43 °C. Kearney and Roberts found that passive ventilation gave a reduction of the maximum temperature of 25-30 K for different absorber temperatures. Harrison et al. [3] have performed experimental studies with metal absorbers, where the backside of the absorber was cooled by ventilation. The authors measured a temperature reduction of approximately 30 K and propose thermally activated valves, which trigger the ventilation during stagnation and are closed

when the collector is operative. Another principle for a thermally activated ventilation flap is suggested in the patent [4] based on a hydraulic mechanism with low-boiling fluids. A different approach for overheating protection are thermotropic coatings, e. g. applied on the collector glazing; these coatings should switch from transparent to opaque at a critical temperature for the absorber material. Thermotropic coatings are under development and considerable R&D has been done, e. g. [5, 6, 7]. Another principle for the overheating protection is proposed in the patent by Griessen and Slaman [8]. The refraction index of the collector glazing, a prismatic structured optical layer, which is hollow inside, can be changed by a simple mechanism and reduce the transmittance for solar radiation. It should be mentioned that overheating is not only an issue for glazed polymeric collectors but also for glazed metal-based collectors [9].

If polymeric collectors are part of the building, sharing thermal insulation, the stagnation temperature and the collector efficiency vary from case to case. The present experiments allow a simplified method to determine the temperature dependent heat loss coefficient and the heat capacity of glazed polymeric collectors. The present work is based on the master thesis projects of Gjessing, 2006 and Rumler, 2007 [10, 11].

G. Moldovean 1*, R. Velicu 1, B. Burduhos1

1 Centre of Product Design for Sustainable Development, Transilvania University of Bra§ov, Romania
* Corresponding Author, ghmoldovean@unitbv. ro

Abstract

In order to improve the energy efficiency of PV or thermal collectors (panels), two possibilities are available: better materials and design for the solar energy absorber and the use of solar tracking systems. The paper presents the results of the embodiment design process of the main rotational axes of an experimental equatorial solar tracking system, with two rotational axis: a horizontal fixed axis and an inclined mobile axis. The system is one of ten different tracking systems for PV individual panels implemented, this year, in the campus of the Transilvania University of Bra§ov, Romania. It has been developed in order to research the optimization of the mechanical system of trackers as a meaning of improving the costs and energy efficiency of the system. There have been considered the loading cases depending on the functional positions of the tracking system (positions corresponding to minimum and maximum rotational angles), considering different distributions of wind pressure. Final constructive solutions, elements of preliminary design and conclusions on loads and loading cases involved in optimal embodiment design are presented.

Keywords: equatorial tracker, design, linear actuator, load

1. Introduction

The main advantage of using a tracking system is an increased amount of solar energy converted [1]. As disadvantages, it comes with its specific construction costs and also exploitation costs. An optimal design is mainly improving a tracking system by diminishing the costs of building and exploitation.

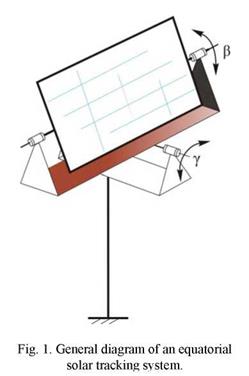
In order to perform a comparison between different solutions of tracking system, in the frame of a Project developed at Transilvania University of Bra§ov, a platform with 10 different tracking systems was developed. This paper is referring to an equatorial tracking system [2] (fig. 1). It has two rotational axes: a horizontal fixed axis (setting the у orientation angle) and an inclined mobile axis (setting the P orientation angle).

Rotation around the horizontal axis must be performed at an interval of few days (seasonal) and rotation around the vertical axis must be performed during each day, for a precise daily solar tracking. In order to perform both two movements the system is using linear actuators.

This paper is presenting a methodology of determining the loads involved in preliminary strength calculus of the elements of the tracking system and also some conclusions on the loading cases and their involvement in the specific loading of elements. The loading cases depend on the functional positions of the tracking system and also the loads caused by own masses, wind etc. (given by the specific of the region).

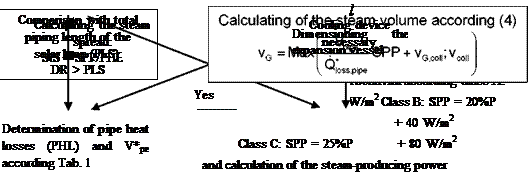The following schema (Fig. 3) illustrates the procedure for estimating steam-producing power, steam spread and steam volume:

Fig. 3: Simplified calculation schema to determine SPP, StS and SV and to dimension the expansion vessel

and cooling load.

With this empirical model, it is now possible to predict steam-producing power, steam spread and steam volume in the solar circuit for collector arrays of up to 30 m2.

References

[1] Hausner, R; Fink, C. (2003): Stagnation Behaviour of Thermal Solar Systems. In: Proceedings ISES Solar World Congress 2003. Goeteborg, Sweden.

[2] Scheuren, J; Kirchner, M.; Eisenmann, W. (2006): Reduction of Stagnation Load of Large-Scale Collector Arrays. In: Proceedings EUROSUN 2006, Glasgow, Scotland.