17.1. ОБЩИЕ СВЕДЕНИЯ

Метод математического моделирования приложен к ре­шению задачи анализа и оптимизации наиболее сложной гелиоустановки — солнечно-теплонасосной системы с се­зонным аккумулированием (СТНССА).

СТНССА характеризуются большим количеством вну­тренних и внешних связей. При проектировании и опти­мизации современных СТНССА необходимо учитывать множество технических и других ограничений.

Из изложенного следует, что возрастает значимость технико-экономических исследований по определению оптимальных параметров и структуры СТНССА, вида тех­нологической схемы и профиля оборудования на стадиях проектной разработки. Даже частичное решение этой про­блемы за счет приближения выбранных характеристик к оптимальным обеспечивает, как показали многочислен­ные исследования, высокий экономический эффект и, что немаловажно, повышает надежность системы.

Решение этих задач не возможно без математического моделирования. Реализация соответствующих математи­ческих моделей на ЭВМ позволяет проводить анализ и по­иск наиболее обоснованных проектных решений СТНССА.

Принципиальные преимущества математического мо­делирования, такие как возможность быстрого, точного, многократного решения задачи и оперативной корректи­ровки методики расчета, отвели ему определяющую роль в проектировании СТНССА и создании САПР, для которых необходимо специальное программно-математическое обе­спечение, реализуемое на основе выбранных математиче­ских моделей.

Однако анализ отечественных и зарубежных работ по внедрению методов математического моделирования в практику инженерных расчетов [18], показывает, что ме­тод математического моделирования нуждается в дальней­шем развитии и, прежде всего, в обобщении его основных принципов и способов применения, раскрытии на этой основе новых возможностей.

В последней четверти XX века для экономической и экологической оценки технических систем начали ис­пользовать методы эксергоэкономических исследований. Это новое направление научных исследований стало воз­можным благодаря работам R. Guggiolli [13], М. Tribus и R. Evans [14], Y. El-Saed [15], A. Bejan, G. Tsatsaronis, M. Moran [9], T. B. Морозюк [16].

Оптимизация любой энергосберегающей системы озна­чает вариацию структуры и параметров с целью миними­зации капитальных и эксплуатационных затрат при со­ответствующих технических и ресурсных ограничениях, обеспечении защиты окружающей среды, при доступности материалов, создании условий эксплуатационной надеж­ности и невысокой стоимости ремонта. Методы эксергоэко — номики показывают пути решения этих вопросов.

Как любая дисциплина, термоэкономика обладает специфической терминологией. Рассмотрим лишь основ­ные понятия и их определения, без владения которыми не­возможно дальнейшее знакомство с термоэкономикой [17].

Под переменными принято подразумевать величины, которые могут быть изменены с целью оптимизации. Чаще переменными являются термодинамические величины.

Действительная энергопреобразующая система состоит из большого числа элементов. Многие из них просты с точ­ки зрения моделирования (например, компрессор, турби­на, теплообменник), некоторые совмещают в себе функции нескольких компонентов (тепломассообменные аппараты). Для обобщения используется понятие компонент системы, то есть рассматривается наименьшая неделимая единица в составе системы.

В термоэкономическом (и особенно эксергоэкономиче — ском) анализе наиболее распространенными понятиями являются: топливо, продукт, деструкция эксергии, потери эксергии.

Под топливом подразумевается любой поток, входящий в компонент. Особый случай представляет компонент, в котором топливо является топливом для всей системы.

Выходящие из компонента потоки могут (в общем слу­чае) представлять:

— продукт — поток, направляющийся из рассматривае­мого компонента к последующему, для которого он будет являться топливом;

— деструкцию эксергии, которая в компоненте ассо­циируется с капитальными и эксплуатационными затратами (Z), связанными с размерами компонента. Понятие деструкции эксергии продемонстрируем на примере регенеративного теплообменника. Переход теплоты от «горячего» потока к «холодному» воз­можен только при наличии разности температур. В результате теплопередачи теплота с высокого темпе­ратурного уровня переходит на низкий, т. е. наблю­дается разрушение (рассеивание) эксергии. Разность температур, влекущая за собой наличие деструкции эксергии, определяет размеры теплообменной по­верхности, а следовательно, капитальные затраты, затраты на ремонт и обслуживание;

— потери эксергии, которые наблюдаются при рассмо­трении условий взаимодействия компонента с окру­жающей средой. Лучший пример — это теплопотери в окружающую среду от поверхности регенератив­ного теплообменника, имеющего температуру выше, чем окружающая среда.

На рис. 2.3 приведена логическая структура методоло­гии оптимизации с позиций эксергоэкономики [16].

Рис. 2.3.

Логическая структура опти­мизации энергосберегающей системы:

1 — синтез процесса; 2 — термо­динамическое моделирование;

3 — экономический анализ;

4 — базовый анализ; 5 — анализ каждого процесса и его оцен­ка; 6 — математические мето­ды оптимизации; 7 — эксперт­ные оценки и экспресс-оценка; 8 — оптимизация

Рассмотрим концепцию «информационно­

оптимизационной стратегии», сформулированную в виде обобщения принципов и постулатов термоэкономики за 40-летнюю историю ее развития [15].

Любая попытка усовершенствовать систему должна быть охарактеризована объективной функцией, критери­ями решения, которые являются степенями свободы для совершенствования системы, и подходом к проведению ее декомпозиции. Эти особенности не всегда независимы друг от друга. Их необходимо рассматривать одновременно, что и является реальным воплощением «информационно­оптимизационной стратегии».

Объективная функция (в денежных единицах) на ста­дии проекта — это стоимость продукции

J = T. cfF + hczZ + CR (2.23)

или чистая стоимостная функция

J = ‘LcfF + ‘LczZ-ЇСрР + CR, (2.24)

где J — стоимость (для уравнения (2.24) J — доход); сриср — та­рифы на единицу топлива F и продукта Р, сформированные рынком; cz — дисконтированные капитальные затраты от Z; Сл — постоянная стоимость остатка как функция от совер­шенства проекта. Когда предпроектная стадия переходит в
проектную, Сл может стать переменной для сравнения с дру­гими решениями, не зависящими от проекта.

Уравнение (2.23) применяется при анализе систем, про­изводящих более одного продукта, следовательно, необ­ходимым является определение стоимости каждого из по­лезных продуктов системы через распределение стоимости всего производства по каждому из них. Уравнение (2.24) предполагает использование рыночных цен на получаемые от системы продукты, а объективная функция может быть минимизирована (доход максимизирован) исключитель­но техническим совершенствованием системы. Необходи­мо отметить, что минимумы (максимумы) по уравнениям (2.23) и (2.24) не всегда совпадают.

В задаче минимизации стоимости энергетической си­стемы задействованы по крайней мере четыре составля­ющие: термодинамика {F, Р}, проектирование и произ­водство {Z}, экономика {cF, ср, cz}. Каждая составляющая имеет собственные методы формирования приведенных величин, следовательно, они должны быть представле­ны соответствующими моделями. «Информационно­оптимизационная стратегия» призвана разделить систему по двум уровням: уровню дисциплин и уровню компонен­тов, что облегчит в целом процедуру определения и приня­тия оптимального решения.

В качестве характеристики энергетической системы ре­комендуется принимать отношение стоимости полученной эксергии ZTX, заложенной в первоначальной стоимости вводимой энергии (топлива или электроэнергии), к сумме всех затрат на выработку положительного эффекта Z^E:

^вых

Ф = ^—• (2.25)

Если записать

(2.26)

то коэффициент ф можно представить следующим образом

г|ех — эксергетический КПД; £П — сумма потерь эксергии; Ebjl — вводимая в систему эксергия; и — энергетическая со­ставляющая затрат.

Коэффициент ф может относиться также к отдельному элементу системы:

ZT — £п,

Фі

где Eft. — переменная составляющая внутренней эконо­мики системы; к’« — постоянная составляющая внутренней экономики, которая в первом приближении в соответствии с работами [11, 16, 18] должна быть принята равной нулю.

Необратимость П, в системе описывается теоремой Гюи — Стодола как эксергетические потери

ZrWcpI^. (2.30)

і=і /=і

где AS, — возрастание энтропии.

Рассмотрим многокритериальную оптимизацию [19]. Примем, что оптимизируемая функция Ф имеет вид

Ф = (Х1,Х2,…,ХП).

Функция Ф гладкая, то есть непрерывная и имеет про­изводные в каждой точке. Следовательно, можно записать

_ ^ а®

<М> = Y—axt.

ti9Xt

Условие экстремума определяется тем, что независимо от выбранной переменной Хп

d0> = 0. (2.33)

Принимая во внимание, что не все переменные Хп явля­ются независимыми, следует записать систему уравнений

*№.4……. xJ = o;

V,(XlfX,……………………. Хл) = о,

… х„) = о,

где т — число уравнений связи; п — число переменных; (п — т) — степень свободы системы. Если степень свободы равна 0, то есть все переменные определены, то нет смысла рассматривать задачу об оптимизации.

Для того, чтобы определить, какие т являются зависи­мыми и какие (п — т) независимыми, используется метод Лагранжа. При этом система т уравнений примет вид

Поскольку имеем п уравнений, можно получить значе­ния т величин Xi из т уравнений. Оставшиеся (п — т) урав­нений вместе с исходными т образуют п уравнений, доста­точных для определения п значений Хг

В последние годы методы эксергоэкономического ана­лиза развиваются на базе теории информации. В таком случае функция распределения вероятностей определя­ется по заданным средним значениям величин. При этом используются следующие уравнения: сумма вероятностей,
связанных с определенными возможными состояниями, которая всегда должна быть равна единице; математиче­ское ожидание или его среднее значение предполагается известным.

Особый интерес представляет геометрический аппарат оптимизации. Этот метод нагляден и поэтому удобен для решения оптимизационных задач [16, 17].

Приведем основы теории С-кривых.

Примем, к примеру, что критерием оптимизации явля­ются затраты эксергии. Функция Z = f(EX) имеет миниму­мы по отношению к каждой из осей: ЕХт.„ и Zmi„ (рис. 2.4).

Оптимальное значение затрат (т. А) можно определить, предположив линейную зависимость между затратами эксергии АЕХ и затратами ДZ

AZ = kAEX, (2.36)

где к — капиталовложения на прирост первичной энергии.

При многокритериальной оптимизации используют метод С-поверхностей. На рис. 2.5 приведена поверхность, образованная С-кривыми по двухкритериальному анали­зу: термоэкономике и термоэкологии. При этом проекция экологоэкономики получена как замыкающая между тер­моэкономикой и термоэкологией.

Оптимальное значение анализируемой системы мето­дами С-кривых и С-поверхностей может быть определено графическим дифференцированием в границах рассматри­ваемого участка или построением касательной к кривым (поверхностям) а = arctgfe и определением соответствую­щей точки (на рис. 2.4 обозначено через min). Графический способ легко переводится в аналитический.

Для энергетической оценки технических систем наибо­лее целесообразно обращаться к методу эксергетического анализа.

Эксергия представляет собой количество работы, кото­рое может быть получено внешним приемником энергии при обратимом взаимодействии системы или потока энер­гии с окружающей средой до установления полного равно­весия [4].

По определению работа служит мерой энергии. Тем не менее, работа не обязательно является необходимым ко­нечным результатом, то есть целью действия анализируе­мой системы или потока эксергии. Конечным результатом действия анализируемой системы, кроме работы, могут быть преобразования теплоты, холода, получение нуж­ных параметров и т. д. В реальном процессе работа меньше уменьшения эксергии (в пределе работа может равняться нулю), так как часть эксергии не превращается в работу, а исчезает (вследствие диссипации энергии).

Между энергетическим и эксергетическим балансами имеется принципиальная разница. Энергетический баланс системы не отражает потери от необратимости процессов в анализируемой системе. Эти потери определяются эксер­гетическим анализом. При энергетическом анализе «поте­ря энергии» означает не потерю энергии вообще (энергия исчезать не может), а потерю ее для данной системы. Речь идет о невозможности или неэффективности использова­ния энергии из-за ее состояния или параметров.

В эксергетическом анализе учитывается исчезновение эксергии, то есть её уничтожение, связанное с диссипацией энергии. Эксергия подчиняется закону сохранения толь­
ко в обратимых процессах. В реальных системах эксергия может частично или полностью исчезать. Очевидно, чем меньше потери эксергии при прочих условиях, тем более эффективный в энергетическом отношении процесс про­текает в системе. Поэтому при сравнительном анализе не­скольких вариантов изучаемой системы следует выбирать вариант, который обеспечивает получение максималь­ной эксергии, то есть вариант с минимальными потерями эксергии.

В общем случае уравнение эксергетического баланса за­писывается следующим образом:

где 12=„ . — эксергия на входе в і-й элемент; 12 . — эксергия

на выходе из і-го элемента; AEV — изменение эксергии объ­ема; Li — работа, полученная или затраченная в і-м элемен­те; Епоті — потеря эксергии в і-м элементе.

Если объем потока не изменяется, то AEV= 0.

Отношение отводимой от системы эксергии — Евых к под­водимой эксергии 12вх определяет значение эксергетиче­ского кпд

(2.8)

При построении эксергетического графа следует учи­тывать следующее. Процесс сжатия рабочего тела сопрово­ждается возрастанием эксергии, а процесс расширения — ее уменьшением.

Эксергетический КПД реального процесса сжатия без отвода теплоты, но с внутренним трением, определяется по формуле

где ЕП — потери эксергии; hv h2 — начальное и конечное значения энтальпии в процессе сжатия.

Эксергетический КПД адиабатного процесса расширения

Заметим, что эксергетический КПД процесса расшире­ния отличается от адиабатного КПД: в С сопоставляются две характеристики одного и того же процесса, а в — ха­рактеристики реального процесса и идеального.

В задачах эксергоэкономического анализа и оптимиза­ции первостепенную роль играет теория и инженерная ме­тодика разделения физической эксергии потока рабочего вещества на термическую и механическую части с после­дующим определением каждой из них. Такой подход соз­дает предпосылки более корректному проведению оптими­зации методами эксергоэкономики [5].

Многие авторы предприняли попытку разделения фи­зической эксергии на термическую и механическую части [6-10]. Теоретические исследования не имели расчетных подтверждений, в связи с чем не нашли практического применения.

Разделение физической эксергии на термическую и ме­ханическую части графически впервые было иллюстриро­вано в диаграмме «эксергия — энтальпия» в [8] и развито в [4]. Следует признать, что построения в диаграмме e—h не являются объективными, как построения в диаграмме h—s, T-s или любой другой термодинамической диаграмме состояний. Диаграмма e—h создается относительно выбран­ной автором диаграммы точки 0(р0, Т0).

Объективность эксергетического метода термодинами­ческого анализа признана давно, однако все еще дискусси­онным является значение Т0, например, TQ = 288 К (15 °С) по стандартам ISO (США), Т0 = 290 К (17 °С) в [3] как стан­
дарт эксергетического анализа 1960-1970-х гг.; Т0 = 25 °С (77 °F, 298 К) как стандарт современной прикладной термо­динамики, широко используемый в [11].

Удельная физическая эксергия материального потока рабочего вещества определяется как

e = h-h0-T0(s-s). (2.11)

Если эксергия — работоспособность (максимальная ра­бота), то можно предположить, что существует абстракт­ная расширительная машина, в которой эту работу можно получить. Такое предположение представлено графически (рис. 2.1).

Если считать, что физическая эксергия представляет со­бой сумму термической и механической частей, то термиче­ская эксергия возникает при условии ТфТ0, механическая эксергия — при р Ф р0. Результаты анализа представлены в виде сложного уравнения, объединившего переменные в интегральном и дифференциальном виде, что дало возмож­ность сформулировать выводы лишь качественно без пер­спективы применения в инженерной практике.

Работа авторов [5] направлена на создание инженерной методики разделения физической эксергии на термиче­скую и механическую части.

Из всего множества термодинамических процессов су­ществует только один, в котором возможно осуществить исключительно процесс передачи теплоты. Это изобар­ный процесс теплообмена, который и будет использован для описания термической части физической эксергии. Известно, что изобарный теплообмен можно проводить при любом давлении, поэтому не существует ни теорети­ческих, ни практических ограничений для анализа этого процесса.

Из всего множества термодинамических процессов су­ществует только один, в котором возможно получить ис­ключительно механическую работу. Это изотермическое расширение. Изотермическое расширение в реальных условиях осуществить невозможно, однако описаны теоре­тические условия его проведения. Изотермическое расши­рение можно проводить при любой температуре Т, однако поддержание Т < Та или Т > TQ требует энергетических затрат. Кроме того, малейшее отклонение Т от заданной величины (в течение времени) нарушает стационарность процесса изотермического расширения, и в соответствии с рекомендациями, подробно изложенными в [6], такие про­цессы следует исключать из рассмотрения даже на уровне теоретического анализа. Таким образом, в дальнейшем будем использовать процесс изотермического расширения от р до р0 при Т0 = const для описания механической части физической эксергии.

Для создания аналитической модели разделения фи­зической эксергии на термическую и механическую части продифференцируем уравнение (2.11), используя исклю­чительно процессы изотермического расширения и изобар­ного теплообмена. Тогда

Известно [7-10], что для изобарного процесса

Ґде’

р const

Если представить dh = срдТ и вынести постоянную вели­чину теплоемкости ср за знак дифференциала, то получим выражение для определения термической части физиче­ской эксергии

^=ср{Т-Т0)-срТ0 n-

Для определения механической части физической экс­ергии ем представим величину е, используя уравнение (2.11). Тогда

dP = fy(h~ho — T0s+T0s0)T=co^dp. (2.15)

Поскольку величины hQ и TQsQ являются постоянными и определяют положение т. О, то они могут быть удалены из рассмотрения. Поэтому уравнение (2.15) можно перепи­сать в виде

Величина AhT=const является изменением энталь­пии потока рабочего вещества при его изотермическом расширении

а выражение L эр J3,_con3t — изменением

изотермическом

процессе расширения

Произведение T0Asr=congt описывает необратимость про­цесса изотермического расширения (по сравнению с адиа­батным) в терминах теоремы Гюи-Стодолы, то есть необхо­димость подвода теплоты.

При описании процесса изотермического расширения слагаемое

(Sh d

U-pJr. coiMt Р имеет знак «-» (производится работа), а слагаемое

я I dp

v PJr=conSt — знак «+» (подводится теплота).

Таким образом, выражение для механической части физической эксергии имеет вид

Проанализируем полученное выражение с точ­ки зрения применения его в инженерных рас­четах. Определение первого и второго слагаемо­го представляет значительные сложности ввиду необходимости использовать величину изобарной тепло­емкости. В процессах фазового перехода ср = оо для чистых рабочих веществ, для смесей рабочих веществ величина ср Ф const даже в состоянии переохлажденной жидкости или перегретого пара. Кроме того, величина Т в процессе изобарного теплообмена также является величиной пере­менной. Таким образом, для расчетов придется опериро­вать средним значением Т, правило определения которого должно быть дано дополнительно.

Решение поставленной задачи (2.12)-(2.20) было вы­полнено без учета конкретного расположения анализируе­мой точки, т. е. координат (Т, р, h, s). При интегрировании уравнений было принято условие, что нижний предел ин­тегрирования — координаты т. О {TQ, р0 ,hQ, sQ), верхний предел интегрирования — координаты анализируемой точ­ки (Т, р, h, s). Следовательно, по определениюр > р0, Т > Т0, h > hQ, s > sQ.

В соответствии с предположениями, принятыми в [12], представим графически (рис. 2.2) процесс расширения от анализируемой точки до т. О, в результате которого и будет получена работа, ассоциируемая с физической эксергией.

С точки зрения второго закона термодинамики величи­на As при расширении может быть: As > 0 (реальный про­цесс) или As = 0 (теоретический процесс). Видно, что рас­ширение от точки с координатами (Т, р, h, s) до т. О (Т0 , Po>ho> so)» гДе Р >Р0’Т> То’ h>hQ, s> sQ, противоречит второму закону термодинамики.

Таким образом, необходимо введение некоторого «ком­пенсирующего процесса», который позволит обеспечить As = 0. В качестве такого процесса выступает слагаемое

т

cpT0n— = As = (s-s0)

1° m

Тогда уравнение (2.20) может быть переписано в виде

Рис. 2.2.

К расчету термической и механической частей физической эксергии потока рабочего вещества: а — в диаграмме T-s; б — в диаграмме й-s

е~ср{Т То) (s s0) + T0(s s0) (h h0)T=conat. (о 9л

‘ % ‘ < ‘ 1 ‘

На первый взгляд, уравнение (2.21) можно упростить за счет объединения второго и третьего слагаемых. Одна­ко равны ли между собой значения энтропии s, входящие в них? Ответ на этот вопрос содержится в графической интер­претации (рис. 2.2) каждого из четырех слагаемых уравне­ния (2.21). Если термическая часть эксергии — это аналог теплоты, отведенной при р = const от Т до Т0, то величина sQ из второго слагаемого должна быть заменена величиной sA, то есть значением энтропии точки А с координатой (Т0, р, hA, 8а) до которой происходит изобарный теплообмен.

В результате проведенных замен в слагаемых, описы­вающих термическую часть физической эксергии, необ-
ходимо произвести некоторые коррективы и в слагаемых, описывающих механическую часть, так как процесс изо­термического расширения происходит от т. А до т. О. С уче­том всего вышеизложенного, принимая во внимание, что sA < sQ и hA < hQ, окончательно получаем выражение для определения термической и механической частей физиче­ской эксергии

e = {h—hA) — T0(s — sA) + T0(s0 — sA) — (h0 — hA)T=const. 22)

йг

На основании проведенного анализа по созданию тео­ретической модели разделения физической эксергии на термическую и механическую части, которая может быть использована в инженерной практике, сделан вывод, что необходимо иметь следующие данные вне зависимости от расположения рассматриваемой точки относительно т. О:

— термодинамические параметры рабочего вещества в рассматриваемой точке с координатами (р, Т, h, s);

— термодинамические параметры рабочего вещества в т. О (р0, Т0, h0, s0);

— значения энтальпии (hA) и энтропии (sA) во вспомога­тельной тЛ при рА=риТА = Т0.

Теория графов — область дискретной математики, осо­бенностью которой является геометрический подход к из­учению объектов и явлений [2, 3]. Она связана со многими областями математики — теорией множеств, математиче­ской логикой, комбинаторикой и пр. При исследовании графов случайных процессов используются методы теории вероятности.

Характеризуя проблематику теории графов, можно от­метить, что некоторые направления приложения этой тео­рии имеют более комбинаторный характер, другие — более геометрический. К первым относятся, к примеру, задачи о построении графов с заданными свойствами. Геометри­ческий (топологический) характер имеют многие группы задач. К ним относятся графов отходы, имеющие приложе­ния в технических и экономических задачах, а также гра­фов укладка, которые используются при автоматическом проектировании.

В теории графов существуют специфические методы решения экстремальных задач. Для конечных графов, т. е. для графов с конечным множеством вершин и ребер, про­блема существования алгоритма решения задач, в том числе экстремальных, чаще всего решается положитель­но. Построение эффективных алгоритмов, находящих ре­шение с требуемой степенью точности, для теории графов имеет существенное значение.

Для решения задач математического моделирования, анализа и оптимизации энергетических систем обраща­ются к топологическим моделям системы. Они позволяют установить зависимость между изменениями технологи­ческой топологии и количественными характеристиками изучаемой системы от входных переменных, воздействую­щих на систему.

Можно выделить четыре группы потоковых графов энергосберегающих систем: параметрические потоковые графы (ППГ), материальные потоковые графы (МПГ), те­пловые потоковые графы (ТПГ) и эксергетические потоко­вые графы (ЭПГ). При решении оптимизационной задачи для энергосберегающих систем в первую очередь будем об­ращаться к параметрическому потоковому графу.

Параметрические потоковые графы — это взвешенные по дугам и вершинам связные орграфы, отображающие пре­образование элементами исследуемой системы параметров физических потоков системы. Вершины параметрических потоковых графов отображают элементы (технологические операторы) системы, а также точки стыковки технологиче­ских трубопроводов, источники и стоки физических пото­ков системы. Вес каждой вершины соответствует системе уравнений математической модели изучаемой установки. Дуги параметрических потоковых графов соответствуют физическим потокам (массы, теплоты, энергии) системы.

Эксергетические потоковые графы — это взвешенные по дугам связные орграфы, отображающие преобразование элементами рассматриваемой системы расходов эксергии потоков вещества и энергии, а также потери эксергии в элементах системы. Вершины эксергетических потоко­вых графов соответствуют элементам (технологическим), преобразующим расходы эксергии, а также источникам и стокам эксергии, дуги — потокам эксергии и потерям эксер­гии в элементах системы. Вес дуг равен расходам эксергии. Для каждой вершины эксергетических потоковых графов справедливо уравнение баланса эксергии.

Материальные потоковые графы — это взвешенные по дугам орграфы, отображающие преобразование элемента­ми (технологическими операторами) массовых расходов физических потоков системы. Вершины материальных по­токовых графов соответствуют технологическим операто­рам системы, которые трансформируют массовые расходы физических потоков; точкам стыковки трубопроводов; ис­точникам и стокам вещества физических потоков. Дуги материальных потоковых графов соответствуют физиче­ским потокам энергетической системы (ЭС).

Тепловые потоковые графы — это взвешенные по дугам связные орграфы, отображающие преобразование элемен­тами системы потоков теплоты энергетической системы. Вершины ТПГ отображают элементы (технологические операторы), которые изменяют тепловые расходы физиче­ских потоков, точки стыковки трубопроводов, источники и стоки теплоты ЭС. Дуги ТПГ соответствуют физическим потокам теплоты.

Следует подчеркнуть, что кроме внешних источников теплоты могут быть и внутренние (фиктивные), например тепловой эффект, вызванный экзотермической химиче­ской реакцией.

Матричное представление графов позволяет отобразить структурные особенности графов.

Граф можно отобразить при помощи следующих ма­триц: ветвей ||L||, смежности ||Н||, циклов ||М||, отсечений ||N||, инциденций ||S||.

Топологический метод составления системы уравнений базируется на анализе топологических особенностей пото­ковых графов.

Материальному и тепловому циклическому потоковым графом определенной энергетической системы соответ­ствует матричное уравнение вершин, составленное для по­токов по дугам графа:

l|S|| х ||С|| = 0, (2.3)

где ||S|| — матрица инциденций циклического потокового графа, имеющая размер (R ж е), где R — ранг матрицы; е — число дуг; ||С|| — матрица-столбец потоков ЭС размера (е х 1).

Вместо матричного уравнения вершин (2.3) можно со­ставить эквивалентное матричное уравнение отсечений:

l|N|| х ||С|| = 0, (2.4)

где ||N|| — матрица отсечений графа, имеющая размер (R ж е).

Топологический метод следует применять к материаль­ному потоковому графу и к тепловому потоковому графу.

Если уравнения для всех материальных и тепловых потоковых графов образуют совместно разомкнутую си­стему уравнений, то получают ациклический информаци­онный граф системы уравнений балансов энергетической системы.

Если уравнения связей рассматриваемого потокового графа образуют совместно замкнутую систему уравнений,
то получают циклический информационный граф системы уравнений балансов энергетической системы.

При решении задач расчета балансов энергетической системы, для которых справедливы системы линейных уравнений материальных и тепловых балансов, топологи­ческий метод позволяет разработать ациклический инфор­мационный граф системы уравнений балансов энергетиче­ской системы.

Для анализа сложных встречно направленных энер­гетических систем следует обращаться к иной стратегии анализа. Алгоритм оптимального анализа сложной энер­госберегающей системы, отображаемой многократным параметрическим потоковым графом, представляет собой упорядоченный по слоям вершин эквивалентный ацикли­ческий параметрический потоковый граф. Его получают из многоконтурного исходного графа в результате разрыва минимального множества особых дуг Q*. Это устанавли­вает порядок расчета математических моделей отдельных элементов энергетической системы, соответствующих вер­шинам параметрического потокового графа.

Необходимо в исходном ППГ определить множество особых дуг

Q* = (?!, q2,…. qp), Q*<= Q, Q* =p, p^m (2.5)

с минимальной суммой параметричностей.

Для энергетических систем основным критерием эф­фективности обычно служит преобразование потоков энергии в системе, а также термодинамическая степень совершенства функционирования системы в целом и ее от­дельных элементов. При таком выборе оптимума решение определяется условием минимальных потерь энергии в системе:

ЪЕ = min.

ПОТ

Любая энергетическая система имеет определенную технологическую структуру, то есть состоит из ряда вза­имосвязанных элементов, характеризуется заданными параметрами, в том числе входными и выходными пере­менными, и взаимодействует с окружающей средой. Пре­жде чем сформулировать оптимизационную задачу, дадим определение основным характеристикам анализируемой системы.

Входные переменные системы (X) — это параметры входных технологических потоков системы, а также пара­метры окружающей среды (температура, давление, влаж­ность и пр.), которые оказывают влияние на функциониро­вание системы.

Выходные переменные системы (У) — это параметры выходных технологических потоков. Их подразделяют на параметры состояния потока (давление р, температура t, массовый расход т, объемный расход V и пр.) и параме­тры свойств потока (например, плотность р, теплоемкость с, вязкость р).

Состояние системы — это набор выходных переменных, которые полностью характеризуют функционирование си­стемы в каждый момент времени т. Совокупность наборов выходных переменных системы на некотором интервале времени Дт называется пространством состояний системы.

Технологическая структура системы — это строение и внутренняя организация системы, то есть состав элементов и взаимосвязи между ними. Технологическую структуру при записи математической модели формально можно оха­рактеризовать числом элементов Ng в системе, числом тех­нологических потоков ДГт п и законом взаимосвязей между элементами R. Технологическую структуру принято назы­вать также технологической топологией системы.

Конструктивные параметры системы (К) определяются геометрическими характеристиками конструкций элемен­тов системы (например, объем, площадь поверхности или сечения, длина, диаметр).

Технологические параметры системы (Т) — это физико­химические величины, определяющие процессы, проис­ходящие в системе (скорость движения массы, потоки массы, теплоты, энергии, коэффициенты теплопередачи и массопередачи).

Параметры технологического режима (Р) — это факто­ры, влияющие на режим процесса и на управление им.

Критерий эффективности (КЭ) системы (у) — это показа­тель, по которому можно оценивать степень соответствия системы для выполнения своих функций. Коэффициент эффективности используется для сравнительной оценки различных вариантов системы, а также для анализа, син­теза и оптимизации исследуемой системы. Одними из наи­более распространенных критериев эффективности явля­ются экономические критерии. К ним, в первую очередь, относятся приведенные затраты.

Для энергетических систем оценочным показателем служат потери энергии. Количественной и качественной характеристикой работоспособности потоков энергии в системе является эксергия. Для энергосберегающих си­стем основным критерием эффективности может служить результативность преобразования потоков эксергии в си­стеме, а также термодинамическая степень совершенства функционирования системы и ее отдельных элементов.

Анализ и оптимизацию энергетических систем следует основывать на методе системного анализа [1]. Теория си­стем характеризуется следующими особенностями:

— система представляет собой совокупность элементов, которые, в свою очередь, в зависимости от структу­ры технического объекта могут рассматриваться как системы;

— для систем характерно наличие интегральных свойств, т. е. свойств, присущих лишь системе в целом, но не свойственных ни одному из ее элементов в отдельности;

— для любых систем характерно наличие существен­ных связей между элементами, что дает возмож­ность выделить систему в виде целостного самостоя­тельного объекта.

Наиболее рациональный путь изучения системы — пред­ставить ее в виде модели, что значительно облегчает ана­лиз системы.

В соответствии с методом системного анализа в процес­се исследования можно выделить следующие этапы.

А. Построение модели, т. е. формализация исследуемо­го процесса или явления. Этот этап предполагает описание процесса при помощи математической модели.

Формальное описание системы следующее. В каждый момент времени теГна вход в систему поступает вход­ной параметр х(т), который представляет собой вектор X = (Xv Х2, …, Хт) в /n-мерном пространстве входных параме­тров X. В этот же момент времени на систему воздействует внешняя среда, которая описывается л-мерным вектором U = (Uv U2,…, Un) в пространстве действия параметров U.

Система характеризуется набором внутренних, т. е. соб­ственных параметров П = (Пх, П2, …, ПА). Совокупность внутренних параметров может рассматриваться как век­тор в fc-мерном пространстве параметров П.

В каждый момент времени система находится в некото­ром состоянии Z(t). Начальное состояние обозначим через ZQ.

Выходные параметры системы в некоторый момент вре­мени є Т, где тс > т„, в пределах времени т0 — тс определя­ются соотношением

y(.tc) = F[i, z0, х(т),П(т),Щт)]. (2.1)

Для систем, состоящих из нескольких подсистем, всю установку расчленяют на конечное число частей (основных элементов установки) и формулируют задачу для каждой части (элемента) системы. При этом следует учитывать связь между этими частями.

Б. Постановка задачи, то есть описание операции. При этом следует сформулировать оптимизационную задачу

/ (лс) -» max, х є Е, (2.2)

где х — элемент некоторого нормированного пространства Е, определяемый природой модели, G <= Е — множество, определяемое структурой модели и особенностями иссле­дуемой операции.

Задача исследования трактуется как некоторая опти­мизационная проблема.

В. Решение сформулированной задачи. Могут быть при­няты разные стратегии оптимизации. Критерием должна служить наиболее экономичная стратегия из числа вы­бранных предварительно, которые удовлетворяют всем

принятым ограничениям и обеспечивают достижение по­ставленной цели.

При исследовании сложных энергетических систем объект структурируют, рассматривая его как систему вза­имосвязанных элементов с учетом присущих им собствен­ных характеристик и процессов [1].

Для сложных энергетических систем со сложной техно­логической схемой при решении оптимизационной задачи рекомендуется обращаться к двухиерархической модели. Исходя из первичной модели, строят упрощенную модель изучаемой системы, которой свойственны менее жесткие ограничения и критерии. При помощи упрощенной моде­ли устанавливают основные параметры системы, ее кон­струкции. Это позволяет определить основные проектные решения. После этого, приступая к анализу более сложной исходной модели, находят более точное решение для ис­комых количественных показателей исследуемой системы.

Пассивные гелиосистемы используются только для ото­пления. Их кратко называют ПССО — пассивные системы солнечного отопления. В этих системах теплота поглоща­ется и аккумулируется самими строительными элемента­ми здания, а распределение ее в отапливаемом помещении происходит чаще всего естественным путем. Пассивная си­стема отопления отличается простотой, ее эффективность достаточно высока — она обеспечивает до 60 % отопитель­ной нагрузки [56, 132].

Принцип пассивного использования солнечной энер­гии состоит в непосредственном нагревании ограждающих конструкций солнечной радиацией с последующей переда­чей теплоты в обогреваемое помещение.

Обзор литературы [3, 9, 51, 132] позволяет выделить следующие типы пассивных систем солнечного отопления:

— открытые (прямое облучение);

— закрытые без циркуляции теплоносителя (система Моргана);

— массивные системы: стена Тромба-Мишеля (с экра­ном и без экрана); закрытые системы с аэродинамическим затвором; стена Лефевра; с аккумулятором (в грунте или в объеме здания) и с воздушным теплоносителем; оранжерея.

а — без экрана; 6-е теплоприемным экраном; 1 — остекление; 2 — стена здания; 3 — циркуляционные кана­лы; 4 — теплоприемный экран
1 — стена; 2,6 — входной и выходной воздушные каналы; 3 — межстеколь­ное пространство; 4 — стекло; 5 — те­плоприемный экоан; 7 — тепловая изоляция; 8 — аэродинамический затвор

Рис. 1.72.

Система Лефевра:

1 — остекление; 2 — теплона­копительная стена; З — тепло­изоляция; 4 — теплоаккуму­лирующее покрытие

В открытых системах солнечные лучи попадают в по­мещение через увеличенные оконные проемы и нагревают строительные конструкции. Последние становятся прием­никами и аккумуляторами теплоты.

В закрытых системах поток солнечной радиации по­глощается мощной ограждающей конструкцией, которая одновременно является аккумулятором теплоты.

Недостатком открытых систем является неустойчивость теплового режима, сильная зависимость от солнечной ин­соляции (рис. 1.68). Поэтому большее распространение по­лучили закрытые системы солнечного отопления. Здание с пассивной системой без циркуляции теплоносителя было построено А. Е. Морганом в 1961 г. (рис. 1.69). В дневное время поток солнечной радиации нагревает массивную сте­ну здания, а в ночное время эта теплота передается поме­щению. Как показал опыт эксплуатации здания, внутрен­ний воздух в помещении нагревается неравномерно.

Более удачное решение представляет собой система Тромба-Мишеля. Такой «солнечный дом» имеет различ­ные конструктивные решения (рис. 1.70, 1.71). По анало­гичному принципу построена система Лефевра (рис. 1.72). Верхняя часть наружной стены, ориентированной на юг, имеет двухслойное остекление. Наружная стена вместе с перекрытием являются аккумуляторами теплоты.

Схемы установок с аккумулированием теплоты показа­ны на рис. 1.73.

Теплоаккумулирующая стена может быть выполнена в виде контейнеров, заполненных водой. Накопленная кон­тейнерами теплота солнечной радиации передается в поме­щение за счет конвекции (рис. 1.74, а).

Другой вариант такой системы отличается тем, что пло­ская крыша используется в качестве водяного аккумуля­тора и называется «скайтер» (рис. 1.74, б).

Разновидностью системы с контейнерами, заполненны­ми водой, является, так называемый, термодиод. Он состо­ит из двух контейнеров с водой, разделенных слоем изоля­ции и соединенных между собой вверху и внизу трубчатым канатом (рис. 1.75).

Вариант совмещения пассивной гелиосистемы с акку­мулятором при свободной циркуляции воздушного тепло­носителя показан на рис. 1.76.

Весьма перспективно в России внедрение так называе­мого «солнечного» жилого дома. Это позволит снизить энергопотребление на нужды фермерского домашнего хо­зяйства до 15 % настоящего уровня. В качестве примера рассмотрим потери теплоты, кВт’ч/год, жилого дома пло­щадью 120 м2 в сельской местности на широте 55-60° [77].

При сооружении здания с ПССО следует учитывать ряд требований, предъявляемых к этим системам.

Необходимо уточнить ориентацию здания, его распо­ложение на местности с учетом климатических условий данного региона и степень инсоляции всего здания, а так­же влияние здания на существующую застройку и влия­ние окружающей среды на здание. Если гелиоприемники расположены на южной и восточной стенах, то восточная стена, например, может полностью затеняться рядом стоя­щим зданием. В этом случае следует менять ориентацию «солнечного дома».

Весьма существенно проанализировать тепло­вой баланс здания с целью уменьшения до мини­мума потерь теплоты, в том числе неоправданных. К примеру, можно сократить площадь оконных проемов, уменьшить неплотности в оконных проемах и наружных ограждениях.

Эффективность и надежность пассивной системы в зна­чительной степени определяется поглощающей способно­стью стены теплоприемника. Его, как правило, покрывают черной краской.

Если аккумуляторы сооружаются в грунте или в объеме здания, то необходимо учитывать теплоемкость материала аккумулятора; выбирать наиболее рациональные режи­мы подачи и отбора теплоты; размещать аккумулятор так, чтобы исключить неоправданные потери теплоты. Следу­ет принять во внимание, что размещение аккумулятора в грунте требует, как правило, механической вентиляции для транспортировки воздуха [14, 15]. Размещение акку­мулятора в объеме здания дает больший эффект, так как теплота от аккумулятора направляется непосредственно в помещение. Однако такой аккумулятор довольно сложно вписать в объем здания [9].

Метод расчета пассивных систем солнечного отопления приведен в работах [2, 9, 56].

Часть 2

Схема теплохладоснабжения установки с абсорбцион­ным термотрансформатором показана на рис. 1.63. Ис­точником энергии служат ветродвигатель и солнечная

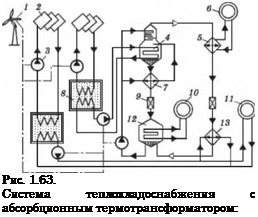энергия. Схемой предусмотрено наличие аккумуляторов теплоты [131].

1 — ветродвигатель; 2 — солнечные коллекторы; 3 — насосы; 4 — генератор с дефлегматором; 5 — конденсатор; 6,10- потребитель холода; 7 — теплообмен­ник раствора; 8 — аккумулятор теплоты; 9 — дроссельные вентили; 11 — по­требитель теплоты; 12- абсорбер; 13- испаритель

В связи с необходимостью иметь наипростейший вид рассматриваемой схемы в теории графов применяется ме­тод эквивалентирования. Это замена реальной системы или ее элементов некоторой приближенной, абстрагирован­ной, упрощенной моделью, эквивалентной относительно функционирования и свойств. Этот принцип рассмотрения системы необходим ввиду практической невозможности количественно описать некоторые элементы и связи с по­мощью существующих математических методов.

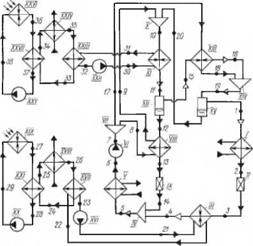
На рис. 1.64 представлена информационная схема си­стемы солнечного тепло — и хладоснабжения, для прочте­ния которой воспользуемся табл. 1.2.

Потоковый параметрический граф и соответствующая ему матрица инциденций представлены на рис. 1.65. Этот граф удобен для организации расчетов и анализа свойств си­стемы как при «ручном» расчете, так и при расчетах на ЭВМ.

Если рассматриваются более простые схемные решения (без аккумулятора теплоты низкого потенциала, без ветро­энергетической установки и пр.), то соответствующие эле­менты и связи в информационной схеме «отключаются» и приравниваются нулю вершины и дуги в графе.

Граф (рис. 1.65) состоит из трех блоков с двумя точками сочленения — III и XI. Декомпозиция графа по этим точ­кам приводит к трем порожденным подграфам, которые описывают топологию каждой ветви отдельно, т. е. описы­вают абсорбционный тепловой насос, высокопотенциаль­ную и низкопотенциальную системы солнечной энергии.

Связность графа прослеживается внутри каждого кон­тура. Таким образом, разрыв связей 21 и 22 вершины III и связей 30, 31 вершины XI не противоречит теории графов и дает возможность анализировать каждый контур отдель­но. Аккумуляторы теплоты поддерживают на постоянном уровне параметры потоков 21, 22 и 30, 31, следовательно, при расчетах теплонасосного контура эти параметры мож­но считать заданными.

Высокую эффективность работы рассматриваемой си­стемы солнечного тепло — и хладоснабжения можно полу­чить при использовании высокопроизводительных абсорб­ционных тепловых насосов с большой степенью внутренней регенерации. В этом случае, в зависимости от заданных входящих и выходящих потоков (для потребителя), можно оптимизировать работу абсорбционного теплового насоса по минимальной теплоте генерации и приводной электри­ческой мощности для насоса. Тепловой насос подвергается глобальной оптимизации в локальной для системы зоне.

Традиционно математическая модель должна пройти экспериментальное подтверждение. Если модель построе­на на основе теоретико-графовых методов, то отпадает не­обходимость в создании полной системы. Вполне достаточ­но проверить адекватность модели на отдельном элементе по математической модели этого же элемента.

Адекватность математической модели системы сол­нечного тепло — и хладоснабжения проверена на примере

Рис. 1.65.

Потоковый параметрический граф и матрица инциденций схемы, приведенной на рис. 1.64

солнечных коллекторов разных конструкций. Для выпол­нения автоматизированных расчетов разработаны эксерге — тический потоковый граф гелиосистемы и соответствую­щая ему матрица инциденций (рис. 1.66).

Рис. 1.66.

Эксергетический потоковый граф и матрица инциденций для гелиосистемы

Для максимального охвата территории страны, где целесообразно применять гелиосистемы, авторами при­няты следующие климатические условия: 40° с. ш., 52° с. ш., 56 ° с. ш.

Испытываемые гелиоколлекторы имели одинаковые размеры и равные условия проведения испытаний. Экс­перимент проводился с тремя конструкциями поглоща­ющих панелей солнечных коллекторов: плоской, листо­трубной и трубчатой на стенде-иммитаторе солнечного излучения. Результаты проверки адекватности матема­тической модели солнечных коллекторов показали хо­рошее совпадение расчетных и экспериментальных дан­ных (рис. 1.67).

Рис. 1.67.

Результаты эксперимен­тальных и расчетных данных зависимости т] = f(R), где R — тепловое сопротивление

На рис. 1.60 приведена схема гелиоустановки системы теплоснабжения. Источником энергии для теплового насо­са служат солнечная энергия и низкопотенциальная тепло­та грунта. Для более равномерного теплоснабжения потре­бителей схемой предусмотрена система аккумулирования теплоты.

Рассматриваемую систему можно представить как сово­купность вершин (элементов системы) и дуг (физических потоков между элементами). В этом случае получаем па­раметрический потоковый граф (ППГ), который является топологической моделью системы. Пользуясь ППГ, строят эксергетический потоковый граф (ЭПГ), который сохраня­ет топологическую модель, но дополнительно учитывает потоки эксергии.

Представление ЭПГ как Е(А, Г) позволяет указать мно­жество вершин, связанных эксергетическими потоками с какой-либо отдельно рассматриваемой вершиной.

Потери эксергии П. в произвольной вершине графа Е(А, Г) определяются алгебраической суммой значений дуг

графа, отрицательно или положительно инцидентных рас­сматриваемой вершине. Для цифрового описания ЭПГ ис­пользуют матрицу инциденций.

Рис. 1.60.

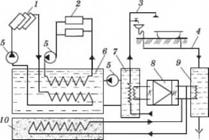Принципиальная схема си­стемы теплоснабжения с компрессионным тепловым насосом:

1 — солнечные коллекторы; 2 — си­стема отопления; 3 — горячее во­доснабжение; 4 — сточные воды; 5 — насосы; 6 — аккумулятор те­плоты; 7 — потребитель теплоты; 8 — тепловой насос; 9 — бак; 10 — теплообменник, установлен­ный в грунте; К — конденсатор; И — испаритель

Информационная схема, являющаяся основой для по­строения графа (рис. 1.61), отличается от принципиаль­ной схемы установки (рис. 1.60) подробным описанием теплового насоса и раскрытием всей совокупности тепло­обменных аппаратов, которое необходимо для более точно­го качественного описания процессов аккумулирования и передачи тепла.

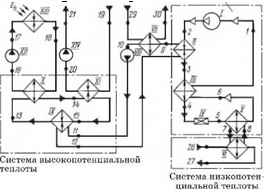
На рис. 1.62 представлен эксергетический потоковый граф рассматриваемой системы. Потоковый ЭПГ дополнен матрицей инциденций.

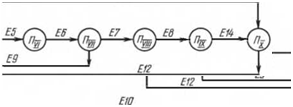
На рис. 1.61 и 1.62 приняты обозначения:

I — компрессор; II — конденсатор; III — регенератив­ный теплообменник; IV — дроссельный вентиль; V — испа­ритель; VI — теплообменник теплоты низкого потенциала; VII — теплообменник горячего водоснабжения; VIII, XII, XIV — насосы; IX — аккумулятор теплоты высокого потен­циала; X — теплообменник гелиосистемы; XI — теплообмен­ник отопительной системы; XIII — солнечный коллектор;

-» — эксерго-топологическии поток; => — поток эксергии вводимой в систему.

Для конкретной схемы ЭВМ рассчитывает необходи­мые данные и определяет значение эксергии в данной точке схемы, значение эксергетических потоков и потерь в элементах, а также эксергетический КПД г|эм системы в целом, сканируя по строкам матрицы инциденций. Ана­лизируя несколько вариантов схемных решений, можно определить оптимальное решение с точки зрения энергети­ческих потерь.

Значения удельной эксергии рабочего тела в узловых точках цикла

e. = h.-h — Т (8.-8 ). (1.268)

Эксергия, подводимая к системе (с учетом электромеха­нических КПД электродвигателей насосов и компрессора),

Явх =^+1(^/0- (1-269)

Потеря эксергии в главных элементах системы

Рис. 1.62.

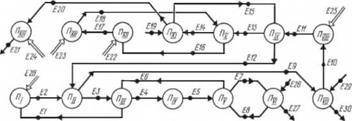Эксергетический потоковый граф и соответствующая ему матрица инциденций

П, = Elax + Y^ejmljGj.

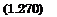
Потеря эксергии в прочих элементах системы

Эксергетический КПД системы

(1.272)

В этих формулах приняты обозначения: лг.. — ма­трица инциденций; Ne — эффективная мощность приво­да; G — расход; индексы: I — главные элементы системы; k — прочие элементы системы; Elp, Ehp, eyp ~ располагаемая эксергия элементов и системы в целом; i, j — коэффициен­ты влияния.

Представленная система уравнений (1.268)-(1.272) яв­ляется обобщенной математической моделью элементов системы и процессов, в них протекающих, и в совокуп­ности с балансовыми уравнениями и топологией схемы дает полную математическую модель системы, включая ее структуру.

10.1. ГЕЛИОУСТАНОВКИ С СЕЗОННЫМ АККУМУЛИРОВАНИЕМ ЭНЕРГИИ

Изучение сложной системы, каковой является энергос­берегающая установка, предполагает ее представление в виде модели, позволяющей выполнить анализ поведения системы при различных внешних воздействиях. Следует подчеркнуть, что свойства элементов могут изменяться в процессе действия системы в целом. Оптимизацию изучае­мых явлений нужно основывать на методе системного ана­лиза, который ориентирует исследования на раскрытие це­лостности объекта и взаимосвязи его основных элементов.

Решение этих задач невозможно без математического моделирования. Реализация соответствующих математи­ческих моделей на ЭВМ позволяет проводить анализ и по­иск наиболее обоснованных проектных решений.

При проведении системного анализа целесообразно об­ратиться к методам теории графов. Теоретико-графовые методы весьма результативны при анализе и синтезе си­стем энергосбережения [129,130].

Технологическую схему системы можно изобразить в виде потокового графа G(A, Г), где вершины — это элемен­ты схемы, а дуги — физические потоки (термодинамиче­ские параметры, потоки массы, теплоты, энергии) между элементами.

Для анализа энергосберегающих систем обратимся к параметрическому потоковому графу (ППГ) и к эксергети — ческому потоковому графу (ЭПГ).

Параметрический потоковый граф является топологи­ческой моделью системы. При построении ППГ создается информационная схема по технологической схеме и далее представляется в цифровой форме. Цифровым описанием выступает матрица инциденций, которая полностью отра­жает топологическую структуру информационной схемы и позволяет перенести эту структуру на язык алгебры или теории множеств.

Эксергетический потоковый граф учитывает не только параметры системы, но и потоки эксергии. Под ЭПГ следует понимать граф Е(А, Г) = Е(А, U), множество А = {аг а2,…. ак} вершин которого соответствует эксергетическим потерям в отдельных элементах системы, множество дуг U = {ир…. Uj}, k Ф I — распределению эксергетических потоков в системе;

Г — многозначное отображение множества А в себя. ЭПГ по аналогии с ППГ представляют в матричном виде.

На рис. 1.57 изображена схема системы теплохладос­набжения с адсорбционным термотрансформатором. Ис­точником энергии служит солнечное излучение. Данная схема предназначена для работы летом, поэтому термо­трансформатор используется в режиме кондиционирова­ния [131].

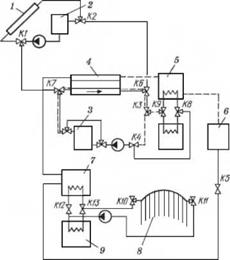Рис. 1.57.

Схема гелиоустановки с се­зонным аккумулированием энергии:

1 — солнечный коллектор; 2 — бак — аккумулятор солнечного конту­ра; 3 — бак-аккумулятор вторич­ного контура; 4 — теплообменник; 5, 7 — конденсаторы теплового насоса; 6 — расходный бак; 8 — се­зонный аккумулятор теплоты; 9 — испаритель

В ночное время суток хладагент из испарителя посту­пает в адсорбер. Теплота адсорбции отводится в грунто­вый аккумулятор-теплообменник. Часть вырабатываемо­го холода направляется потребителям, а остальная часть аккумулируется.

В дневное время используется холод, аккумулирован­ный в грунтовом теплообменнике.

Адсорбционные установки с твердым сорбционным по­глотителем имеют ряд преимуществ. Они не имеют движу­
щихся частей, не используют электроэнергию, просты в обслуживании.

В качестве сорбционных веществ используются цеоли­ты и силикагели. Более высокая сорбционная емкость до­стигается при применении в качестве адсорбента солей, на­пример, соединения СаС12 -2СН3ОН.

Основным термохимическим циклом СаС12—2СН3ОН в солнечной системе теплохладоснабжения будет следую­щий: солнечная энергия используется для разложения СаС12-2СН3ОН на СаС12 и пар при давлении около 300 мм рт. ст. Пар конденсируется при температуре 40 °С. Теплота конденсации может быть использована для нагрева воды, используемой на бытовые нужды. Этим завершается цикл генерации. Затем соль, отделенная от метанола, охлаж­дается и снова вступает в реакцию с паром. Жидкий ме­танол при испарении может охлаждаться до -25 °С. Обра­зующийся холод используется в системе хладоснабжения потребителей.

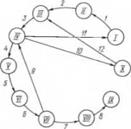На рис. 1.58 приведены параметрический потоковый граф анализируемой схемы и соответствующая матрица инциденций.

Эксергетический потоковый граф и матрица инциден — ций схемы, показанной на рис. 1.57, изображены на рис. 1.59.

Сканируя по матрицам инциденций для ППГ и опреде­ляя булеву переменную на своем пути, ЭВМ рассчитывает все необходимые данные и находит значения параметров в данной узловой точке графа, значения тепловых и массовых потоков, условия оптимальной топологии схемы. Анало­гично по матрице ЭПГ ЭВМ вычисляет значения эксергии, эксергетических потоков и, следовательно, определяет сте­пень энергетического совершенства системы.

Математическая модель анализируемой системы тепло­снабжения или отдельных ее элементов может быть пред­ставлена в виде функционального оператора

где і — коды элементов (1, 2,п); Yt — вектор выходных па­раметров і-го элемента; Фг — вектор параметров функцио­нальных характеристик системы; дГ, , /£~ — нелинейные

вектор-функции i-ro элемента; X] — вектор входных вну­тренних параметров i-ro элемента; zTt — вектор режимных параметров і-го элемента; К — вектор конструктивных параметров і-го элемента: ТГ — топология подключения і-го элемента; Z — нелинейная функция критерия эффек­тивности; |/ — вид уравнения состояния; р, Т, h, s, р — со­ответственно давление, температура, энтальпия, энтропия, плотность рабочего тела; £, — параметр фазового превраще­ния в термотрансформаторе, для компрессионного тепло­вого насоса £ = 1.

Топология подключения і-го элемента определяет его место в схеме и его математическое описание по і-му ходу.

Уравнение баланса расходов і-го элемента:

= (1.259)

і=1

Уравнение баланса компонента для смеси рабочего тела теплового насоса:

Z Gjm^O. (1.260)

/=і

Уравнение баланса энергии і-го элемента с учетом топо­логии схемы:

+Nt=0. (1.261)

і=і

где Nt — внешняя энергетическая нагрузка на і-й элемент.

Уравнение гидравлического баланса потока в і-м элементе

^Р^ + Щ = 0. (1.262)

/=і

Изменения энтальпии потока в і — м элементе

j=h

^А/77іу + ДАу = 0. (1.263)

/=і

В этих уравнениях приняты обозначения: G — расход ра­бочего тела; APj — потери давления в данном элементе; ДЛу — изменение энтальпии раствора; пг. у — матрица инциденций.

Структурный анализ и оптимизация исходной много­контурной схемы основывается на следующем. Схемы представлены в виде параметрических графов, содержа­щих р разнопараметрических дуг S = (Sv S2, …, S ) и и простых контуров (Lj, L2, …, Lu). Необходимо в исходном параметрическом потоковом графе определить множе­ство особых дуг S* = (S1, S2, …. Sp), S* cz S, S* = p, p й и с минимальной суммой параметричностей. При этом не существует никакого другого подмножества R a S, R Ф S*, обладающего тем же свойством. Минимальная сумма пара­метричностей определяется соотношением р = min.

С энергетической точки зрения оптимум решения опре­деляется условием минимальных потерь эксергии:

^ПА=тіп. (1.264)

Изложим основные принципы синтеза энергосберегаю­щих систем.

Анализ схем энергосберегающих систем позволил уста­новить дискретность изменения параметров, структуру схемы и состав оборудования, нелинейность взаимосвязей между ними, нелинейность целевой функций и ограниче­нии. Поэтому данная задача является нелинейной задачей дискретной оптимизации. В качестве целевой функции могут быть приняты различные характеристики системы: технологические, энергетические, экономические и др. Будем исходить из того, что критерием оптимизации явля­ется энергетический показатель.

Пусть дан граф G(X, Г) = G(X, U), где X = {х.}, і = 1, 2, …, п — множество его вершин, соответствующих некоторым численным значениям граничных и промежуточных зна­чений параметра. Задача заключается в том, чтобы найти кратчайший путь (по минимуму суммарного веса входя­щих в него дуг), т. е. минимизировать функцию

(1-265)

і і

для всех і и у, принадлежащих сети, і є х, у є х, і = 1, 2,…, п; j = 1, 2, …, п — номера вершин; EL. — вес дуги і, /, т. е. за­траты первичной эксергии, соответствующие данной дуге;

1, если дуга i, j входит в рассматриваемый путь; О, в противном случае.

Граничные условия

1, k~s (источник), s-x0; О, для всех остальных хк ; -1, для k~t (сток), t~xn.

Сформулированная задача — это комбинаторная за­дача целочисленного дискретного программирования с булевыми переменными. Множество вершин X = {xj, i = l,2,…, п, формируется эвристически, исходя из опыта программирования.

Аналогично решается задача, если целевой функцией является один из экономических показателей.

Один из результативных методов оптимально­го синтеза энергосберегающих систем основывается на декомпозиционно-поисковом принципе. При этом возмож­ны несколько видов декомпозиции. Наибольший интерес представляет перспективно-отсекающая декомпозиция. Суть ее заключается в поиске оптимального решения Р* в подмножестве допустимых или перспективных решений {22}, т. е. Р*є {Е} с= {Р}, где {Р} — множество всех решений.