In order to evaluate the system behaviour under different draw off volumes and to determine the maximum usable hot water over a whole year, several simulations have been carried with a collector tilt angle of 42° under the climatic conditions of Rome. It has been assumed that hot water is only needed in the evening in between 6.00 — 8.00 pm. The system is included into an existing hot water system consisting e. g. of a gas boiler for hot water and room heating or a simple electronic hot water boiler.

An automatic tempering valve at the hot water outlet of the storage prevents the users from scalding themselves. A selector valve automatically takes the hot water from the backup heating if the hot water temperature turns below 45°C. Figure 6 shows a schematic drawing of the system.

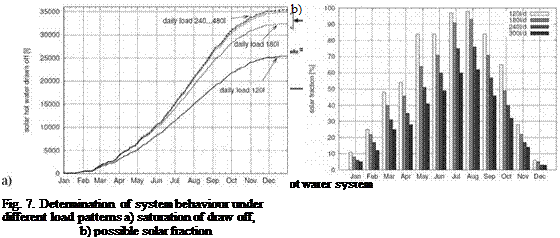
The daily draw off pattern was varied in the range of 120l/d.480l/d. As a first result of these variations it can be seen that the hot water draw off out of the 180l storage is limited to about 35,000l/a respectively the draw off gets saturated at about 240l/d, because of the climatic

conditions. With a draw off profile of only 120l/d, an annual solar hot water fraction of about 66% can be achieved. In terms of saved energy this equals a reduction of about 95l of fuel oil. With a hot water demand of 180l/d, it is still possible to cover nearly 50% of the annual hot water demand or an equivalent of 125l of fuel oil with only one collector of about 2m2 and a 180l storage tank.

4. Conclusion

The paper presents the implementation of a double mantle heat exchanger into the simulation environment CARNOT and first simulation results calculated with the new storage type.

The developed double mantle heat exchanger storage is based on the TRNSYS double mantle heat exchanger storage but was enhanced by the possibility of including user settable material and geometric data.

Concerning the system simulation, some “to dos” remain, like the validation of a modified “thermosiphonic pump”, which is able to calculate the fact of reverse thermosiphoning e. g. at night. In order to improve the system and to identify other main influencing variables, further simulation runs have to be carried out, e. g. with regard to overheating.

References

[1] S. Gurtner, F.-D. Treikauskas, W. Zorner: „Prufstand fur Thermosiphonanlage am Kompetenzzentrum Solartechnik an der Fachhochschule Ingolstadt“, 16. Symposium Thermische Solarenergie, Kloster Banz / Staffelstein (Germany), May 2006, p. 118 — 122.

[2] S. Brandmayr, W. Zorner: “Thermosiphon Systems: Market, State-of-the-Art and Trends“, 3rd European Solar Thermal Energy Conference (estec2007), Freiburg (Germany), June 2007, p. 182 — 188.

[3] N. N.: “Matlab/Simulink user manuals”, The Mathworks Inc., http://www. mathworks. com, Natick (USA), 2002.

[4] B. Hafner, J. Plettner, C. Wemhoner: “CARNOT Blockset: Conventional And Renewable eNergy systems OpTimization Blockset — User’s Guide”, Solar-Institut Julich, Aachen University of Applied Sciences (Germany), 1999.

[5] A. Carillo Andres, J. M. Cejudo Lopez: “TRNSYS model of a thermosiphon solar domestic water heater with a horizontal store and mantle heat exchanger”, Solar Energy, Vol. 72/2 (2002), p. 89 — 98.

[6] G. L. Morrison, D. B.J. Ranatunga: “Thermosyphon circulation in solar collectors”, Solar Energy, Vol. 24 (1980), p. 191 — 198.

O. Kusyy*, K. Vajen, U. Jordan

Kassel University, Institute of Thermal Engineering, Kassel, Germany
* Corresponding Author, solar@uni-kassel. de
Abstract

In this paper the application of sensitivity analysis to the investigation of solar water heating systems is considered. Two global sensitivity analysis methods are described and applied to different solar heating systems. The first one is the Morris method that only ranks parameters by importance and the second one is the Fourier amplitude sensitivity test (FAST) that quantifies the influence of the parameters on the target functions. The both methods were implemented into the GenOpt (Generic Optimization) software and coupled with the TRNSYS simulation program.

Keywords: Sensitivity analysis, Fourier amplitude sensitivity test, Morris method

1. Introduction

In recent years, many middle to large solar heating systems were installed all around Europe and especially in Germany. A proper design of such systems is decisive for their functionality. Underdimensioning or poor selection of design parameters as well as the control strategy could lead to an overall poor efficiency of the systems. During the designing process, the advanced numerical optimization methods should be used in order to find the optimal parameter values that provide the best efficiency of the system. Considering that the target functions depend on a high number of optimization parameters and that the global optimization algorithms require large number of system simulations, the task of optimization turns to be very computationally expensive. In order to decrease the number of optimization parameters and, thus, make the optimization faster, the sensitivity analysis of parameters could be used prior to optimization. Only the most influential parameters are then selected for optimization. Another straightforward application of the sensitivity analysis is analysis of uncertainties, that is, how uncertainties in parameters influence the uncertainty of the target function. Here two sensitivity analysis methods are described and applied to the analysis of two solar heating systems. For the first system the influence of the operation parameters on the cost function is investigated by the qualitative Morris method. A more comprehensive Fourier amplitude sensitivity test is applied to the investigation of the influence of the design parameters on the solar fractional savings function of the second system. In this paper only the exemplary examples of applications of the both methods are considered. The methodological application of the methods is planned but not yet realized.

In general the output of the solar cycle is calculated using the formula:

Q = Q u — CL — Q

out abs heat pipe

The solar irradiation absorbed by the collector is:

Qabs = Edir ‘ П ‘ Aaperture ‘ F dir (0) + Ediffuse ‘ П ‘ Aaperture ‘ F diffuse

The calculation of the direct irradiance EdlI and the diffuse irradiance Ediff on the collector is based on the relevant meteorological values on the horizontal plane. Shading of the horizon can also be considered in these calculations.

The angle of incidence on the collector is [2]:

0 = arccos(-sin^C cosys cos(aS — aC) + cosyC sinYS)

For vacuum tube collectors the angle of incidence 0 is divided into a longitudinal 0 and a transversal angle of incidence 0t referring to the collector axis According to [3] the following formulas can be used:

0 =|rC + arctan(tan(90°-ys) • cos(aS — aC)) and

arctan(cosfS • sin(aS — aC))
cos#

The incidence angle modifier for the direct irradiance IAMdir of the vacuum tube collector is now defined by a longitudinal share IAMdirl and a transversal share IAMdir, t :

IAMdh(0) = IAM„„(А,)• IAMdlJ01).

The angles aS and yS describe the position of the sun according to DIN 5034 (aS: 0°=N, 90°=E, 180°=S, 270°=W. yS: 0°=horizontal, 90°=vertical) and aC and yC the orientation of the collector axis (aC: 0°=S, 90°=W, 180°=N, 270°=E. yC: 0°=horizontal, 90°=vertical).

The collector heat losses are calculated with the following formula:

Q heat = П • Aaperture •(k! •AT + k2 •AT2 )

The pipe losses are defined using the mean collector temperature Sc and the ambient temperature Sa as follows:

a pip,=V-te — sa )+k2′( — 20 °c)

with

and

Typically the calculation is done for a whole year including also the night hours without heat input to the collectors. During these hours the whole system cools down and in the morning the whole system has to be heated up to design temperature. For this calculation the heat capacity of the pipes, the heat transfer fluid and the collectors are considered. Collector parameters are input values and stored in the collector database. They may be obtained from collector manufacturers or from [4].

The local management is regarded in 4 distinct blocks:

Photovoltaic systems installed in the municipality;

Identification of a determined model and manufacturer for each component;

Identification of a determined model and manufacturer of photovoltaic modules;

Operational situation of all the components of the installed photovoltaic systems;

Identification of the nearest training and maintenance center.

(d)

Figure 3 — Macro-spatial functionalities of the SIGA-SOL, PV management by type of application and

filtering of some specific aspects

(a)

Figure 4 — Macro-spatial functionalities of the SIGA-SOL, PV management, photovoltaic system
components and a more detailed filtering by a menu

Fig. 6 (a) shows the photovoltaic systems installed in the municipality of Ibimirim in the state of Pernambuco and in (b) which are the models of PV modules that were used in the systems. Fig. 7 (a) shows the operational state of PV system components installed in Pernambuco and in (b) the nearest maintenance centers.

Janybek Orozaliev[3] [4]*, Christian Budig1, Klaus Vajen1, Elimar Frank1#,
Ruslan Botpaev[5], Alaibek Obozov2

1 Kassel University, Institute of Thermal Energy Engineering, Kassel (Germany)

2 Kyrgyz State Technical University, Department for Renewable Energies, Bishkek (Kyrgyzstan)
Corresponding Author, www. solar. uni-kassel. de

Abstract

A fin-and-tube heat exchanger model is presented in this paper. It uses empirical heat transfer and flow friction correlations identified in the literature. The model structure, its range of validity and accuracy are described in detail. Additionally, the model performance is compared with the producer design software GPC.

1. Introduction

Fin-and-tube heat exchangers are widely used in industry and residential air conditioning for heat transfer between a liquid and a gas, e. g. for water cooling, air cooling or heating. In the context of a research project in Bishkek (Kyrgyzstan) such a heat exchanger is applied in a multicomponent solar thermal system [1] to heat up cold water for a district heating net by using the enthalpy of the ambient air. The ambient air is also preheated with an unglazed transpired air collector before going through a heat exchanger.

In practice, the heat exchanger geometry is selected by designers relying on their personal experience and some recommendations1. If the heat capacity rate ratio of liquid to air is not defined by the application, a typical value (e. g. 2) is applied. This procedure works well for standard applications. But for non-standard applications with different boundary conditions (e. g. low electricity prices) as described above, there are more detailed investigations necessary. In order to optimize the heat exchanger configuration for this application, a detailed heat exchanger model was developed, which is presented in this paper.

1.1. Concept

The concept of the new implemented structure level in SIMULATION STUDIO is based on the aim of obtaining a well structured graphical representation of the complete model on the one hand and a high level of modularity and flexibility on the other hand. This is achieved by dividing a model in several subsystems, which can be connected and replaced easily. In this way, modularity is given not only on component but also on subsystem level. A new feature realized within the subsystem approach is the possibility of removing and transferring subsystems without deleting or reconfiguring any visual connections in SIMULATION STUDIO. Fig. 2 shows a sketch of the new subsystem based structure level.

1.2. Subsystems

A subsystem is a collection of several components which are connected to each other in the common TRNSYS way. In solar thermal systems the subsystems are conform to the several loops in such a system, e. g. collector loop. Direct connections between components from different subsystems do not occur anymore. Instead of these connections the subsystems are connected via uniform interfaces. This gives the edge of avoiding many overlapping links in the graphical representation. Parameters that are used by the components within the subsystems are defined in separate EQUATION blocks belonging to the respective subsystem. As an example Fig. 3 shows the subsystem of a possible collector loop.

T. Matuska*, J. Metzger and V. Zmrhal

Czech Technical University, Faculty of Mechanical Engineering, Department of Environmental Engineering,

Technicka 4, 166 07 Prague 6, Czech Republic

* Corresponding Author, tomas. matuska@fs. cvut. cz

Abstract

Mathematical model and design software tool KOLEKTOR 2.2 with user-friendly interface for detailed modelling of solar thermal flat-plate collectors is presented. Mathematical model is based on internal and external energy balance of the absorber solved in iteration loops to determine the temperature distribution and heat transfer coefficients in main parts of solar collector. Mathematical model has been validated with experimentally obtained data for different solar flat-plate collector concepts (low and high performance atmospheric collectors, evacuated collector). The software tool KOLEKTOR 2.2 is applicable especially for design and virtual prototyping of new solar flat-plate collectors resulting in efficiency curve determination, for parametric analyses to obtain information on different parameters influence on collector performance and especially for investigation of thermal performance of advanced solar collectors (building integrated, evacuated collectors, etc.).

Keywords: solar collector, evacuated collector, performance modelling, experimental validation

1. Introduction

Computer modelling of solar thermal collectors is a principle approach for testing of new construction concepts and improvements in the development and design stage for developers and manufacturers. Virtual prototyping of solar collectors can save the investments into number of prototypes and foreseen the collector performance in advance. Analyses of individual construction parts and details parameters impact on the collector performance is needed to make decision on efficient solar collector concepts for given application, operation and climatic conditions with respect to economic parameters of construction.

A mathematical model is always a simplification of reality to certain extent. Too complex mathematical models and numerical programs require huge amount of computer time for calculations, too simplified models don’t take important influences of detailed collector parameters into account and result in considerable uncertainty in calculation. To find a good compromise between simplicity of the model and its accuracy is crucial for development of any design and simulation tool.

Although the theory of flat-plate solar collectors is well established and can be found in basic literature [1-3], there is a lack of user-friendly design programs for solar collector performance modelling considering the detailed geometrical and physical parameters of collector. Number of authors evolved simplified analytical models considering temperature independent solar collector overall heat loss coefficient (linear dependence of efficiency), neglecting the absorber temperature distribution or temperature difference between absorber surface and heat transfer fluid. Such

models are not comparable with physical experiments and cannot predict the real performance behaviour and evaluate efficiency characteristics of solar collectors.

Theoretical model of solar collector has been introduced in TRNSYS Type 73 [4] but with simplified calculation of collector heat loss coefficient U insufficient to cover wide range of parameters affecting the collector heat loss. More theoretical model with number of detailed input parameters and calculation of heat transfer coefficients in the individual parts of collector (in air gaps, inside pipes, at outer surfaces) has been evolved as a Type 103 [5].

A design program CoDePro [6] for energy performance calculation of solar flat-plate collectors has been developed with the Energy Equation Solver. It allows a very detailed specification of collector geometrical and material parameters. It covers large segment of solar collectors (unglazed, single and double glazed) and evaluates also optical properties of collector, e. g. incident angle modifier. On the other hand, the features of CoDePro program, analogous to TRNSYS Type 103, don’t allow energy performance modelling of advanced solar collectors, e. g. collectors integrated into building envelope, evacuated flat-plate collectors or solar collector with glazing made of transparent structures.

The presented model and design tool KOLEKTOR 2.2 has been developed to overcome the drawbacks of previous models. KOLEKTOR 2.2 is based on detailed calculation of heat transfer from the collector absorber to ambient and from the collector absorber to heat transfer fluid. The advantage of the design tool is its universality to wide-range of solar flat-plate collectors stock from evacuated to atmospheric, separately or building integrated, covered with different types of glazing (single glazing or transparent insulation structures), etc.

The analysis will deal with a theoretical building (used in the IEA-ECBCS annex 48 project — Heating Pumping and Reversible Air Conditioning -) fully defined by P. Stabat [3] . It is a twelve identical floors, 15000 m2 building with average 1000 persons occupancy. Representative existing European office building parameters are used [3] . Set points and ventilation rate are defined in table 2. . U value [W/(m2 K)] for external walls is 0.8, 0.4 for roof and 2.95 for glazing.

In TRNSYS, only one floor with 5 thermal zones is simulated, there is no heat transfer considered between floors.

T. Kusunoki1* and M. Udagawa1

1Kogakuin University, 1-24-2 Nishi-Shinjuku, Shinjuku-ku, Tokyo, 163-8677, JAPAN
Corresponding Author, dd08002@ns. kogakuin. ac. jp

Abstract

As the performance of solar hot water heating system is strongly influenced by heat load, this study is focused on the followings.

1) Usually the simulation of the solar hot water heating system is carried out with 1 hour time increment. However, the domestic hot water demand varies in very short time. In this study, the simulation was carried out for considering the suitable simulation time increments in solar hot water heating systems. As a result, it was found that 10 minutes is the suitable time increment for the simulation of the solar hot water heating system.

2) Using the time increment of 10 minutes, the simulation for 42 combinations of collector tilt angle and azimuth for five cities in Japan was carried out. As a result, it was found that the difference in the performance of solar hot water heating systems was within 15% from the best performance with the combination of the tilt angle from10 to 60 degrees and azimuth within 45 degrees from the south in Tokyo. The similar results were obtained for the combination of the tilt angle and azimuth in other four cities. The simulation result showed that the solar contribution for DHW heating load in Sapporo, Morioka, Sendai, Tokyo and Kagoshima were 44 %, 46 %, 51 %, 57 % and 66 %, respectively. The difference is caused by the DHW heating load which is strongly influenced by the city water temperature.

Keywords: Solar DHW System, Simulation Time Increments, Tilt Angle, Azimuth

1. Introduction

More than 35% of the purchased energy consumption is used for domestic hot water (DHW) heating in the Japanese housing sector. Therefore, it is important to reduce the energy consumption used for the hot water heating. Reduction of the energy consumption by solar DHW heating system is expected in the housing sector.

Solar DHW heating systems are affected by the DHW use profile as well as the solar radiation on collector. As the DHW use varies in very short time, the simulation of the solar DHW heating systems needs to consider for suitable time increments in the simulation. In this study, the time increment in the simulation of the solar DHW heating systems to reflect the detailed hot water use profile was examined first.

The overall solar system performance was also studied to find the allowable collector tilt angle and azimuth in designing the solar DHW heating system. In addition, the total performance of the solar DHW system is compared for five cities in Japan.

The CFD analysis of the ICS-SWH was undertaken in order to improve the four fin ICS-SWH performance by optimising the fin spacing. Prior to simulation issues regarding the parameters influencing fin optimisation need to be determined, constrains need to be stated, heat transfer parameters need to be outlined and the type of CFD analysis need to be established.

Fin material, length and thickness and the number of fins in the ICS-SWH are the four main parameters to be outlined when analysing fin optimisation. The material thermal conductivity is an intrinsic parameter for effective ICS-SWH. The low density, high thermal conductivity and recyclable properties of aluminium highlighted this material as an effective choice. The fin length was fixed at the maximum length of 800mm. Fins are used to increase the heat transfer from the heated surface by increasing the effective surface area. The effectiveness of the fin is enhanced by increasing the ratio of the perimeter to the cross-sectional [7] therefore the use of thin, but closely spaced fins is preferred, with the provision that the fin gap is not reduced to a value where flow between the fins is severely impeded, thereby reducing the convection coefficient. The present study thus looks at the increase in performance of the ICS-SWH by increasing the number of fins.

Three main constraints affect this study; cost, volume (50litre tank size) and manufacturing ability which need to be borne in mind when choosing the new design.

Three main heat transfer parameters influence the ICS-SWH performance and can be recapitulated as: the shape of fins, the angle of inclination of the heater, and time of exposure to incident solar radiation. Due to manufacturing constraints, simple rectangular shapes of fins were considered. A 45 degree inclination angle and a 300W/m2 heat flux were taken as the reference conditions [6].

Finally, the type of CFD analysis, 2D or 3D, is an important parameter to consider. Previous studies [9] outlined that 2D analysis was sufficient for a good analysis of the system. However, 2D analysis would only suffice for a horizontal inclination of the heater. For any angle above zero a gradient exists in the longitudinal direction making a 2D analysis insufficient. Hence, based on a 45 degree inclination of the collector, a 3D analysis was undertaken. As the Quiescent fluid is unavailable in CFD simulation, the process was assumed transient.