Meteorological data can be generated with Meteonorm using a database with long term monthly average measurement data from different stations. In the recent software versions there are more than 7000 meteorological stations worldwide available. If no meteorological station is available in the database for a desired site, meteorological data will be interpolated based on the data of the nearest stations. The accuracy of the generated data depends on the accuracy of measurements of used stations in the database, the distance to the next stations and the interpolation method.

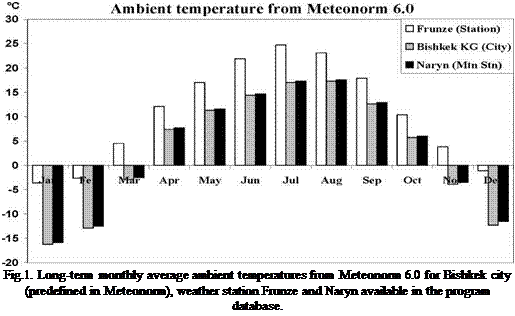A density of weather stations in the program database is relatively low for Central Asia compared to Europe. In total, about 100 stations are available in the program database (5.1 and 6.0) for Central Asia with data for ambient temperature, humidity, velocity and wind direction, precipitation and only 3 stations with solar radiation data. The mentioned station Frunze in Bishkek is available in the program database, but without solar radiation data. The nearest database station to Bishkek with solar radiation data is about 600 km away in Tashkent, Uzbekistan. Unlike previous versions, Meteonorm 6.0 uses satellite-derived solar radiation data additionally to the weather stations for interpolation of solar radiation.

Bishkek city is already defined in Meteonorm 5.1 and 6.0 but with a wrong altitude of 2111 m instead of 760 m. This leads to significantly lower ambient temperatures compared to the measure

values at the weather station Frunze (Fig 1). Because of the wrong altitude, ambient temperature for Bishkek was obviously interpolated by Meteonorm using data from a station Naryn (about 300 km away) with a similar altitude of 2041 m. Thus, it is necessary for further investigations to define Bishkek in Meteonorm manually as a new site with the correct coordinates.

The extraterrestrial solar radiation on the horizontal surface is the function of Latitude of the location. As the solar radiation passes through the earth’s atmosphere, it is further modified by the processes of scattering and absorption due to the presence of the cloud and atmospheric particles. Hence, the solar radiation incident on the horizontal surface is to some extent locality-dependent and less than the extraterrestrial irradiation.

Several climatic parameters have been used to develop empirical relations to predict the solar radiation incident on the horizontal surface. Among these existing correlations, the Angstrom-Prescott type regression equation related monthly average daily radiation to clear-day radiation at the location in question and average fraction of possible sunshine hours is considered to widely accept by the scholars [9]:

h . S

= a+b (1)

H о ^

The Equation (1) has been proved to accurately predict the global solar radiation.

H : the monthly average daily global radiation on the horizontal surface(MJm-2 day-1)

H0: the monthly average daily extraterrestrial radiation on the horizontal surface (MJm-2day-1)

S : the monthly average daily number of hours bright sunshine

S0 : the monthly average daily maximum number of hours bright sunshine a, b : the regression constants to be determined

The extraterrestrial solar radiation [9] on a horizontal surface is determined by following equation.

24*3600 . 0 ■ п.

H0 = 10 f (cos л cos о sin a>s + a>s sin Asm0) (2)

n 180

Where I0 =1367 Wm 2 is the solar constant, Л is the latitude of the location, 0 is the declination angle.

n

and f = 1 + 0.033cos(360 ) (3)

365

Where n is the Julian number (for example Jan 1st is the number 1)

(4)

And a>s is the sunset hours angle given as

cos = cos 1 (- tan Л tan 0) The maximum possible sunshine duration

S 2

s0 =

0 15 s

H>, So in the equation are obtained from the equation(2) and (6).The regression coefficient a

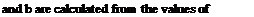H S

and. The values of the monthly average daily H 0 S0

global radiation and the average number of sunshine duration are obtained from daily measurements for a period of ten years.

The regression coefficient (a, b) can be computed by the following formulas:

b

(7)

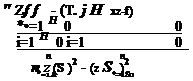1 H bA S

a = z — z

n і=1 H 0 n і=1 S0

Where n is the number of measured data points.

The NWP uncertainties of the rainfall forecast is based on non-stationary, nonlinear and dynamic effects as stated by Todini [18]. As the solar radiation forecast is also a function of the cloud cover, it is probably subjected to the same underlying effects. For non-stationary signals the short-time Fourier transform, also named as Fast Fourier Transform (FFT) has the disadvantage that the information concerning the frequency content at a specific time interval can only be obtained with limited uncertainty. By the Heisenberg uncertainty theorem the method increases its uncertainty for the frequency, if the width of analyzing time window is small, and in the time location of a

particular shape if the windows width is large [19]. A high resolution in time and frequency is obtained by the wavelet convolution, also referred as mathematical microscope [20], where the analyzing time window with is variable in a single transformation. With digital computers the Discrete Wavelet Transform (DWT), has the advantage to reconstruct the decomposed signal with lower uncertainties than the Continuous Wavelet Transformation (CWT) [19]. Also the amount of convolutions is reduced with the DWT which increase the transform speed. This transform is based on the members of a family of functions [20]. One has to begin with the selection of the family of wavelets, e. g. the bi-orthogonal wavelet family, and one of the mother wavelets within the selected family. While the orthogonal DWT uses the inverse filters for the reconstruction of the signal, the bi-orthogonal transform introduced by Cohen [21] permits the utilization of distinct filters for the decomposition of the signal and its reconstruction (Souza [22] citing [21]) in order to obtain symmetric wavelet functions. The mother wavelet function determines the order and specifies the time window or support length of the convolution at the first time scale (m = 1). Also each mother wavelet has its own function shape and degrees of freedom [19]. A TDW transform is accomplished at different time scales (m = 1 … mx), using different functions, named by the members of a family, which are all specifically related to the mother wavelet function. If at a specific time location the signal shape is similar to the wavelet shape, one obtains high wavelet convolution coefficients. At each of the m time scales the signal is convoluted by the DWT with distinct wavelet functions. The daughter wavelet functions ym, n(t) (eqn.1) are equal to the expanded and translated mother wavelet functions у [19].

ym, n(t) = 2-m/2 y( 2-m t — n) ; m, n є Z; t є ^ (1)

Where m defines the scaling or expansion of the mother wavelet and n defines the translation of у, relatively to the time t of the time series values from the signal to be analyzed. Due to the expansion, the convolution support lengths are increased by the factor two from scale m to m+1. For the DWT, the wavelet convolutions are obtained by a filter bank of Finite Impulse Response (FIR) digital filters [19] (Figure 1a). The filter bank separate by low and high pass filters the signal to be analyzed in signals with distinct frequency bands. The mother wavelet (Figure 1a — first bk filter) represents the FIR high pass which separates the highest frequencies appearing within the bandwidth of (SL -1 … ГО). SL is the support length of the mother wavelet. The low pass filters ck, also named as scaling function, represent on its output the signal with the complementary low frequency band until to zero frequency. At m = 1, e. g. the complementary frequency bandwidth is (0 … SL-1) and for m = 2 its frequency content decrease to (0 .. .(2SL)’1). The frequency band of the high pass filter at this scale is ((2 SL)-1… SL-1) and from scale m to (m+1) its band width is reduced by the factor two. Where in the Fourier transform the frequency bins are hold constant, in DWT the energy is hold constant to obtain nearly complete reconstruction of the original time series signal. The signal details and approximations at distinct time scales or filter bands are obtained by the bk and ck filters (Figure 1a). The last scaling function is also known as father scaling function [20].

The downsampling function (2f) after each filter reduces the vector length by two, avoiding a redundant representation of the decomposed signal and due to the upsampling (2t) the signal is reconstructed to its original vector length. The decomposed signal can be represented by the wavelet and scaling coefficient vectors T(m, n) and S(m, n) (Figure 1), or by equal length partially reconstructed sub-signals. If during the reconstruction of the original signal, utilizing the inverse filter bank (Figure 1 b), only one of these vectors is supplied to its input, the signal which corresponds to the supplied vector, is reconstructed to the length of the original time series. This wavelet transform is also referred as Non Decimated Wavelet Transform (NDWT), or a trous WT and its partially reconstructed signal vectors are here named as sub-signals. Beside the

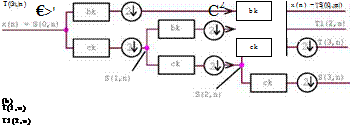reconstruction based on the wavelet and scaling coefficients (Figure 1 b), with the NDWT one can reconstruct the original signal by the sum of the complete sub-signal set.

Cf(1,k)

Cf(2,k)

Figure 1 — Wavelet digital filter bank for the decomposition of a signal (a) and its reconstruction (b), where ( 2i ) stands for the downsampling process and ( 2t ) stands for the upsampling process

In the residual kriging procedure, instead of kriging Z (x) directly, a regression analysis is first carried out between Z (x) and some external variables. Then, the residuals r (x) and the spatial field Z * (x) can be estimated for each point x generated from the regression results. The new variable r (x) retains the spatial variability of Z (x), but some of the variability has been removed, as a result of external information used in the regression model.

After this analysis, a kriging procedure is used for the residuals r(x) . As a results, a map of r(x), representing the corrections to apply to the regression model, is obtained. The final estimates Z(x) are obtained by combining both Z * (x) and r(x) estimates separately on the kriging grid:

Z( x) = Z * (x) + r( x).

2. APPLICATION

A. Kemper, E. Lorenz, A. Hammer and D. Heinemann

Department of Energy and Semiconductor Research, Faculty V — Institute of Physics Oldenburg University, D-26111 Oldenburg, Germany Corresponding Author, axel. kemper@uni-oldenburg. de

Abstract

We present a method to derive the direct normal irradiance DNI from MSG data. For this we apply the Heliosat method to extract cloudiness from the satellite images. Clouds are causing high fluctuations in the DNI. A new model for the direct fraction of the irradiance is introduced to calculate DNI. The clear sky irradiance is mainly determined by the aerosol optical depth (AOD) and water vapour content, which are taken from suitable climatologies. The accuracy of satellite derived DNI data is analyzed here for Spanish sites.

1. Introduction

Measurements of the direct normal irradiance DNI are needed for the planning of a solar thermal power plant at a given site. Direct solar irradiance is highly variable in space and time. As ground measurements are expensive, such data are rare.

Meteorological satellites operationally scan the Earth’s surface and clouds. So we can derive the direct normal irradiance from their data with a good spatial and temporal coverage. Since 2004, the satellites of the new generation MSG provide images of Africa and Europe every 15 minutes with a spatial resolution of approximately 1 km x 1 km at sub-satellite point.

In this document, we first present a method to derive the direct normal irradiance DNI from MSG data. A new model for the direct fraction of irradiance is used in combination with the Heliosat method applied to MSG data. In a second step we analyse the accuracy of the satellite derived DNI with ground measurements of six Spanish sites.

In this study, we used one year (2005) of global irradiance measurements from 14 stations located in the Sierra Nevada Natural Park, in Hueneja (Granada, Spain). The stations are equipped with LICOR 200-SZ pyranometers, with a sample frequency of 2.5 minutes. In addition, we utilized a DTM with 100 m resolution containing the area where the stations are located, and provided by the local government Junta de Andalucia. Table 1 shows the characteristics of the stations and Figure 1 shows their location inside the studied area.

1.1. Meteosat Images

The satellite images used in this work cover a period of time convergent with the information from the pyrometers. These are images of high resolution and correspond to the visible channel of the satellite METEOSAT-7 (HRI-VIS) and they have been registered by the PDUS (Primary Data User Station) station located in the Department of Renewable Energies of the CIEMAT (DER-CIEMAT).

definition that constitutes the principal subsystem of the METEOSAT. In case of the images corresponding to the visible channel the field of instantaneous vision, according to the angular amplitude of the sensor and of the orbital distance of the satellite, is 2.5 km in the nadir or point of the subsatellite (latitude=0°, longitude= 0 °). Due to the terrestrial curvature this magnitude increases according to the distance to the point of the subsatellite (for the studied zone approximately 3.5 km).

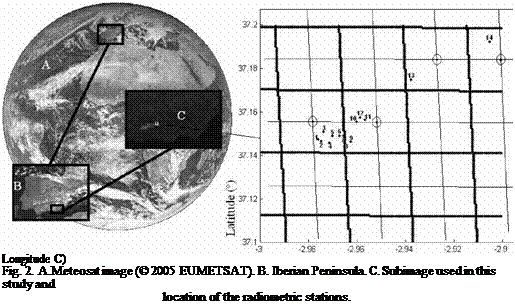Every pixel of the image has a value of brilliance, registered by the satellite, on the grey scale of 0-255 (8 bits). The 14 stations are located in four different pixels of the image, as shown in Figure 2.