The NWP uncertainties of the rainfall forecast is based on non-stationary, nonlinear and dynamic effects as stated by Todini [18]. As the solar radiation forecast is also a function of the cloud cover, it is probably subjected to the same underlying effects. For non-stationary signals the short-time Fourier transform, also named as Fast Fourier Transform (FFT) has the disadvantage that the information concerning the frequency content at a specific time interval can only be obtained with limited uncertainty. By the Heisenberg uncertainty theorem the method increases its uncertainty for the frequency, if the width of analyzing time window is small, and in the time location of a

particular shape if the windows width is large [19]. A high resolution in time and frequency is obtained by the wavelet convolution, also referred as mathematical microscope [20], where the analyzing time window with is variable in a single transformation. With digital computers the Discrete Wavelet Transform (DWT), has the advantage to reconstruct the decomposed signal with lower uncertainties than the Continuous Wavelet Transformation (CWT) [19]. Also the amount of convolutions is reduced with the DWT which increase the transform speed. This transform is based on the members of a family of functions [20]. One has to begin with the selection of the family of wavelets, e. g. the bi-orthogonal wavelet family, and one of the mother wavelets within the selected family. While the orthogonal DWT uses the inverse filters for the reconstruction of the signal, the bi-orthogonal transform introduced by Cohen [21] permits the utilization of distinct filters for the decomposition of the signal and its reconstruction (Souza [22] citing [21]) in order to obtain symmetric wavelet functions. The mother wavelet function determines the order and specifies the time window or support length of the convolution at the first time scale (m = 1). Also each mother wavelet has its own function shape and degrees of freedom [19]. A TDW transform is accomplished at different time scales (m = 1 … mx), using different functions, named by the members of a family, which are all specifically related to the mother wavelet function. If at a specific time location the signal shape is similar to the wavelet shape, one obtains high wavelet convolution coefficients. At each of the m time scales the signal is convoluted by the DWT with distinct wavelet functions. The daughter wavelet functions ym, n(t) (eqn.1) are equal to the expanded and translated mother wavelet functions у [19].

ym, n(t) = 2-m/2 y( 2-m t — n) ; m, n є Z; t є ^ (1)

Where m defines the scaling or expansion of the mother wavelet and n defines the translation of у, relatively to the time t of the time series values from the signal to be analyzed. Due to the expansion, the convolution support lengths are increased by the factor two from scale m to m+1. For the DWT, the wavelet convolutions are obtained by a filter bank of Finite Impulse Response (FIR) digital filters [19] (Figure 1a). The filter bank separate by low and high pass filters the signal to be analyzed in signals with distinct frequency bands. The mother wavelet (Figure 1a — first bk filter) represents the FIR high pass which separates the highest frequencies appearing within the bandwidth of (SL -1 … ГО). SL is the support length of the mother wavelet. The low pass filters ck, also named as scaling function, represent on its output the signal with the complementary low frequency band until to zero frequency. At m = 1, e. g. the complementary frequency bandwidth is (0 … SL-1) and for m = 2 its frequency content decrease to (0 .. .(2SL)’1). The frequency band of the high pass filter at this scale is ((2 SL)-1… SL-1) and from scale m to (m+1) its band width is reduced by the factor two. Where in the Fourier transform the frequency bins are hold constant, in DWT the energy is hold constant to obtain nearly complete reconstruction of the original time series signal. The signal details and approximations at distinct time scales or filter bands are obtained by the bk and ck filters (Figure 1a). The last scaling function is also known as father scaling function [20].

The downsampling function (2f) after each filter reduces the vector length by two, avoiding a redundant representation of the decomposed signal and due to the upsampling (2t) the signal is reconstructed to its original vector length. The decomposed signal can be represented by the wavelet and scaling coefficient vectors T(m, n) and S(m, n) (Figure 1), or by equal length partially reconstructed sub-signals. If during the reconstruction of the original signal, utilizing the inverse filter bank (Figure 1 b), only one of these vectors is supplied to its input, the signal which corresponds to the supplied vector, is reconstructed to the length of the original time series. This wavelet transform is also referred as Non Decimated Wavelet Transform (NDWT), or a trous WT and its partially reconstructed signal vectors are here named as sub-signals. Beside the

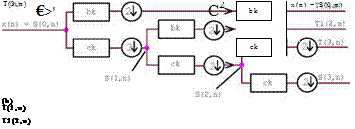reconstruction based on the wavelet and scaling coefficients (Figure 1 b), with the NDWT one can reconstruct the original signal by the sum of the complete sub-signal set.

Cf(1,k)

Cf(2,k)

Figure 1 — Wavelet digital filter bank for the decomposition of a signal (a) and its reconstruction (b), where ( 2i ) stands for the downsampling process and ( 2t ) stands for the upsampling process