The applied approach splits the total load curves into shiftable and fix parts, where the shiftable power is assumed entirely redistributable over the day. When considering net production and demand profiles, net production can be represented as negative demand. The DSM strategy then refers to the more general case of valley-filling measures, leveling out demand sinks. Computationally, this means finding an optimal power level such that filled-in energy below this level equals the shiftable energy. This approach gives an upper level to the achievable load matching improvement through DSM.

Two cases (2a and 2b) are defined, where in the first case the shiftable demand is that from washing, drying and dishwashing appliances that could be easily rescheduled and involve relatively little user interaction. The second case involves all end uses except lighting, cold
appliances and undefined additional demand, and implies considerable violation of everyday routines.

2.2. Storage

A third option for increased load matching is introducing small storage units as buffers between the PV system and the distribution grid. To study the effect of such systems a simple battery model is applied. When the PV system overproduces power, the battery stores energy up to the battery capacity EUm. At net demand, the battery unloads energy with an efficiency kejf. State-of-charge limits for avoiding deep-charging are not included in the model. In the case studied here (case 3) a storage size EUm of 1 Wh/Wp is used and an efficiency kejf of 0.8.

3. Results

In Fig. 4, it is possible to comprehend the performance of a PVT hybrid system when it comes to thermal and electrical outputs interaction. As it is represented, when an electric load is connected to the electric circuit, electric power can be extracted. This means that part of the incoming irradiation is transformed into electricity by the PV cells instead of being absorbed by the thermal receiver. Hence, the thermal output decreases as much as the electrical output is extracted.

3.2. Reflector optical accuracy and design

Given that the measured system electrical efficiency (8.3% at 25°C) is significantly lower when compared with the bare cells efficiency (16% at 25°C), experiments were carried out in several components accuracy in order to estimate their influence in the final electric and thermal output breakdown. One of the most significant inaccuracies relates to the reflector. Ideally, every light beam perpendicularly incident to the glazed cover of the trough should be reflected to the PV module. Laser beam tests were carried out during the night and the glazed areas where the light was not focused on the PV cells were marked and are illustrated in Fig. 5. I-V curves were measured with and without the covers and the electrical output was roughly the same. The glazed marked area is approximately 15% of the total glazed area and can represent an optical efficiency margin of improvement on the reflector accuracy for future Simulation and calculation

E. Yandri[2]* N. Miura1, T. Kawashima1, T. Fujisawa1, M. Yoshinaga2

1Solar Energy Research Group, Department of Vehicle System Engineering, Faculty of Creative Engineering,
Kanagawa Institute of Technology, 243-0292 Atsugi, Japan

2Department of Architecture, Faculty of Science and Technology, Meijo University, 468-8502 Nagoya, Japan

Corresponding Author, yandri@ctr. kanagawa-it. ac. jp

Abstract

A Hybrid Photovoltaic Thermal (PV/T) collector is an integration of photovoltaic and solar thermal technologies into one system. The idea behind the hybrid concept is that a photovoltaic (PV) cell converts only 6-15% of the incoming solar radiation into electricity and more than 85% of the solar energy is either reflected or converted into heat. PV/T is designed to produce both electricity and thermal energy simultaneously in order to give the highest solar energy conversion efficiency comparing with the separated system into photovoltaic panel and solar thermal collector with the same area. Many researchers have done a lot of efforts to improve its performance by experimentally and simulation analysis. This paper presents the analysis of experimental result for PV/T, focusing on the thermal efficiency with and without electricity generation. The experiment was done during the peak irradiation from 12.00 to 14.00, in the steady state condition. The flow rate is 4 l/min, the inlet water temperatures to the collector is 120C. Especially for this experiment, the result shows that the thermal efficiency of a PV/T is not changed significantly comparing with and without electricity generation. The heat loss for without electricity generation case is a bit higher than without electricity generation case which might influenced by the higher wind speed for without electricity generation case than with electricity generation case.

Keywords: PV/T, thermal efficiency, electricity generation, overall heat transfer coefficient

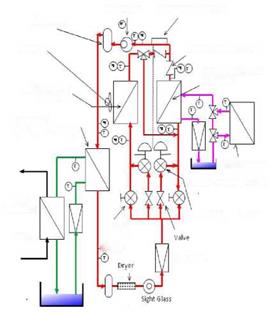
panels and solar thermal collectors. This is the ideal solution if the availability of the roof area is limited. The most common PV/T collector type for low to medium temperature applications follows the sheet and tube heat exchange design shown Fig.1, typically consist of PV module on the back of which and absorber plate (a heat extraction device) is attached. The purpose of the absorber is to cool the PV module which resulted improving the efficiency and to collect the thermal energy produced. The PV plate is fixed on to the absorber plate through a thin adhesive layer. The adhesive layer used is a material with good thermal conductivity, is resistant to extreme temperatures and is extremely improved electrical insulator.

Many researchers and institution have attempted to develop and evaluate the hybrid PV/T collector performance experimentally and analytically. Ito and Miura, experimentally and analytically studied the thermal performance of a PV/T collector that used a partially transparent PV module as a cover [2], [3]. Ito and Miura also reported that the collector efficiency was slightly less while generating power than while not generating power [4]. Othman et al. [5], studied theoretically and experimentally hybrid PV/T solar collector regarding its thermal and electrical performance, used air as a flowing fluid to extract heat from the photovoltaic cells and keep electrical efficiency of it a satisfactory level by the reduction of its operating temperature. The conclusion of this work this work is that is important to use fins as an integral part of the absorber surface in order to achieve meaningful efficiencies for both thermal and electrical output of the hybrid PV/T solar collector. Santbergen and Zolingen simulated various crystalline silicon solar cell configurations found that a standard untextured solar cell with a silver back contact has an absorption factor of only 74%. If a semi transparent solar cell is used in combination with second absorber the total absorption factor can increase to 87%, and if irradiance is absorbed in the back contact, the absorption factor can increase to 85%. They suggested to apply the rough interface in combination with a non standard metal as back contact [6].

The total efficiency of a PV/T npv/t is by adding the thernal efficiency and electrical efficiency Пе1 which can formulated as below

npvt =Ъг +Пе1

The thermal effciency of a PV/T collector is defined as the rasio of the useful heat Qth [W] to the product of the aperture area Ac [m2] and the insolation I [W/m2], which is incident on the aperture [1]

Qth

AI

The useful heat Qth [W] is related to mass flow rate m [kg/s], spesific heat at constant pressure cp [kJ/kgoK], and inlet an outlet temperatures Tn [oK] and Tout [oK] [1]

Qth = mcp (tn — tout) (3)

The efficiency may depend on many factors; collector temperature, ambient temperature, insolation, flow rate, and the incident angle. In order to characterize a collector, one must therefore specify the conditions under which the efficiency has been measured or calculated. One would like to specify the conditions in such a way that the efficiency is defined unambiguously and can be measured reproducibly. This can be accomplished most easily if one bases the effciency on clear sky conditions.

The electrical effciency це1 of a PV/T collector is defined as the rasio of the power generated Qel [W]

to the product of the aperture area A [m2] and the insolation I [W/m2], which is incident on the aperture [1]

The the power generated Qel [W] is related to current Iel [ampere] and Voltage Vel [volt] generated by the solar cell [1]

Qei = IV

The common linear formula of the thermal efficiency is [7]:

Пп = Fn O-U ((,, — Ta )/I ] (6)

Where T is transmittance, a is absorptance, the product of та is the optical efficiency no, U is the collector heat loss coefficient, and I is irradiation. Fin is called the heat removal factor, defined by the equation [7]

Where Fm is called the collector efficiency factor that accounts to the resistant of absorber to the ambient Rabs amb and the resistant of front to ambient Rfr amb [7]

b. Schematic experiment set up

Fig.1. PV/T and experiment set up

2.

Result and Discussion

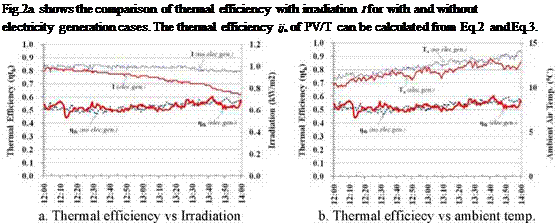Fig.2. Thermal efficiency vs irradiation and ambient air temperature.

For with electricity generation case, the irradiation I is decreased approximately from 1000 W/m2 at 12.00 to 770 W/m2 at 14.00. For without electricity generation case, the irradiation I relatively steady approximately 1000 W/m2. The average thermal efficiency i)th for with electricity generation case and

without electricity generation case was relatively about the same. They are 0.5258 for with electricity generation case and 0.5268 for without electricity generation case. Fig.2b shows the comparison of thermal efficiency and ambient air temperature Ta. Although the irradiation I was decreased for with electricity generation case and steady for without electricity generation case, the ambient

temperatures Ta for both cases increased during those periods of time. During periods of 12.00 — 14.00, the average ambient temperature Ta was about 11.70C for with electricity generation case and 12.40C for without electricity generation.

Fig.3a shows the comparison of thermal efficiency nth with the average surface collector temperature Tcoll. The average surface collector temperature TcM for with electricity generation case was unsteady and smaller with average of 23.10C and 24.00C for without electricity generation case. Fig.3b shows the comparison graphs of the thermal efficiency rjth with the outlet water temperature Tout. The outlet

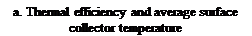
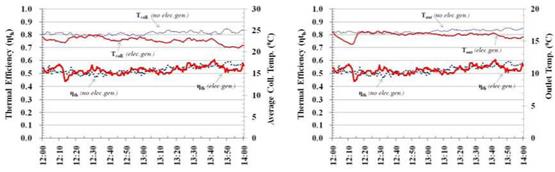water temperature for both with and without electricity generations cases were about the same in the period of 12.15 — 13.00, but from 13.00 — 14.00, they were relatively steady for without electricity generation case and decreased for with electricity generation case. It might be affected by the variation of the irradiation I. The average outlet water temperature Tout for with electricity generation case was about 15.9°C and 16.5°C for without electricity generation.

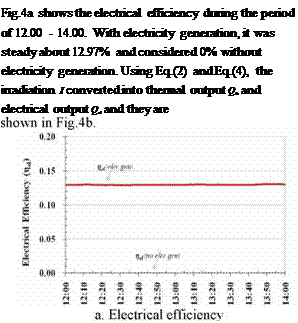
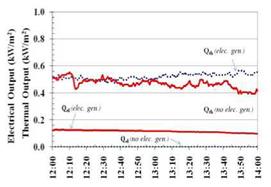b. Thermal and predicted electrical output Fig.4. Thermal efficiency vs irradiation and ambient air temperature As an effect of the trend of irradiation I, the thermal output Qth and electrical output Qet both with

electric generation also follow the same trend of irradiation I. It shows that the average thermal

output Qth for without electricity generation case relatively steady about 0.519 kW/m2 and decreased from 12.00 — 14.00 with average about 0.469 kWm2 for with electricity generation.

Fig.5a shows the scatter diagram of thermal output Qth vs (Tavg -Ta) /1 for with electricity generation

and without electricity. Fig.5b shows the scatter diagram of the thermal efficiency nth vs

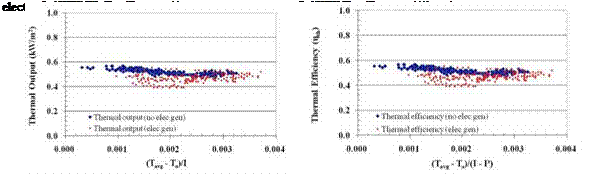
(Tavg — Ta) / (I — Qel) for with electricity generation and without electricity generation by excluding the

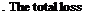
Fig.6a shows the comparison of total loss Qloss tot and the heat loss to ambient Qloss amb of this analysis is calculated by

Qloss, tot = 1 (1 — nth -Vel )

The total loss Q, is the sum of the top loss Q, , back loss Q, , , and edge loss Q, , ,

loss, tot loss, top loss, back loss, edge ‘

and Eq.(9) can be expressed also

Qloss, tot Qloss, top + Qloss, back + Qloss, edge (10)

To simplify the analysis, by assuming the ambient air temperature Ta and wind speed Vwind on the top and at the back of collector are about the same, and also neglected the edge loss Qt

focus to analyse the top loss Qloss t. Because of this experiment used on single cover PV/T, the top loss Qloss o involve are convection and radiation loss from absorber to cover and from cover to ambient and then the top loss Qloss tov can be formulated

q — Ah (T — T

loss, cov-amb, conv icov conv cov amb

Where. Aabs and Acov are the absorber and the cover area (m2), s is the emissivity (dimensionless, 0.88 for glass [7]), d is the Stefan-Boltzmann constant (5.67×10-8 W/m2K4), Tcbsis the absorber temperature (K), Tcov is the glass cover temperature (K), and Tamb is the ambient air temperature and hcotw is the convective heat transfer coefficient from the cover to the ambient air as a function of wind

velocity Kind

Bay assuming Tsky — Tair — Tamb and Eq.(11c) and Eq.(11d) can be simplified [7]

hamb (Tcov Tamb ) hconv (Tcov Tamb ) + Scovd(Tcov Tamb )

Knb is the effective heat transfer coefficient for both convection and radiation which has value of 20W/m2 for 3m/s wind speed and 30W/m2 for 6m/s wind speed [7]. To simply analysis,

assuming the radiative and convective from absorber to cover ( Qtoss, abs-cov,.rad and Qloss, abs-cov, conv ) more

or less the same for with electricity generation and without electricity generation, and the analysis

focus on the radiative and convective loss from absorber to cover ( Qioss, cov-amb, rad and Qloss, cov-amb, conv X

Loss energy ratio (LER) is the ratio of total loss Qloss tot divided with irradiation I and formulated in

LER — Qosso /1 (13)

Fig.6. Energy loss and wind speed

Fig.6b shows also the wind speed Vwind of with electricity generation was lower than the wind speed Vwind of without electricity generation. The average wind speed Vwind of with electricity generation was about 0.3 m/s and 1.1 for without electricity generation. Using Eq.(11.c), the radiative heat loss

from cover to the ambient Qloss cov-amb rad for without electricity generation relatively as same as with electricity generation. Using Eq.(11.d), the average convective heat loss from cover to the ambient Qioss cov-amb conv for without electricity generation was about 0.119 kW/m2, higher than the average

convective heat loss from cover to the ambient for with electricity generation was about 0.075 kW/m2. It proved that the wind speed has a significant effect to the ambient loss.

3. Conclusion

Especially for these experiments, some parameters, like irradiation, ambient temperature, were not so closed each other, they did not change significantly the thermal efficiency. It means that the thermal efficiency for with electricity generation is relatively as same as without electricity generation. The total loss Qloss especially for the heat loss to the ambient Q0ss cov-amb increased as same

as the wind speed increased. The analysis shows that the thermal efficiency formula in Eq.(6), (7) and (8) did not influence much to the parameters of collector heat loss coefficienct U, heat removal factor Fin, and collector efficiency factor Fm.

Acknowledgement

The support of “High-Tech Research Center Project for Private Universities: matching fund subsidy from MEXT, 2007-2011” for this research is appreciated.

References

[1] Duffie, J. A, Beckman, W. A., Solar Engineering of Thermal Processess (third edition), John Wiley & Sons, Inc. Hoboken, New Jersey

[2] Ito, S., Miura, N., Solar Air Collector Using Photovoltaic Modules as the Cover, Proceedings of ISES Solar World Congress, Budapest, Vol. 3, pp.271-276, 1993

[3] Ito, S., Miura., Usage of a DC Fan Together with Photovoltaic Modules in a Solar Air Heating System, Proceedings of ISES Solar World Congress, Gotheborg, Sweden, 2003.

[4] Ito, S., Miura, S., Performance of Photovoltaic and Thermal Hybrid Air Collectors, Proceedings of ISES Solar World Congress, Orlando, USA, Paper No. 1349, 2005

[5] Othman, M. Y., Yatim, B., Sopian, K., Bakar, M. N.A., Performance studies on a finned double­pass photovoltaic-thermal (PV/T) solar collector. Desalination 209 (2007) 43-49

[6] Santbergen, R., van Zoelingen, R. J.Ch., Modeling the thermal absorption factor of Photovoltaic / hermal Combi Panels. Heat Set 2005, Grenoble, France [3]

Two decks have been created one for heating mode and one for cooling mode, but the entire year can be simulated all at once. A 10 minutes time step has been selected to promote the convergence of some components, in particular the controllers.

Not many simulations have been carried out up to now. However, some considerable results have come out which already addresses on the way to an optimal planning. In fact, during the first simulations the following aspects have emerged:

• the absorption chiller matches well the cooling peak demand but it often switches on/off at low loads

(Fig. 6.);

• the solar fraction is quite small: boilers are required to run the whole year;

• the tank serving the cogenerator is small: the engine switches on/off whenever low flows are extracted from the top of the tank.

Please note: the on/off behaviour of the cogenerator and the absorption chiller is also due to the fact that thermal inertia effects are not included in both the mathematical models.

Fig. 6. Simulation of the cooling flow demand and the absorption chiller in a typical summer day.

2. Conclusions

SHC-CHP systems seem an interesting project solution but their planning requires a huge effort mainly due to the different behaviour of the solar collectors and cogeneration units. The procedure suggested in this paper is finalised to support the design of such plants in order that the mentioned components do not interfere in their respective operation. This procedure can be applied to whatever kind of building, its demand being known. Once the layout and the control strategy are fixed, the simulations address to the optimal solution in terms of size. The energy consumption corresponding to the final solution will then make clear whether and in which case this sort of project is energetically and economically convenient.

Acknowledgements

The authors would like to gratefully thank the STIFTUNG SUDTIROLER SPARKASSE for the financial support.

References

[1] Dorgan, C. B., Leight, S. P., Dorgan, C. E., 1995. Application Guide for Absorption Cooling/Refrigeration Using Recovered Heat. USA: ASHRAE.

[2] Petchers, N., edited by, 2003. Combined Heating, Cooling & Power Handbook: Technologies & Applications. Lilburn, GA: Fairmont Press.

[3] Troi, A., Filippi, H., Sparber, W., 2005. Practical Experience with Solar-Assisted Cooling in an Office and Educational Building in South Tyrol / Northern Italy. In: Otti, ed., 2005. 1st International Conference on Solar Air Conditioning. Germany, October 2005.

[4] Nurzia, G., 2008. “Design and simulation of solar absorption cooling systems”. PhD Thesis in Energy and Environmental Technologies, Department of Industrial Engineering, Bergamo University.

The prototype built followed the design presented in figure 2. This system incorporates a PV-cell 150mmx150mm, Pmax=1,12W, (Polycrystalline Silicon wafer) and the whole structure is made of aluminium alloy. In fig. 6 the global developed prototype is shown. The control unit was developed using an industrial Siemens S7-300 PLC (Programmable Logic Controller). Figure 7 details the electro-mechanical structure of the developed sun-tracker system.

The selected PLC system is a modular device that is constituted by the following modules:

Slotl = Power supply PS 307-2A Slot7 = Analog card AO4 x12bit

Slot2 = Processor CPU 315-2DP Slot8 = FM card — Counter Module (FM350)

Slot4 = Communication module CP 342 -5 Slot9 = FM card — Counter Module (FM350)

Slot5 = Digital card DI8/DO8xDC24V/0,5A SlotlO = FM card — Stepper Motor (FM353)

Slot6 = Analog card AI8 x12bit Slotll = FM card — Stepper Motor (FM353)

Additionally, the PLC-tracker has a modem for GSM communication that provides the system capacity to communicate through the mobile phone network.

Using TRNSYS the PVT system was modelled with a flow rate of 300 kg/hr (0.083 kg/s), equivalent to one building air change per hour, and with zero air flow, as would be the situation for a non-ventilated building integrated PV system. The results showed a difference of at most 1.3% between the PV efficiency operated under these two conditions, however, over the course of the year this small difference in PV efficiency results in quite a substantial increase in electrical output for the ventilated PVT system. This value was calculated to be 135 kWh/annum, assuming a PV cell packing factor of 0.85 and a value of 0.92 for transmission through the glass cover.

Because electricity can be fed into the distribution grid, grid restrictions are with a moderate penetration of RES actually not the limiting factor. But with a higher amount of decentralised production the transport capacity of the grids will be reached. Variable tariffs give a soft stimulation for operators to shift their operation schedule.

In [6] the Association for Electrical, Electronic &Information Technologies (VDE) suggests a feed-in tariff based on the day-ahead price at the European Energy Exchange in Leipzig (EEX). To the variable EEX-price a constant bonus for decentralised plants will be added during the high demand time from 6 am to 1 am. In the following this scenario will be called VDE.

The described grid in section 1 defines a very weak grid, where the global VDE-tariff might not control decentralised plant sufficient. For an efficient grid operation it is desirable to produce most of the needed power within the grid. For that reason we modified the constant bonus in the VDE-tariff to a local component. This scenario will be called LOCAL. For that the net load (difference between electric load Pel and photovoltaic production PPV) was used. This load was spread to a local time dependent bonus with a minimum at 0°cent and the mean value at the bonus in the VDE-scenario. If the missing power is large the tariff will be high to stimulate further decentralised generation.

To compare the results we assumed the typical constant feed-in tariff for cogeneration in Germany, which is called KWK-G.

3.1. Electrical performance

During this study it was not possible to measure the cells temperature directly since the trough structure is closed. Hence, the average water temperature running inside the thermal absorber at the moment of the electrical efficiency measurement is presented instead. Using the maximum electric power extracted by Solar8 together with the incident beam irradiation it was possible to estimate the electrical efficiency behaviour of the system depending on its working temperature (Fig. 2).

From the linear representations of the electrical performance it is possible to estimate that the electrical efficiency is 8.3% per active glazed area and 6.3% per total glazed area at 25°C average water temperature running inside the thermal absorber. The slope of the electrical performance trend lines fits fairly close the classical 0.4% drop in efficiency per °C in cells temperature increase. For this study, active area was defined as the maximum glazed area the system can make use of.

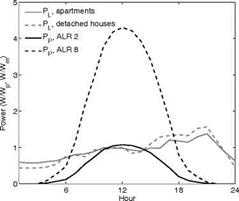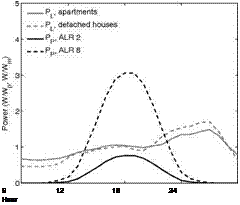
The following results are presented for two setups with different relative demand-to-production ratios, corresponding to different PV penetration levels. The array-to-load ratio (ALR) is the ratio of nominal array peak power to the mean load, in this case the annual mean load for detached houses. Two system setups with ALR of 2 and 8 are used. The relative sizes of load and production are shown in Figure 2. The first setup results in a small overproduction, corresponding to a penetration slightly above optimal from the grid point of view (cfr. [3]). The second setup causes a massive overproduction but nonetheless yields just enough to annually cover the household electricity demand.

Fig. 2. Average load (PL) and production (PS) for the whole year (left) and the summer months May, June
and July (right) at different relative system sizes (ALRs). In addition to the load profile for detached houses,
the corresponding load profile for apartments is shown for comparison purposes.

The main indicator of load matching considered here is the solar fraction, which is the fraction of load covered by PV. Since the overproduced power level is critical from the grid point of view, this is covered briefly.

The model of the power outputs calculated in the performed simulations is described by the following equations and parameters [2].

P = ‘HobKtaGb +^odGd — a1((Tout+Tin)/2-Tamb)- a2((Tout+Tin)/2-Tamb)2 (1)

where Kta = 1-bo(1/cos0-1) (2)

qod=Kdiffuse*qob (3)

Simulation Parameters: