1.1. Background

The International Energy Agency (IEA) initiated Task 35 "PV/Thermal Solar Systems", a three year research program, on January 1, 2005, as part of the IEA Solar Heating and Cooling (SHC) Program. The objectives of this Task were to catalyze the development and market introduction of high quality and commercial competitive PV/Thermal Solar Systems, to increase general understanding of PV/T and contribute to internationally accepted standards on performance, testing, monitoring and commercial characteristics of PV/Thermal Solar Systems in the building sector.

The definition of PV/Thermal solar system is a combination of photovoltaic (PV) and solar thermal components which produce both electricity and heat from one integrated system from the same surface area exposed to the sun. PV and solar thermal panels which operate side by side and not together are excluded from this definition

The following main components have been included in the plant scheme (Fig. 4.):

• vacuum tube (VT) collectors;

• one co-generation unit based on a reciprocating gas engine and controlled by the heat load;

• one absorption chiller.

The VT collectors and the cogeneration unit are connected in parallel. Biomass boilers have been selected to assist the heat production with a renewable source. One compression chiller gets involved whenever the absorption chiller does not match the entire cooling demand. Solar collectors are exclusively connected to a storage tank. Thus, the solar fraction is only used when the tank reaches selected temperature levels and heat is required at the same time, otherwise it is stored. Also the cogeneration unit is served by a tank. However, in this case, the storage is employed to buffer the variable load and to prevent that the engine frequently switches on/off. The selected DS consists of radiant panels and fan coils, respectively for heating and cooling mode. It is connected to the heating and cooling facility by means of a heat exchanger. Therefore, the medium flowing through the DS is different from the one flowing through the facility. In this way, the variation of the heating and cooling demand, i. e. the variation of the mass flow in the DS, is smoothed and the machines can operate under more stable conditions.

Joao M. G. Figueiredo1*, Jose M. G. Sa da Costa2

1 CEM-IDMEC, Universidade Evora, R. Romao Ramalho, 59; 7000-671 Evora, Portugal
2 IDMEC-IST — Technical University Lisbon, Av. Rovisco Pais; 1049-001 Lisboa, Portugal
* Corresponding Author, jfig@uevora. pt
Abstract

The growing concerns of global warming and depleting oil/gas reserves have made it
inevitable to seek energy from renewable energy resources. The positive impacts of an
increasing share of renewable energy on the mitigation of climate changes are indisputable.

This paper proposes the optimization of the electric energy production by photovoltaic cells through the development of an intelligent sun-tracking system. The developed solution has many advantages in relation to similar existing devices, as this system is autonomous regarding the information needed to process the optimal orientation and is intelligent in a way that it performs on-line monitoring of the photovoltaic energy production.

An experimental prototype was built and field results have proven the good performance of the developed tracking system.

The observed increase in power generation, in relation to other PV-systems, without tracking devices, is of similar magnitude (ca. 25%) as for other usual tracking solutions. However, this system has a relative advantage, as it measures exactly the controlled variable: the actual PV-power generation.

Keywords: Photovoltaic Cells, Tracking Systems, Intelligent Sensors, Supervisory Control.

1. Introduction

The use of new efficient photovoltaic solar cells has emerged as an important solution in energy conservation and demand-side management during the last decades. Owing to their initial high costs photovoltaic solar cells have not yet been an attractive alternative for electricity users who are able to buy cheaper electrical energy from the utility grid. However they have been used, as the wind turbines have been used, for water pumping and air conditioning in remote and isolated areas, where utility power is not available or is too expensive to transport.

Although solar cell prices have decreased considerably during the last years due to new developments in the film technology and manufacturing process [1], photovoltaic arrays are still considered rather expensive compared with the utility fossil fuel generated electricity prices. After building such an expensive renewable energy system, the user naturally wants to operate the photovoltaic infrastructure at its highest conversion efficiency by continuously utilizing the maximum available output power.

Nowadays photovoltaic energy has a low efficiency ratio concerning the complete distribution chain from production to consumption (ca. 12%). In optimized environments (materials, electric inverters, tracking systems, etc) an input of 1000W of solar incident energy can bring ca. 190W in electricity (efficiency of 19%). This low performance ratio implies big Earth surface consumption when it is intended to install industrial photovoltaic units with significant production impact (50MW — 100MW). Today it is being built in Portugal a photovoltaic plant with 64MW production capacity which occupies an huge area of ca. 400 ha (4 Km2).

The more relevant side effect of the low efficiency of photovoltaic systems is its poor competition related to traditional combustibles in both economical and financial aspects.

It is urgent to improve the production efficiency of electricity from the Sun as this energetic source is the most powerful in our planet, and it is expected that the Sun will become the main electricity production source by the year 2100, according to the study presented by the German Advisory Council on Global Change [2].

Owing to changes in the solar radiation energy and the cell operating temperature, the output power of a solar array is not constant at all times. Consequently, a maximum solar power tracking controller is always needed in any scheme with solar cell arrays to ensure maximum utilization. Therefore, works to solve the problems on maximum power point (MPP) tracking have always been a hot topic for photovoltaic array utilization systems. A logical MPP tracking search algorithm using normalized current, voltage and power at the work points that corresponds to the maximum power point values for different operating conditions was introduced earlier by the same authors [3, 4]. A on-line controller to track the MPPs under changing illumination was described in

[5].

An optimization approach using fuzzy was given in [6] for PV water pumping systems. Other MPP tracking controllers can be found in [7, 8].

In this paper an intelligent sun-tracking system for efficiency maximization referring photovoltaic energy production is developed. The developed tracking system is innovative in relation to the usual sun tracking systems available in the market.

The usual available solutions for tracking systems rely on the knowledge of the geographical position of the solar panel on the earth surface. With this knowledge it is possible to know the relative position of the sun, on a time basis, according to the well known solar tables [9]. Modern solutions incorporate a GPS system to calculate the position of the solar panel on the Earth surface. The orientations to be followed by the photovoltaic panel, on a regular time-base, are then pre­programmed, on an open loop approach.

There are significant efforts on the optimization of sun tracking systems as it is documented by several registered international patents. These solutions are based either on the above described principle either on the quantification of the received solar energy, either on the maximization of the solar incident radiation through the use of light concentration lens [10], [11].

The solution developed in this paper is innovative related to the above referred approaches as this system is autonomous regarding the information needed to process the optimal orientation and it is intelligent in a way that it monitors, on a real-time base, the photovoltaic energy production and it avoids systematic failures coming from changes on the assumed values (position, initial infrastructure orientation, cleanness of the photovoltaic cells, etc.).

2. Developed System

Building energy modelling was conducted using TRNSYS and the equation based IDA Indoor Climate and Energy (ICE) building energy simulation programs. TRNSYS was used as a PVT component Type 567 was available as part of the Green Building Component Library and this component interfaces with the Type 56 Multi-zone building. The key parameters and inputs used for simulating the PVT system in TRNSYS are outlined in Table 1. The PV efficiency modifier parameter is used to account for a reduction in the power output of the PV due to an operating

temperature above the standard 25 °C test conditions. IDA ICE was also used to create a model of the house and determine the heating energy requirement. TMY2 weather data for Sydney was used for simulations in both programs.

The HDD method was used to conduct a simple analysis of the building heating energy requirement. Equations detailed by Eicker [7] for evaluation of the temperatures and performance of building integrated photovoltaic facades and solar collectors were followed to validate the simulated thermal energy output results from TRNSYS.

Table 1. Key parameters and inputs used for simulation of the PVT system in TRNSYS

The main parameters of the plant configurations discussed in this paper are listed in Table 1. Pretorius [2] found that plants with larger chimney diameters provide lower COE. The effect of varying the chimney diameter is investigated using two base configurations with a 1000 m and a 1500 m high chimney.

The question of how big a first large-scale solar chimney power plant should be has been asked many times. To reduce the risk for a first prototype, building a smaller plant could be an option.

The implications on the design of the PCU of building such a smaller plant are discussed in this paper. The most promising options to improve the plant performance, which are double glazing the collector and applying anti-reflective coating [2], are also investigated.

3. Results

The multiple horizontal axis turbine configuration using a single rotor layout with IGVs provides the lowest cost of electricity for all plant geometries investigated here. The optimum number of turbines is 10 for the smallest plant and 42 for the biggest plant. The optimal turbine diameter is 31 m for the smallest plant and 41 m for the biggest plant. The lowest COE was found with Configuration 8 (Tab. 1) at 0.105 €/kWh. The COE for the smallest plant is 2.5 times higher due to a much lower annual power output.

Reducing the number of turbines below the optimum increases the COE mainly because of a decrease in efficiency and an increased generator cost. Increasing the number of turbines beyond

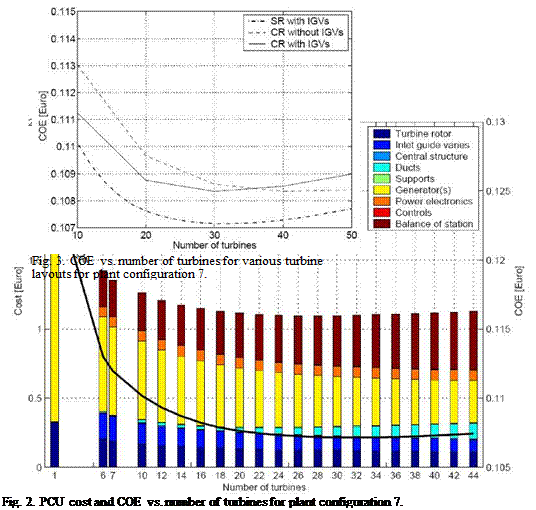the optimum increases the COE mainly because the reduction in generator cost is outweighed by the cost for transportation, for the ducts and for assembly and installation (see Figure 2). The counter rotating turbine layouts show similar trends as the single-rotor layout with IGVs. They provide a COE which is only about 1 % higher than the one of the single-rotor layout with IGVs (Figure 3).

Solar chimney cost models found in the literature either assume a constant specific initial cost (€/kW) for the PCU, or they assume the cost of the PCU to be a constant percentage of the sum of

the collector and chimney cost. The specific initial cost of the PCU resulting from the model presented here ranges from 437 to 1644 €/kW for the various plant geometries. The PCU cost as a percentage of the sum of the collector and chimney cost ranges from 17 to 30 %.

On the example of Configuration 5 it is shown that the implementation of double glazing and anti­reflective coating holds a potential to significantly reduce the COE of the solar chimney power plant. With the models chosen in this study the cost of electricity is reduced by 17.8 %. The annual power output increases by 51.7 % while the initial investment cost only increases by 26.0 %.

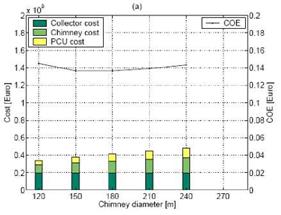
As can be seen from Figure 4 and Tables 2 and 3, the notion to use larger chimney diameters, as brought forward by Pretorius [2], can indeed be supported; for the plant with a 1000m high chimney the optimum chimney diameter is between 150 and 180m. For the plant with a 1500m high chimney, the optimum chimney diameter is 190m. These values are higher than the ones cited in earlier publications. But they are also significantly lower than the ones suggested by Pretorius

[2]

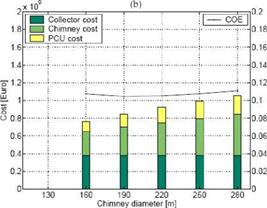(210 m for the 1000 m high chimney and 280 m for the 1500 m high chimney). This is because the plant cost model and the cost model for the PCU used here are more sensitive to a change in chimney diameter than the ones of Pretorius (2006) as the collector cost is less dominant.

Fig. 4. Plant cost and COE vs. chimney diameter for the reference plant with (a) a 1000m and (b) a 1500m

high chimney.

Tab. 3. Results for various chimney diameters for the plant with a 1500m high chimney.

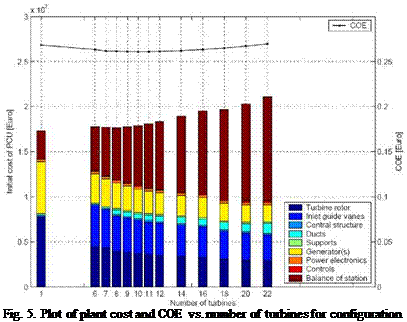For a smaller plant (configuration 1) a PCU with 10 horizontal axis turbines provides the lowest cost of electricity (Fig. 5). Even though the overall plant cost for this small plant is only a fraction of the cost of a large plant (e. g. a tenth of the cost of configuration 7) the optimal cost of electricity is 2.5 times higher due to a much lower annual power output. In comparison to configuration 7, for the smaller plant discussed here, the generators, the electrical interface/connection, the power electronics and the ducts contribute a much smaller portion to the PCU cost. In contrast, the inlet guide vanes, the turbine rotors, transportation as well as assembly and installation contribute a much bigger portion. The cost of the chimney for this plant is 21.82M€, the cost of the collector 30.77M€. The initial capital cost of the PCU is between 17.30 and 20.31M€, which is equal to 32.9 to 38.6% of the sum of the cost of the collector and the chimney. This is a much bigger portion than for the larger plants. As a consequence the optimal diffuser area ratio is higher for the smaller plant and the efficiency of the PCU is reduced.

4. Conclusion

For all plants discussed here PCUs with multiple horizontal axis turbine configuration using a single rotor layout with IGVs provides the lowest cost of electricity. For the counter rotating turbine layouts the cost of electricity is only 1.1% higher than with a single rotor layout with IGVs.

While the size and performance of the different plants vary a lot, the optimal PCUs all look very similar. The optimal number of turbines varies, but their individual size, the number of blades and even the efficiency of the PCU remain close to constant. The cost of the PCU, however, varies significantly; the specific initial cost of the PCU varies between 437 and 1644€/kW.

A large plant with e. g. a 1500 m tall chimney provides a low cost of electricity and a high annual power output. But the financial (and technological) risk is also high. Moving towards smaller plants the risk is reduced. But the annual power output is also reduced, and the cost of electricity increases. Measures like double glazing and anti-reflective coating could counteract this trend.

Acknowledgements

The authors would like to express their gratitude to the VolkswagenStiftung, Germany, and to the National Research Foundation of South Africa for financial support. They would also like to thank Dr. J. P. Pretorius for providing the plant simulation results.

References

[1] Schlaich, J., Schiel, W., Friedrich, K., Schwarz, G.,Wehowsky, P., Meinecke, W. and Kiera, M. (1995). The solar chimney — Transferability of results from the Manzanares solar chimney plant to larger scale — plants. Tech. Rep., Schlaich Bergermann und Partner, Civil Engineers, Stuttgart, Germany.

[2] Pretorius, J. P. (2006). Optimization and Control of a Large-scale Solar Chimney Power Plant. Ph. D. thesis, University of Stellenbosch.

[3] Pretorius, J. P. and Kroger, D. G., Critical evaluation of solar chimney power plant performance. Solar Energy, 80 (2006) 535-544.

[4] Bernardes, M. A.D. S. (2004). Technische, okonomische und okologische Analyse von Aufwindkraft — werken (Technical, Economical and Ecological Analysis of Solar Chimney Power Plants). Ph. D. thesis, Universitat Stuttgart. (in German).

[5] Denantes, F. and Bilgen, E., Counter-rotating turbines for solar chimney power plants. Renewable Energy, 31 (2006) 1873-1891.

[6] Fluri, T. P. (2008) Turbine Layout for and Optimization of Solar Chimney Power Conversion Units. Ph. D. thesis, University of Stellenbosch.

[7] Fluri, T. P. and Von Backstrom, T. W. Performance analysis of the power conversion unit of a solar chimney power plant, Solar Energy Journal, (2008) accepted for publication.

[8] Riggs, J. L., Bedworth, D. D. and Randhawa, S. U. (1996). Engineering Economics. 4th edn. McGraw-Hill.

[9] Schlaich, J. (1995). The Solar Chimney — Electricity from the Sun. Edition AxelMenges.

1.1. Advantages of PV/T technology

PV/T technology combines photovoltaic (PV) generation of electric current and thermal (T) conversion of solar energy. In accordance with the laws of engineering system [1] evolution of a technical system life can be represented as S-shape curve (Fig.1). The curve S shows the most important technical parameters Ps (output power, efficiency, cost, life time etc.) depending on time.

The different technical systems certainly have individual peculiarities, but generally we can see three main areas. In “childhood” the systems are developed quite slowly. Then in maturity technical system’s parameters are improved very fast, the mass production begins and financial investments usually facilitate improving the systems. The third low growing and saturating area corresponds to aging of systems, where physics and technical limiting factors are practically

achieved. A new technical system should appear to achieve better parameters (Sn curve on Fig. 1). In our case, for example, photovoltaic (PV) system after achieving the limiting parameters can be improved only on jumping to a new approach, for instance, using multiplayer solar cells (SC) instead of one p-n junction in SC, or developing combined PV/T systems. Now it is possible to have efficiency already close to 40 % for multiplayer SC if to use only PV conversion. Total efficient of PV/T systems can be even much higher. Sometimes after saturation on the third stage of elaborating a certain degradation of output parameters can be observed (dashed line, Fig.1).

One example from solar engineering can illustrate this evolution behaviour of technical production. You can buy multi colored solar cells, but they cost more and deliver a little less energy. However, architects prefer them for aesthetic reasons. Even such decreasing of output parameters is patented. The invention [2] provides a colored solar cell unit where the application of the color need not be at the expense of the solar cell unit’s output.

The main advantage of PV/T hybrid systems is their high total efficiency. A logic of developing new solar systems demands both types of solar conversion.

That is why more and more publications are devoted to combined PV/thermal systems last years (see, for example, following references from [3, 4]).

Co-generation of heat and electricity is a good factor for integrating solar energy systems into buildings. Our analysis shows a general tendency of integrating of different solar energy technology. Chart at Fig.2 reflects this tendency of integrating classical solar energy technologies with modern ones [3].

The model for generation of load profiles has been described and validated in [5] and [6]. It constructs household electricity load profiles for a number of end uses by adding appliance loads together, according to use patterns described by time-use data in a representative sample of Swedish households. In this respect it can be classified as a bottom-up model, similar to that in [7].

The model is dependent on (a) time-use data, (b) data on mean appliance powers and (in some cases) maximum appliance runtimes and (c), for modeling of lighting, data on daylight availability. The time-use data set used, collected by Statistics Sweden, has undergone thorough examination and has been used previously in activity visualization studies (see for example [8]). Representative appliance characteristics were collected from publicly available product tests from the Swedish Consumer Agency [9] and daylight availability data were generated for a standard building in Stockholm with Satel-Light [10].

The resulting load data consists of annual series of aggregated hourly electricity demand for 11 different end-uses in the almost 200 households in the time-use data set, corrected for seasonal variations and validated for consistency against preliminary results from ongoing large-scale measurements performed by the Swedish Energy Agency [11].

The magnitude of the natural convection heat transfer is related to the mass flow rate of the air, which is established by the dynamic balance of two opposing effects: buoyancy and friction. Inherent to the flow inside the duct, are the pressure difference between the inlet and outlet air of the channel since the mean air temperature along the axial length of the duct in the flow direction will change (constant heat flux).

2.3 Driving Forces

It would be expected that the presence of these structural element will increase both the heat transfer rate and the hydraulic pressure loss. Under natural convection, the pressure drop due to the buoyancy forces is a result of the temperature difference between the heated surface and the column of the air in the duct. At a typical height (x) from the base corresponding to length (Lx) of the duct, the buoyancy pressure drop is given by [3].

APbx = PmgPexp(Ta, x — Ta, i )Lx sin P

4.2. Resistance to Flow

In the absence of hydraulic losses (variable cross sections, losses through valves, orifices, elbows), the resistance to flow in the channel is resumed to the friction pressure drop (Ap) and was computed as

[10] :

APf = pghf (14)

where, the friction head loss ( h ) is given by:

L V2

duct m

2 gDh

Therefore the pressure drop is expressed as:

P йиеУm

2 gDh

For a given BIPVT system, the choice of the duct length (Lduc{) is determined by the dimension of the

roof and therefore any design to optimise energy and heat transfer will be determined by the duct dept. The friction factor (f) for laminar and turbulent flow were respectively evaluated as suggested by Tsuji

[11] , and Smolec [12].

f = 1.906(Gr Pr)1/12

f = 1.368(Gr Pr)1/119

3. Experimental Results

5.1. Data Analysis

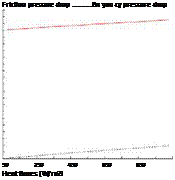
The steady state values were recorded over a period of time. Due to measurement fluctuations in the experiment a statistical uncertainty analysis was conducted. Initial analysis of the raw data yielded the mean and standard deviation of the measurements. Assuming the measurement fit a normal Gaussian distribution, the uncertainty was then calculated with a confidence level of 95%. The error propagation method was used and the average data evaluated. Figure 6 gives the magnitude of friction losses.

Figure 7. Magnitude of pressure drop under Figure 7. Temperature distribution on top plate along

natural convection the duct length at H = 4 cm, slope angle = 44°

It can be seen from figure7, that at a specific heat flux, buoyancy forces can be neglected.

In figure 7, the temperature decrease at the entrance and at the exit is due to radiation losses. Applying a polynomial form of the 6th order to the test data, the temperature distribution as shown in figure 10 can be expressed as:

T(x) = 36.92×6 — 245.8×5 + 605.0×4 — 673.4×3 + 316.8×2 + 0.248x + 55.37

R2 = 0.99

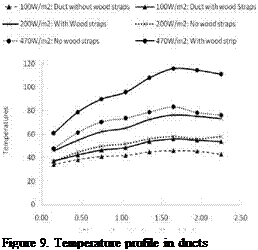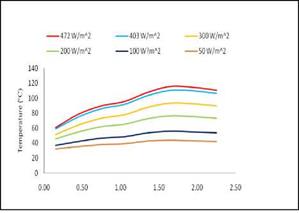
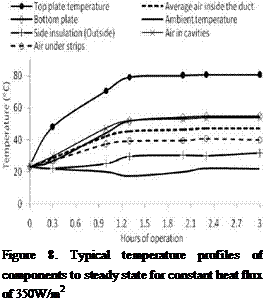
Figure 8 shows a typical temperature profile of components at steady state at a constant heat flux of 350W/m2, while illustrates the variation of the local air velocity as function of various heat fluxes.

As illustrated in figure 8, the air temperature under the wood strips Ta2, Ta4, and Ta6 (figure 2) remained lower than the air temperature in the cavities (Ta1, Ta3, Ta5, Ta7). At steady state the air in the cavities and the bottom plate have the same temperature.

As expected, the presence of the structural elements in the channel constituted an obstacle to the air flow inside the channel due to the increase in pressure drop and friction losses. Consequently, under the same constant heat flux, the reduced air flow rate in the channel due to the wood strips led to an increase in the components temperature as compared to the system without wood strips as illustrated in figure 9.

4. Conclusion

Experimental investigation of temperature distribution in a BIPV system under natural convection has been done. The results of the experiment show that the framing structure of BIPV under natural convection does not contribute to the temperature reduction of photovoltaic module cells. The temperature at the boundaries and the velocity profiles are used to create and validate CFD numerical models [13].

Acknowledgement

The current ongoing research work is supported by the Solar Building Research Network, a NSERC Strategic Research Network. A special thank to the Solar Calorimetry Laboratory at Queen’s University (Ontario) and the Department of Building, Civil, and Environmental Engineering at Concordia University (Quebec) for hosting the research work.

Nomenclature

Symbols Definition

A Cross section area of the duct (m2) L Thickness of bottom insulation (m)

duct oms

C Specific heat at bulk mean air L Thickness of side insulation (m)

p sin s

T Ambient air temperature (K)

References

[1] Benemann, J., Oussama, C., Schaar-Grabriel, E., 2001. Building integrated PV modules. Solar

Energy Material and Solar Cells 67, 345- 354

[2] Sartori E., 2006. Convection coefficient equations for forced air flow over flat surfaces. Solar Energy

80, 1063-1071.

[3] Brinkworth B. J., Sandberg M. 2006. Design procedure for cooling ducts to minimise efficiency loss

due to temperature rise in PV arrays. Solar energy 80, 89 -103

[4] Lin Q, Harrison S. J.: Experimental Study of Natural Convection in Asymmetrically Heated Inclined

Channel with Radiation Exchange. Proc. HT2003, ASME Summer Heat Transfer Conference, July 21-23, 2003, Las Vegas, Nevada, USA

[5] Liao, L., Athienitis, A. K., Candanedo, L., Park, K-W., Poisant, Y., and Collins, M. 2007: Numerical and Experimental Study of Heat Transfer in a BIPV-Thermal System. ASME Journal of Solar Energy Engineering, Volume 129, Issue 4, pp. 423-430.

[6] Brinkworth, B. J., Sandberg, M., 2005. A validated procedure for determining the buoyancy — induced flow in ducts. Building Services Eng. Res. Technol. 26, 35-48.

[7] Brinkworth B. J., 2000. Estimation of Flow and Heat Transfer for the Design of PV Cooling Ducts. Solar Energy 69 (5).

[8] Dascalaki, E., Santamouris, M., Argiriou, A., Helmis, C., Asimakopoulos, D. N., Papadopoulos, K., Soilemes, A., 1996. The combination of air velocity and flow measurements in single side natural ventilation configurations. Energy and Building 24, 155-165

[9] Moran M. J, Shapiro H,.N., 2002. Fundamentals of Engineering Thermodynamics. 5th edition, Wiley John Wiley & Sons, Inc.

[10] Kreith F., 1997. The CRC Hand book of Mechanical Engineering, Chapters: 2-4 and 9, CRC Press London.

[11] Tsuji T., Nagano Y. 1988. Characteristics of a turbulent natural convection boundary layer along a vertical flat plate. International Journal of Heat and Mass Transfer 31, 1723-1734.

[12] Smolec, W., Thomas, A., 1994. Problems encountered in heat transfer studies of Trombe wall. Energy Conversion and Management 35, 483-491.

[13] Candanedo L, Diarra C, Athinietis A, and Harrison S. 2008: Numerical modelling of heat and fluid flow in an asymmetri-cally heated tilted channel, 3 Canadian Solar Building Conference. Fredericton-New.

Canada decided to investigate air as the transfer medium to remove heat from PV arrays, represented by Conserval’s SolarWall transpired solar collector, while most of the European members focused on liquid heat removal. Rather than develop a new PV thermal panel, Conserval took the approach of combining commercially available PV modules on top of the transpired collector and utilizing the unique air balancing features of the transpired collector to remove heat from the back of the PV array. In essence, the PV panel becomes a back pass solar air collector with the PV cells acting as the solar heat absorber with ambient air passing around and behind each PV module, removing heat and then the heated air enters the perforations in the transpired panel. This concept allows for heat removal from most PV modules currently available on the market and avoids the lengthy delays associated with developing a new PV panel and obtaining the associated electrical approvals.

The trend in PV installations has been to use larger PV modules. To obtain data that is representative of the PV systems currently being installed, popular models from three manufacturers were chosen. It is realized that the thermal performance may not be optimized but the objective was to determine the amount of heat that could be recovered from these readily available modules.

Two test labs participated in the PV thermal air tests, Canada’s National Solar Test Facility (NSTF) located in Mississauga Ontario and the Danish Technological Institute (DTI) located in Taastrup Denmark.

Control strategy is fundamental in managing such a large and complex plant as it determines how the single machines get involved in the operation of the overall system. For this purpose several PID and on/off controllers have been included in the selected layout. The most significant of them are committed to control the variable speed pumps (VP in Fig. 4.) which regulate the mass flow in each component, except the cogenerator where a fixed mass flow is imposed. The goal is to supply heat and
cold energy flows at constant and unique selected values. E. g. a PID controller regulates the mass flow in the primary solar loop in order to reach the winter/summer set temperatures (VP S1 in Fig. 4.), or the hot mass flow entering the generator of the absorption chiller is regulated in order to provide chilling water at the temperature requested by the users (VP H in Fig. 4.).

Further important control devices are the diverters (Div H and Div C in Fig. 4.) which deliver the flows to the single units according to the following hierarchies: solar tank, cogenerator tank and biomass boiler on the hot side, absorption chiller and compression chiller on the cold side; it has to be highlighted that the temperature of the hot storage tanks are checked by means of on/off controllers before they get involved in the operation.