Метод, который наиболее часто используется при градуировке под: естественным солнечным излучением на поверхности Земли (как правило, в высокогорных условиях), заключается в экстраполяции результатов измерений к нулевой атмосферной массе [431]. При градуировке последовательно измеряют ток короткого замыкания эталонных солнечных элементов для различных значений атмосфер­ной массы (разная высота Солнца). Поскольку работа проводится в стационарных условиях, достаточно знать зависимость тока корот­кого замыкания эталонов от относительных значений атмосферной массы. Внеатмосферное значение тока короткого замыкания солнеч­ных элементов получают путем линейной экстраполяции зависимости логарифма тока от относительной атмосферной массы к ее нулевому значению.

Практически метод осуществляется путем измерения тока корот­кого замыкания эталонных элементов в течение половины солнеч­ного дня. Логарифмы измеренных значений тока наносятся на гра­фик в функции атмосферной массы, через экспериментальные точки проводится прямая линия (так называемая прямая Бугера), кото­рая линейно экстраполируется к значению тока при нулевой атмо­сферной массе. Строго говоря, зависимость логарифма тока корот­кого замыкания от атмосферной массы оказывается линейной только для монохроматического света. Так как кремниевый солнечный эле­мент чувствителен в достаточно широкой области спектра, то вслед­ствие эффекта Форбса эта функция изображается слабо вогнутой кривой. Однако при градуировке экстраполяцию проводят линейно, а затем вносят поправку на эффект Форбса [432]. Для вычислении

поправки (зпачение которой находится в пределах 1—3%) необхо­димо знать спектральное распределение коэффициента прозрачности атмосферы в течение всего периода градуировки эталонных эле­ментов.

Градуировка проводится в сухих горных районах, где выше про­зрачность атмосферы и для которых в определенные периоды года. характерна устойчивость оптических свойств атмосферы. Контроль •стабильности оптических свойств осуществляется по солнечному ореолу. При градуировке оптические свойства атмосферы считаются леизменными для промежутка времени, в течение которого значе­ние относительного солнечного ореола, рассчитанное на единицу ат­мосферной массы, изменяется немонотонно и в пределах, не пре­вышающих 10%.

Такой метод градуировки основан на законах атмосферной опти­ки [371—376, 433, 434]. Световой луч, проходя сквозь земную ат­мосферу, теряет свою интенсивность в связи с рассеянием и погло­щением. Согласно закону Бугера, отношение спектральной энергети­ческой плотности солнечного излучения на поверхности Земли Е% и вне атмосферы Е0х определяется ранее приведенным уравнени­ем (4.4).

Абсолютная атмосферная масса является функцией не только положения Солнца над горизонтом, но и высоты места над уровнем моря, что учтено введением в формулу (4.1) для определения атмо­сферной массы множителя р/р0 При малой высоте Солнца в расче­тах приходится использовать поправки, связанные с искажениями и оптическом пути лучей, вносимыми кривизной Земли и концентри­ческих слоев атмосферы, а также с искривлением солнечных лучей из-за постепенного и непрерывного изменения показателя прелом­ления воздуха по высоте. Точные значения атмосферной массы опре­деляют по таблицам Бемпорада [371] или таблицам, приведенным в монографии [373].

Обозначим в формуле (4.4) ехр(— а*) через Рх. Тогда закон Бу­гера для атмосферы принимает вид

Ек/Еок = Р£.

Введенная величина Рх называется спектральным коэффициен­том прозрачности земной атмосферы. Учитывая соотношение (4.5), выражение для тока короткого замыкания эталонного элемента на поверхности Земли можно представить следующим образом:

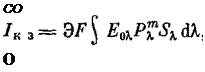(4.6)

где SK — спектральная чувствительность; F — площадь эталонного элемента; Э — коэффициент, учитывающий эллиптичность орбиты Земли и равный отношению энергетической облученности в данной точке орбиты к солнечной постоянной.

Поскольку ток короткого замыкания эталонного элемента при солнечной постоянной определяется выражением

Iamq== F j dX,
о

из уравнений (4.6.) и (4.7) можно получить

оо оо

/к 3= Э/д. мо§ E0xP™S^ dX J § ЕqxSі dX.

о ‘ о

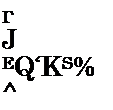Отношение интегралов в выражении (4.8) имеет смысл интеграль­ного коэффициента пропускания атмосферы:

Величина Рэф является эффективным коэффициентом прозрачно­сти атмосферы. Подставив соотношение (4.9) в выражение (4.8) и прологарифмировав, получим

lg Э/амо = lg І* з — т lg Рэф. (4.10)

Уравнение (4.10) используется для определения /амо путем гра­фической экстраполяции. На полученное таким образом значение тока накладывается поправка г|э [432], связанная с эффектом Форб­са [434]. Она определяется значениями эффективного коэффициента прозрачности Рэф в начальный (абсолютная масса тх) и конечный (т2) моменты измерений при стабильных параметрах атмосферы:

i|)=1+0,384 {т^+т^+Атм) (lg РЭф (тт) — lg Рэф (mi)) / (m2—mt).

(4.11)

Эффективный коэффициент прозрачности атмосферы РЭф можно определить исходя из следующих соображений. Согласно выраже­нию (4.10) для монохроматического излучения получаем

lgA = lg9Wo + «lg/V (4.12)

В данном случае Р не зависит от тп. Из уравнения (4.12) вид­но, что спектральный коэффициент прозрачности атмосферы Рк равен антилогарифму углового коэффициента прямой, изображаю­щей зависимость IgA от атмосферной массы. Таким образом, изме­рив ток короткого замыкания эталонного элемента при воздействии узкого, практически монохроматического излучения в условиях раз­личных атмосферных масс, можно получить значение спектрального коэффициента прозрачности для данной длины волны. Определив Р% во всем диапазоне излучения Солнца, где эталонный элемент из дан­ного полупроводникового материала чувствителен, по формуле (4.9) можем определить эффективный коэффициент прозрачности атмо­сферы Рэф.

Градуировка эталонных солнечных элементов проводится в СССР с 1965 г. регулярно один—три раза в год [394, 395, 418, 419, 430— 433] в окрестностях г. Алма-Аты на высокогорной станции Госу­дарственного астрономического института им. П. К. Штернберга (43° с. ш., 77° в. д., 3014 м над уровнем моря), сотрудниками ко­торого во главе с Э. В. Кононовичем создана программа расчета тока /кз эталонов на ЭВМ и оборудован солнечный телескоп для этих измерений. Во Всесоюзном научно-исследовательском институ­те источников тока В. Я. Ковальским с сотрудниками были раз­работаны аппаратура и методика проведения высокогорной гра­дуировки.

Относительная атмосферная масса М является функцией истин­ного времени т и зависит от склонения Солнца б на данный день и широты места наблюдений ф:

М= cosec 0=sin ф sin 6+COS ф cos б cos т,

где 0 — высота Солнца над горизонтом.

Отсчет моментов измерений при градуировке проводится ПО ДЄ-1 кретному времени Гд. Истинное время определяется по следующей формуле:

т=Гд—h—П+£>—Ат—12,

где П — часовой пояс места наблюдения; D — долгота места наблю­дения; Ат — уравнение времени (разница между средним и истинным временем); h — разница между поясным и декретным временем.

В результате расчетов получается зависимость относительной ат­мосферной массы от декретного времени.

Для каждого момента измерений тока короткого замыкания фоточувствительного элемента ореольного фотометра /ор (при наве­дении на ореол вокруг Солнца) и /с (при наведении непосредственно на Солнце) находится значение относительной атмосферной массы. Вычисляются значения относительного солнечного ореола Ос, рас­считанного на единицу атмосферной массы:

Oq = IopfIcm.

Определяется степень стабильности относительного солнечного ореола за половину солнечного дня. Находится интервал атмосфер­ных масс, при котором Ос изменяется немонотонно и в пределах, не превышающих 10%. В результате получается начальное и конеч­ное значения интервала атмосферных масс тгь и тп2 периода стабиль­ной атмосферы.

Пример определения /амо рассмотренным методом для двух эта­лонных элементов приведен на рис. 4.15.

Для вычисления поправки Форбса строится зависимость 1 g/*.= =/(m), где Д —значение тока короткого замыкания фильтрового монохроматора при различной атмосферной массе. Угол наклона

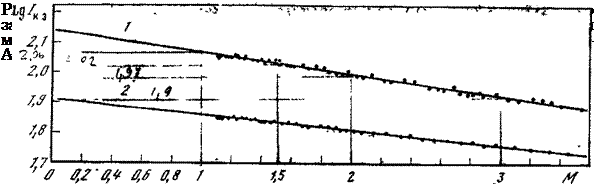1 — кремниевый; 2 — на основе гетероперехода АШаАа—GaAs

этой прямой к дает значение спектрального коэффициента прозрач­ности атмосферы Рх:

tg%=-lgPx.

Рассчитав Рх для всех фильтров, можно построить полную кри­вую спектрального распределения прозрачности атмосферы.

Эффективный коэффициент прозрачности атмосферы РЭф подсчи­тывается при начальном (тt) и конечном (т2) значениях интер­вала атмосферной массы периода стабильной атмосферы по форму­ле (4.9), а поправка на эффект Форбса ф —по формуле (4.11).

Окончательный результат градуировки — ток 1Амот, вычисляется по полученному значению тока для внеатмосферных условий /амо, •определенного экстраполяцией к нулевой атмосферной массе lg/m=o •с учетом поправок на эффект Форбса и на эллиптичность орбиты Земли:

/АМ0т = /тг=оф/Э.

Коэффициент эллиптичности орбиты вычисляется по отношению энергетической облученности на границе атмосферы в данной точке орбиты Земли к солнечной постоянной, т. е. к энергетической облу­ченности на среднем расстоянии от Земли до Солнца. Коэффици­ент Э в течение года меняется от 0,965 до 1,035; значение Э в кон­кретный день измерений берется из астрономического ежегодни­ка [435].