15.07.2015   EuroSun2008-11

Numerical results

The described sensitivity analysis methods are implemented into the Genopt (Generic optimization program) [4] and coupled with the simulation program TRNSYS. For the first system, the influence of 16 parameters on the target function, describing the overall cost of the system in ct/kWhsolar, was investigated by the Morris method. Results of the analysis are presented in the Table 1.

Table 1. Ranking of the parameters by their influence on the cost target function by the Moris method. The
value of the mean /и estimates the overall influence of the parameter and the deviation a shows its non-linear

effect.

N

Parameter

Variation range

и

5

1

^dis, max

Max. discharge spec. volume flow

[10; 15] in L/m2h

4.54

7.44

2

vsol, p

Specific volume flow

[6; 10] in L/m2h

2.29

2.92

3

Dvive

Pipe deameter

[20; 30] in mm

1.85

4.75

4

Vstore

Volume of solar storage

[4000; 8000] in Liter

0.46

0.58

5

Aon

Collector slope

[30; 46] in o

0.70

0.51

6

^Thyst

Hyst. for contr. pump in sec. circ

[1; 7] in K

0.41

0.29

7

Hch1

Rel. pos. of inlet 1

[0.6; 1]

0.30

0.77

8

Hch2

Rel. pos. of inlet 2

[0.1; 0.6]

0.24

0.21

9

Sh1

Rel. pos. of temp. sensor 1

[0.1; 0.5]

0.23

0.41

10

ATU

Temp. diff. to switch off the pump

[0; 7] in K

0.16

0.23

11

Sh2

Rel. pos. of temp. sensor 2

[0.55; 0.75]

0.18

0.26

12

UAshe

UA value of the sol. heat exch.

[70; 130] in W/m2K

0.08

0.09

13

У coll

Scaling factor

[-5; 6] in o

0.03

0.02

14

Ghyst

Hyst. for contr. pump in sol. circ.

[2; 50] in W/m2

0.02

0.02

15

Amin

Switch-off threshold for pump

[40; 200] in W/m2

0.01

0.02

16

Sh3

Rel. pos. of temp. sensor 3

[0.8; 1]

0.00

0.00

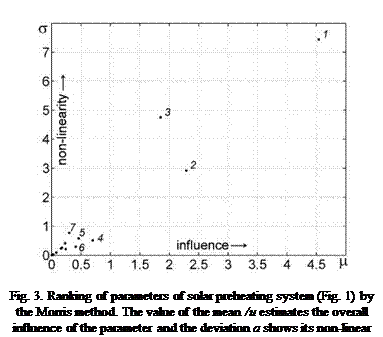
In Fig. 3 the mean и of the distribution G; versus the standard deviation a of the distribution F is given. The larger the value of the mean и. the larger the overall influence of the parameter. Large values of the standard deviation a mean strong non-linear effect of the parameter or its interaction with other parameters. It is seen that parameters 1-3 (the maximal power of two pumps in charging and discharging circuits and the diameter of pipes) are the most important and influence the target function both linearly and non-linearly. Parameters 4-7 could be considered as average important and the other 9 parameters as not important.

image285 Подпись: (4)

The second system has been investigated with the FAST. The target function is chosen as the fractional thermal energy savings :

Подпись: Table 2. Sensitivity of parameters of the reference system determined with the FAST algorithm. Parameter Variation range Test 1 Collector area [20; 100] in m2 0.8144 Store volume [3; 20] in m3 0.0776 Store UA value [0; 50] in W/K/m2 0.0732 Set temperature of DHW [40; 65] in °C 0.0012 Mass flow in solar loop [10; 70] in kg/h-m2 0.0272 Auxiliary volume [0.2; 1.0] in m3 0.0029

Table 2 shows the main effects on /avthenn of six parameters that were chosen by hand. The parameters have been changed in the given ranges. As the first test shows. the most influential parameter is the collector area (around 80% of all variation of /savtherm). In tests 2-4 the collector area is fixed at corresponding values and the importance of the other parameters is investigated. It is seen that the influence of the store volume and the mass flow grows with increasing the collector area.

Sensitivity indices (main effect)

Test 2

Test 3

Test 4

Fixed at 30 m2

Fixed at 50 m2

Fixed at 100 m’

0.2780

0.3823

0.5655

0.5856

0.4370

0.2630

0.0215

0.0140

0.0083

0.1136

0.1328

0.1353

0.0100

0.0090

0.0094

4. Conclusion

The sensitivity analysis methods applied to the solar heating systems show that only some parameters have significant influence on the corresponding target functions. If the target function depends on many system parameters and only the most influential parameters should be identified then it seems to be computationally more efficient first to apply the Morris method and then the FAST algorithm.

Nomenclature

Dme

mm

diameter of pipes

d,

—

Elementary effect

Eaux

kWh

Auxiliary final energy consumption of the solar combisystem

Eref

kWh

Final energy consumption of the reference system

E( y x)

—

expectation of the target function y conditional on a fixed value of parameter x

F

—

Distribution of elementary effects

./s&v, therm

—

Fractional thermal energy savings

G

—

Distribution of absolute values of elementary effects

Gmm

W/m2

Switch-off threshold for controlling the pump in the solar circuit

Ghyst

W/m2

Hysteresis for controlling the pump in the solar circuit

Hch1

—

Relative position of the inlet charging the hot store.

Hch2

—

Relative position of the inlet charging the cold store.

K

—

transformation functions

S

—

Main effects

s

—

Scalar variable

Sh1-Sh3

—

Relative positions of the temperature sensors for switching on the solar circuit.

UASHE

W/m2K

UA value of the heat exchanger in the solar circuit

Varx,

—

variation taken over all possible values of x

V.-

dis, max

L/m2h

Maximal discharge specific volume flow

v> і

sol, p

L/m2h

Specific volume flow in the primary solar circuit

Tstore

Liter

Volume of solar storage

x

—

Parameters vector

y

—

Target function

Fcoll

o

Collector slope

Ycoll

o

Scaling factor

A

—

Displacement

AT.

K

Temperature difference for switching off the pump in the secondary solar circuit

AThyst

K

Hysteresis for controlling the pump in secondary solar circuit

M

—

mean of the distribution G

a — deviation of the distribution F

wi — Angular frequency

References

[1] A. Saltelli. S. Tarantola. K. Chan. Technometrics. 41(1) (1999). 39-56

[2] A. Saltelli. S. Tarantola. F. Campolongo. M. Ratto. (2004). Sensitivity Analysis in Practice. A Guide to Assessing Scientific Models. John Wiley & Sons publishers

[3] M. Krause. K. Vajen. F. Wiese. H. Ackermann. Solar Energy 73 (4) (2003). 217-225

[4] GenOpt. Generic Optimization Program. http://gundog. lbl. gov/GO/