Как выбрать гостиницу для кошек
14 декабря, 2021
The system is modeled and simulated with TRNSYS and the typical meteorological year (TMY) of Nicosia, Cyprus. In this section both TRNSYS and TMY are shortly presented and details of the model are given.
3.1 TRNSYS Program Description
TRNSYS is an acronym for a “transient simulation program” and is a quasi-steady simulation model [3]. The program consists of many subroutines that model subsystem components. The mathematical models for the subsystem components are given in terms of their ordinary differential or algebraic equations. With a program such as TRNSYS, which has the capability of interconnecting system components in any desired manner, solving differential equations and facilitating information output, the entire problem of system simulation reduces to a problem of identifying all the components that comprise the particular system and connecting them together to form the complete system model.
The latest version of TRNSYS (version 16) works in a graphic interface environment called the simulation studio. In this environment, icons of readymade components are dragged and dropped from a list and connected together according to the real system configuration. Each icon represents the detailed program of each component of the system and requires a set of inputs (from other components or data files) and a set of constant parameters, which are specified by the user. Each component has its own set of output parameters, which can be saved in a file, plotted, or used as input in other components. Thus, once all the components of the system have been identified and as the mathematical description of each component is readily available, the user all he has to do is to construct an information flow diagram for the system, the purpose of which is to facilitate identification of the components and the flow of information between them. The flow diagram also contains information on the weather data file and the output format.
TRNSYS is employing the standard second-order collector performance equation to model the collector, given by:
(T — Ta) (T — Ta )2
where kaT is the incidence angle modifier given by:
The values of c0, cb c2 and bo are obtained by experimental testing of collectors in accredited laboratories. The values employed in the present system are shown in Table 1. The useful energy extracted from the collectors is given by:
ft = FAKtTG — ft ( — Г, )] (3)
The total useful energy for the whole year is obtained from:
365 24
![]()
Q„,a = YY. Q.
d=1 h=1
and the auxiliary energy required, Qaux is:
where Qload is the energy required by the load, Qloss is the energy lost from the storage tank and pipes and Qrei is the energy relieved from the storage tank relief valve.
As can be seen from the above equations the energy obtained from the solar collector field depends on the collector area (A), collector slope (affects cos0), flow rate (affects FR) and the storage tank size (affects Ti). The collector inlet temperature depends also on the load pattern, make-up water temperature, the losses from the storage tank and pipes and the energy relieved from the relief valve. The storage tank losses and energy relieved from relief valve depend on the temperature of the stored water, i. e., it depends on the energy collected and storage tank size.
The system presented in this paper is simulated with TRNSYS using Typical Meteorological Year (TMY) data for Nicosia, Cyprus. The selection of typical weather conditions for a given location is very crucial in computer simulations for performance predictions and has led various investigators either to run long periods of observational data or to select a particular year, which appears to be typical from several years of data. The TMY for Nicosia, Cyprus, was generated from hourly measurements, of solar irradiance (global and diffuse on horizontal surface), ambient temperature, wind speed and direction and humidity ratio, for a seven-year period, from 1986 to 1992 using the Filkenstein — Schafer statistical method [4]. The measurements were recorded by the Cyprus Meteorological Service at the Athalassa region, an area at the suburbs of the town of Nicosia. The TMY is considered as a representative year for the Cypriot environment.
TMY is defined as a year, which sums up all the climatic information characterizing a 30 year period record and not the operation lifetime of solar systems. Every about 10 years TMY files need updating to reflect climate changes, especially in cases where urbanization, pollution, increasing/decreasing of aerosols, drought, etc. takes place. Therefore an added advantage of the present method is that if this periodic updating of TMY fails to be done in regular intervals, some extreme effects can be accounted. Additionally, uncertainty in the weather patterns could include large-scale geophysical, human or nature caused events, like volcanic eruptions (Mt. Pinatubo eruption created aerosols which took two years to settle out), forest burning, increased storm occurrence, etc. which can have a much larger impact on short term and long-life system performance.
In this paper the effect of introducing uncertainty or noise in the weather data and load pattern is examined. The noise is introduced by using Type 578 (Random number generator). This model creates a random number drawn from a normal distribution based on user supplied values of the
mean (average) and standard deviation. For the parameters considered here these are shown in Table 3.
|
Table 3 Mean and standard deviation of the parameters considered in this work
|
It should be noted that higher values of radiation resulted in messages that the horizontal component of radiation is higher than the extraterrestrial value and that the latter will be used, as a maximum value.
For the ambient temperature the noisy value is added to the normal value using the equation component of TRNSYS as:
Ta, new Ta, normal + Ta, noisy (6)
For the case of solar radiation the following equation was used in order to avoid adding radiation in hours where the normal value is zero, i. e., during nighttime:
Radnew Radnormal+LT(0,Radnormal)*Radnoisy (7)
The term LT (0,Rad) is a standard TRNSYS function which returns 1 when Rad>0 and 0 when Rad=0. Similarly for the load demand:
DHW new=DHW normal+DHW noisy*LT(0,DHW normal) ( 8 )
This avoids adding demand at the hours where its value is zero (early in the morning, see Fig. 2).
It should be noted that this analysis could also be performed by specifying the mean or average values of the various parameters shown in Table 3, without the need of equations (6) to (8). In this case however, the introduction of negative values into the simulation would have been unavoidable.
3.2 System Simulation
The normal system simulation is carried out with the aid of TRNSYS and the TMY for Nicosia, Cyprus. The system is also simulated by introducing noise in various parameters as shown above.
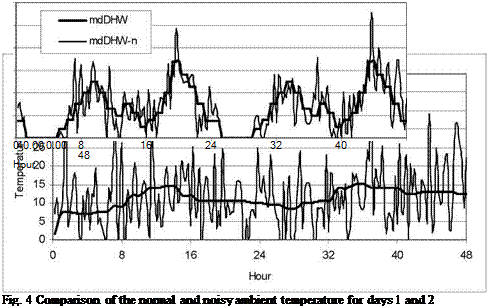
In all graphs that follow the mark “n” in the various parameters represent the values corresponding to the operation with noisy conditions. Figures 3 and 4 show a comparison of the normal and noisy radiation and ambient temperature respectively as obtained from the program for the first two days of the year. Similarly, Fig. 5 show a comparison of the normal and noisy hot water consumption profile for the same period. As can be seen the radiation values are not affected significantly whereas both ambient temperature and demand profile show large variations. It can also be seen that the noise is different from day to day, it is however impractical to show this variation for all days of the year.
A comparison of the annual performance of the normal (without noise) and noisy systems is shown in Table 4. As can be seen the annual differences are minimal which means that the noise introduced as described above has not created large differences. The solar energy incident on the
 |
collector is very much the same whereas the greatest difference is for the auxiliary energy which for the noisy system is reduced by 6.3%.
Fig. 5 Comparison of the normal and noisy hot water consumption profile for days 1 and 2
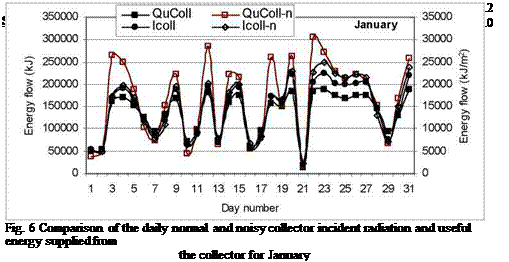
Of course the differences on a daily basis are expected to be more significant and these are presented and analyzed below. As it is impractical to show a comparison for all months of the year only January and July are presented showing typical winter and summer performance respectively.
 |
|
As can be seen from Figs. 6 and 8, in both January and July, although the difference in the total radiation falling on the collector is not much there is considerable difference in the useful energy supplied from solar collectors.
|
January A jy’AsA’^A. a. Ay |
||
|
1 |
3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 Day number |
|
250000 200000 150000 |
|
Fig. 7 Comparison of the daily normal and noisy domestic hot water load and auxiliary energy supplied from the collector for January |
Also as shown in Figs. 7 and 9 for January and July respectively, the hot water load for the nonnoisy case is almost constant and much larger for the noisy case, but this has almost a negligible effect on the auxiliary energy required during the summer period and a more pronounced effect during the winter, as both the makeup water temperature replacing the demand and the performance of the solar system during this period are much lower.
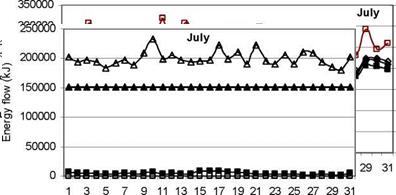 |
Fig. 9 Comparison of the daily normal and noisy domestic hot water load and auxiliary energy supplied from
the collector for July
2. CONCLUSIONS
As it is proved in this paper annual performance of the system is not very much different compared to the normal non-noisy model whereas the daily and hourly performance shows some considerable variations. It is believed that the present method gives more reliable results to the long-term performance evaluation of the systems and should be followed once the optimum system is obtained as it produces more reliable results. This is more important in cases where guaranteed solar results schemes are followed where possible mistakes could result in significant penalties.
References
[1] Kalogirou, S., The potential of solar industrial process heat applications, Applied Energy, 76 (2003) 337-361.
[2] Kalogirou, S., Optimisation of solar systems using artificial neural networks and genetic algorithms, Applied Energy, 77 (2004) 383-405.
[3] Klein S. A., et al. (2004) TRNSYS program manual, University of Wisconsin.
[4] Kalogirou, S., Generation of typical meteorological year (TMY-2) for Nicosia, Cyprus, Renewable Energy,
28 (2003) 2317-2334.