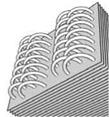
The energy equations related to the adsorber, which will be given next, correspond to a multi-tubular system, whose inner surface exchanges heat with the water coming from the hot storage tank or from the water supply network, depending on the stage of the cycle. The adsorbent occupies the space delimited by the external wall of the tube and the corrugated fins.

Fig. 2 — Fin-tube heat exchanger and the simplification by annular fins

For the heat transfer in the adsorbent medium, the following model assumptions have been considered: (a) the pressure is uniform; (b) the heat conduction is two-dimensional (axial and radial) as detailed in Fig. 2; (c) the adsorbent-adsorbate pair is treated as a continuous medium in relation to thermal conduction; (d) the convective effects and pressure drops are negligible; (e) the condenser and evaporator are ideal, i. e. they have a constant temperature during the isobaric phases; (f) all the adsorbent particles have the same properties (including shape and size); they are uniformly distributed throughout the adsorbent, and in local thermal equilibrium with the adsorbate and the surrounding gaseous phase; (g) the gaseous phase behaves as an ideal gas; (h) the properties of the metal and the gaseous phase are assumed to be constant; (i) the properties of the heat transfer fluid, as well as those of the adsorbate, are considered as temperature dependent. It results the following equation

[Pi (CPі + aCP2 )] ] = к V2T + qst p ^ (2)

d t d t

where Cp is the specific heat (indices 1 and 2 refer to the adsorbent and the adsorbate, respectively), p the specific mass and к, the conductivity of the adsorbent. The total derivation of the concentration, a, is given by

The da/dt term depends on the process that occurs in the adsorber. In the case of an isosteric process it is zero and for adsorption or desorption process, the term d lnp/dt is zero. Then, the energy equation for the adsorbent can be written as

where u is a function of the process, 0 for isosteric and 1 for adsorption or desorption process. The condition in the middle of the adsorbent material, between two fins or two tubes comprises the adiabatic boundary condition. Other boundary conditions are in the interface between the adsorbent and the wall of the tubes and the fins. To solve the Eq. (4), the temperature on the wall of the tubes and on the fins are considered known, recalculated for each simulation step by the energy equation

to the tubes and the following to the fins

where P is the perimeter, A is the area, Tt is the tube temperature, Tw is the water temperature, h is the conductance at the interface tube/adsorbent, and hfi is heat coefficients between the fluid and the tubes. The hfi is evaluated as the method described in [3]. The boundary conditions of Eq. (5) are adiabatic in both extremities and, to Eq. (6), they are adiabatic in the middle of the fin and known in the interface tube/fin. The temperature of the water is given by

were mw is the mass flow of water. To solve the system of equations formed by Eq. (1), (4), (5), (6) and (7) a mixed finite-difference and finite-volume method was used and the input data is chosen to be the temperature and the mass flow of the hot water, the number of tubes, the number and the thickness of the fins and the material of the fin. Additionally, the porous medium properties must be known, especially к and h. According to [4], for the AC-35 activated carbon: к = 0.19 W/mK and h = 16.5 W/m2K.