An energy balance is applied in each node and is represented by a network thermal resistance as we can see in Figure 2.

 

T 1 T я.

 

Fig. 2. Thermal network for the solar chimney.

 

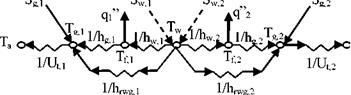
Following the methodology reported by Ong [7] and Duffie and Beckman [8], the energy balances produce a system of 5 algebraic equations, and such equations can be expressed as the following array (1):

Where column [Tg, b Tg,2, Tw, Tf, b and Tf2], is the unknown temperature vector. It represents the both glass cover temperatures, the metallic vertical plate temperature, and both air fluid temperatures respectively.

The temperature vector is calculated by solving the matrix system. All the heat transfer coefficients are determined from the literature references, as well as the optical properties for the materials, Table 1 shows these values.

Table 1. Optical properties for the materials [9]. Material emissivity absortivity Transmissivity Glass cover 1 0.83 0.06 0.84 Glass cover 2 0.83 0.06 0.84 Black paint 1 0.91 0.95 0.0 Black paint 2 0.91 0.95 0.0

Where every coefficient is defined in the nomenclature, for i = 1, channel one, and for i = 2, channel two. The convective heat transfer coefficients for natural convection, are determined after applying the Nusselt correlation, for laminar flow, equation (2), for turbulent flow, equation (3),

[10] .

Nut = 0.68 + (0.67Ra.025)/[1 + 80.492/Pr)9/16J/9 Ral < 109,

N. = {0.825 + (0.387Ra 11<5)/[1 + (0.492/Pr)9/16fmf Ra > 109,

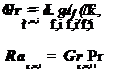Prandtl number, Rayleigh number, and Grashof number are defined by equations (4), (5) and (6) respectively.

The volumetric coefficient of expansion /3, is defined by equation (7), and it is evaluated at a mean temperature by equation (8). All thermophysical properties are evaluated at T.

Pf, t = 1/Tm„ , IS (1/K) T + T )

g,1 w, t

2

The top loss coefficient and the wind heat transfer coefficient are evaluated by equations (9) and (10), respectively, where V, is the wind velocity in (m/s).

h = 5.7 + 3.8V

The radiation heat transfer coefficient from the glass cover to the sky, is evaluated by equation

(11) , where T is the sky temperature, defined by equation (12).

h = os (T + T)(T2 + T2)(T — T)/(T — T )

rs, t g ,t g, t s g, t s g, t s g ,t a, t

T = 0.0552 Г5 (12)

The solar irradiance covering the glazing, and the transmitted solar irradiance covering the metallic plate, at both sides, are defined by equations (13) and (14), respectively.

sg, t = ag, tG (13)

S =t a G (14)

w, t g, t w, t

It is convenient to defined an aspect ratio At and a theoretical parameter Mt by equations (15) and (16) respectively.

The mass flow rate through each channel of the solar chimney was determined by using an equation proposed by Bansal et al., [11], equation (19).

РоЛл l2SLc fat — T )

л,/1+а;д

The thermal efficiency was determined using the following equation, (20), [7]

m c, ІТ — T )

n = GG *100

WLG