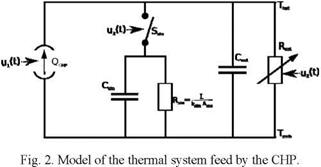The high overall efficiency of cogeneration plants is a result of the simultaneous production of electricity and heat. This effect only is valid if both products can be used. The heat only can be used in the local heat system or stored for a later use. For that reason it is important to model the thermal system. To model the thermal system it is useful to transform the equations into a thermal equivalent circuit (Fig. 2).

The CHP can be seen as a current source QCHP which is modulated control variable ui(t). The fed thermal network is represented by a variable resistance Rnet, which is controlled by u2(t), and a capacity Cnet, which represents the thermal capacity by changing the temperature level in the allowed range. The usage of the thermal storage is necessary if Cnet is used completely and the CHP should operate anyway, e. g. in case of high feed-in tariffs. The switch Ssto, controlled by u3(t), represents the valve regulating the liquid flow through the storage. The storage is modelled as a capacity Csto and a parallel resistance Rsto = k 1Arepresenting the heat losses to the ambience. The thermal conductivity is given

by kstoAsto. In this model all temperatures are referred to the ambient Tamb. This also can be written as differential equation:

The three input variables u1(t), u2(t), u3(t) define the output of system described before. It is assumed that Thot stays above 60 °C. For the simulation the thermal demand is given as a time series and defines u3(t). In the showcase it is not possible to modulate the CHP, so u1(t) can have the discrete values 0 and 1. To optimise the operation of the CHP the best relation of u1(t) and u3(t) according objective function must be evaluated. The target of the system operator is to minimise his operation costs. It is assumed that the CHP can fed into the electricity grid with a variable tariff cel(t) anytime. This directly influences the operation costs c(t) of the system. Neglecting heat storage losses, the operation costs depend on the feed-in tariff cel(t) and the fuel costs cfuel. The objective function can be defined as:

Jc(t) = J u Шшр [иеі -4elcd (t)]= mm (2)

t t nth

The used primary energy can be calculated with the thermal efficiency nth of the CHP. The variable nth/hei defines the ratio between produced heat and electricity. Nonlinear relations like the discrete operation of the CHP, the given time series for cel(t) and the thermal demand make an analytic solving very complex. To reduce the complexity we made linear approximations and transformed the problem to a mixed integer linear problem MILP [4]. These kinds of problems have got the advantage that their performance still with a high number of variables is very good. There are also efficient solvers with the Simplex algorithm available [5].