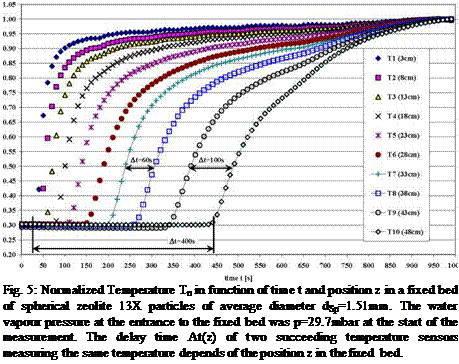
In Fig. 4 the normalized temperature Tn=T(t)/Tmax development in function of time t in a fixed bed of spherical zeolite 13X particles of average diameter dp=1.51mm is shown. The direct correlation of T and p in the fixed bed sorption process was shown in Fig. 3. An increased time delay At can be seen in which two succeeding temperature sensors in the equally spaced array of distance l=5cm are measuring the same temperature values. For example the time delay At=[t(T8)-t(T7)]=250s or At=[t(T10)-t(T9)]=500s can be measured for the normalized temperature of Tn=0.5 at the sensor T7 (z=33cm) and T8 (z=38cm) or T9 (z=43cm) and T10 (z=48 cm). These time delays are strongly dependent on the average particle diameter dp and the vapour pressure p(T) at the entrance to the sorption material fixed bed. For comparison in Fig. 5 the data for a pressure of p=29.7mbar i. e. the temperature T=25°C in the sorbate water tank, at the entrance to the same fixed bed are shown and a reduction of the time delay for Tn=0.5 to At=[t(T8)-t(T7)]=60s and At=[t(T10)-t(T9)]=100s can be seen.

time t [s] Fig. 4: Normalized Temperature Tn in function of time t and position z in a fixed bed of spherical zeolite 13X particles of average diameter dSp=1.51mm. The water vapour pressure at the entrance to the fixed bed was p=16.3mbar at the start of the measurement. The delay time At(z) of two succeeding temperature sensors measuring the same temperature depends of the position z in the fixed bed.

SHAPE * MERGEFORMAT

Fig. 5: Normalized Temperature Tn in function of time t and position z in a fixed bed of spherical zeolite 13X particles of average diameter dSp=1.51mm. The water vapour pressure at the entrance to the fixed bed was p=29.7mbar at the start of the measurement. The delay time At(z) of two succeeding temperature sensors measuring the same temperature depends of the position z in the fixed bed.

In Fig. 6 the time dependent development of the water temperature in the evaporator heat exchanger inlet T(HX in) and outlet T(HX out) are shown for a zeolite 13X fixed bed of dp=1.51mm a) and dp=2.63mm b) and a water inlet temperature of T(HX in)=25°C. After a time of t=200s to t=250s the minimum T(HX out) is reached and the temperature difference AT= T(HX in)-T(HX out)=3.5°C and AT=5.0°C are reached for the two particle size distributions. A linear temperature increase T(HX out) in the sorbate water tank is observed for adsorption process times longer than about t=300s.

0

тппптплпппппп □ □ о □ с О temperature T(HX out) temperature T(HX in) о AT= 5.0 °C «о**30 о o< ……………… «*** 0 50 100 150 200 250 300 350 400 450 500 550 600 time t [s]

300

In Fig. 7 the pressure p measurement in function of the position z and the time t is shown for the pressure sensors installed at the first z=28cm of the fixed bed. A linear dependence of the water vapour pressure p from the position z can be assigned. While the process time t is increasing the pressure gradient dp/dz in the fixed bed is decreasing. This effect is illustrated with the two lines a) and b). Two effects are contributing to this behaviour. The adsorption which in this zeolite 13X is governed through the Langmuir isotherm [13] is dominating as long the equilibrium concentration c(p, T) is not reached.

a) b)

Fig.6: water temperature T as a function of time t at the outlet T(HX out) and the inlet T(HX in) of the evaporator heat exchanger at the start temperature T(HX in)=25°C for a fixed bed with dp=1.51mm a) and a fixed bed with dp=2.63mm b). After a time of approximately t=200s the minimum of the outlet temperature T(HX out) in is reached and from there on a linear increase of the temperature T(HX out) can be observed.

Fig. 7: Pressure p development in function of the
position z in the fixed bed of spherical zeolite 13X
particles of average diameter dSp=1.51mm and water
vapour pressure p(T)=16.3mbar at the entrance to the
fixed bed. The curves with the parameter time t are
showing a linear dependence of the pressure p(z). A
transition from a higher pressure gradient a) to a lower
one can be seen b).

8 18 23 position z in the fixed bed [cm]

After the particles have reached the equilibrium concentration the water vapour flowing through

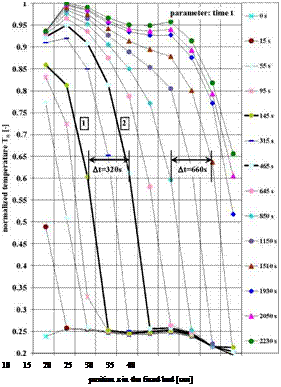
this region of the fixed bed undergoes the typical pressure drop a gas is subject to [14]. Calis [15] showed this in simulations for a validation of experimental results in a simplified model. The normalized temperature Tn in function of the position z is shown in Fig. 8 for a water vapour pressure of p(T)=16.3mbar at the entrance to the fixed bed and the average particle diameter dp=1.51mm and the parameter time t. The time delay At to measure the same normalized temperature Tn in two sensors at different positions z is increased for example from At=t(Tn, z=23cm)-t(Tn, z=13cm)=320s to At=t(Tn, z=43cm)-t(Tn, z=33cm)=660s. Thus the speed uT of the fixed bed traversing moving temperature front is decreased by the increasing length z of the fixed bed. From curve 1 and 2 in Fig. 8 the mass transfer zone length LMtZ can be measured to LMTZ=0.18m.

For the different inlet temperature levels of T(HX in)=15°C to 25°C and the average particle diameter dp=1.51mm and dp=2.63mm the temperature T(HX out) decrease reaches the minimum after

10 15 20 25 30 35 40 position z in the fixed bed [cm]

approximately t=200s to t=300s followed by a linear increase. The temperature difference AT development as a function of time indicates that the (cooling) power in the water tank reaches a maximum in the above mentioned time t.

Fig. 8: Normalized temperature Tn development as a
function of the position z in the fixed bed of spherical
zeolite 13X particles of average diameter dSp=1.51mm
and water vapour pressure p(T)=16.3mbar at the
entrance to the fixed bed. The curves with the parameter
time t are showing a moving temperature front through
the fixed bed and the speed uT of the front is depending
of the position z (see for example At=320s and At=660s).

To reach a high power of the closed sorption system an optimum of the fixed bed geometry related to the MTZ length can be determined for the sorbent — sorbate combination of a granular zeolite 13X sorbent material and a vapour phase sorbate. But this geometry limits the total energy output Qth of the system. In addition a power density of Pth/Afb =33kW/m2 was determined where the area A represents the cross section of the fixed bed. In the closed adsorption system with spherical zeolite 13X particles the length of the MTZ is LMTZ(dp=1.51mm)=0.18m and LMTZ(dp=2.63mm)=0.38m, respectively. And, in a closed sorption system with zeolite 13X — water as the sorbent — sorbate combination the cycle time of discharging and charging is in the range of 5 Min to 8 Min [5]. As a conclusion to the findings the closed fixed bed
storage system has a limited energy and power output determined by the sorbent — sorbate material combination and the granular structure of the sorbent i. e. the diameter dp of the particles.

Table 2. Summary of the experimental results. Temperature T(HX in) [°C] Pressure p(T) (sorbate tank) [mbar] 15 16.3 20 23.4 25 29.7 Particle diameter dp (av.) [mm] 1.51 2.63 1.51 2.63 1.51 2.63 hydraulic diameter dh [mm] 0.168 0.292 0.168 0.292 0.168 0.292 Time At to T10(t)>T10(t=0) [s] 1750 140 630 140 400 82 Average speed uT [mm/s] 0.27 3.43 0.76 3.43 1.20 5.85 Length of MTZ LMTZ [m] 0.18 0.38 0.18 0.38 0.18 0.38 Cooling power Pth/A [kW/m2] 15.1 21.0 16.4 22.0 16.4 33.0

Ap P

(1 — A

s

3

(3)

B

While the thermal power Pth of an adsorption system depends of the vapour mass m adsorbed in time multiplied by the heat of adsorption AhA(T, c), the vapour flow through a granular fixed bed undergoes a pressure drop Ap depending on the inverse of the hydraulic diameter dh. Ergun [14] proposed an equation for the pressure drop in a fixed bed. In equation (3) the normalized pressure drop Ap/p depending on the vapour flow velocity u in a fixed bed of length L depending of the particle Reynolds number Rep and pressure drop factors A and B is given [11]:

According to equation (3) the pressure drop is a linear function of the length L. Because of the direct correlation of the vapour pressure p to the mass m in a given volume V through the equation of the ideal gas a linear power drop in the sorption system will occur when vapour flows through a section of saturated particles in the fixed bed.

The energy output Qth of the closed sorption system is the integral of m (sorbent) * AhA(T, c) over the cycle time t, sorbate content c and temperature T. The diameter dp of the particle also determines the length of MTZ and the total reaction (macroscopic) surface on which the reaction (adsorption) takes place. The total adsorption surface AMTZ in the MTZ is the product of the number n of particles and their individual surface Ap=n*dp2. The power Pth of the sorption system is a function of the reaction surface Pth(AMTZ = LAp). So, by measuring the temperature T and pressure p in function of time t and position z in the fixed bed the dynamics of a closed sorption system can be better understood.

4. Conclusion

The length of the mass transfer zone LMTZ and its moving speed uT through the fixed bed depends of the pressure p(T) at the entrance to the fixed bed and the average particle diameter dp which determines the hydraulic diameter dh. The higher the pressure p(T) — the driving force — and the larger the hydraulic diameter the longer LMTZ and the higher uT. The sorption behaviour of the fixed bed can be explained by a quasi continuum particle model.

In a closed solid sorbent — vapour sorbate sorption system no pump or fan is transporting the vapour into the fixed bed. The external temperature level T(HX in) to the sorbate tank determines the vapour pressure p(T) in the tank and the average particle diameter dp determines the hydraulic diameter dh of the fixed bed. Therefore, beside the heat transfer from the solid sorbent to a heat exchanger, after the two components sorbent — sorbate and the temperature level i. e. the pressure level is determined, the thermal power Pth and the energy Qth output of a closed solid sorption system is limited through the fixed bed hydraulic diameter dh. And because the single particle is saturated in a few minutes the size
of a solid sorption heat storage system is limited by the sorbent fixed bed hydraulic diameter dh i. e the particle diameter dp.

The actual interpretation of the experimental results in the closed sorption system take also account of the findings presented in literature about open sorption or catalytic systems in which for example a gas is the heat and mass transporting fluid. And the setup of the presented sorption system is in principle a heat pump and so the results can be used for the development of hest pumps. The measurements are showing that a solid sorbent — gas/liquid sorption system is more suitable for heat pump or cooling machine applications rather than thermal storage systems. But further experiments for a better understanding of the dynamic behaviour of the closed sorption system fixed bed will be needed.

Nomenclature

General	Subscripts
L	length of the fixed bed, m	A	adsorption
z	position in the fixed bed, m	h	hydraulic
dp	particle diameter, mm	max	maximum (Tmax)
dh	hydraulic diameter, mm	MTZ	mass transfer zone
D	fixed bed diameter, mm	n	normalized (Tn=T(t)/Tmax)
uT	speed (dz/dt) of the temperature front in the	p	particle
	fixed bed, mm/s	T	temperature (uT)
V	volume, m3	th	thermal
f	particle shape factor (sphere f=1)	w	factor
Afb	fixed bed area Afb=n*D2/4, m2
Ap	particle surface Ap=n*dp2, m2	Greek letters
AMTZ	adsorption surface in MTZ AMTZ=n*n*dp2,	P	density
	m2	є	porosity
p	pressure, mbar	A	difference (heat of adsorption)
T	temperature, °C
c	concentration, kg/kg
m	mass, kg
m	water vapour mass flow, kg/s
u	water vapour velocity, m/s
Pth	power, thermal, kW
Qth	energy, thermal, kJ
AhA	heat of adsorption, kJ/kg
Re*	Reynold number
A, B	coefficients in Eq. (3)
t	time, s

Acknowledgements

Financial support of the Swiss Federal Office of Energy is gratefully acknowledged. The work was done under the IEA Task 32 Program and so special acknowledgment goes to the members of the IEA Task 32 group for very fruit full discussions. The author also would like to acknowledge F. Flueckiger who designed the data acquisition concept and W. Camenisch who did the welding of the laboratory vacuum equipment.

References

[1] Mittelbach, W. et al (2000), Solid sorption thermal energy storage for solar heating systems. TERRASTOCK 2000, Proceedings of the 8th International Conference on Thermal Energy Storage, Stuttgart Germany, Aug. 2000, 415-420.

[2] Purkarthofer, G., Sorptionsspeicher — Langzeitspeicherung von Warme mit hohen Energiedichten. SOLAR 2002, 6. Internationales Symposium fur Sonnenenergienutzung, Oktober 2002, 85-90.

[3] Stach, J. Mugele, J. Jaenchen, E. Weiler, Influence of the cycle temperature on the thermocemical heat storage densities in the systems water/microporous and water/mesoporous adsorbents. Adsorption 11: 393-404, 2005.

[4] Jaenchen J., D. Ackermann, H. Stach, W. Broesicke, Studies of water adsorption on zeolite and modified mesoporous materials for seasonal storage of solar heat. Solar Energy 76 (2004) 339-344.

[5] Gantenbein P., Adsorption speed and mass transfer zone analysis of water vapour on the solid sorbent materials zeolite and Silicagel with the focus on the heat exchanger design. ECOSTOCK 2006.

[6] Saha, B. B.; Boelman, E. C., and Kashiwagi, T. (1995), Computer simulation of a silica gel-water adsoption refrigeretion cycle — the influence of operating conditions on cooling output and COP. Technical and symposium papers. Annual meeting of the American Society of Heating, Refrigeration and Air-Conditioning Engineers, Inc. (ASHRAE Transactions); 24 June 1995 -28 June 1995. San Diego, CA. Atlanta, GA: American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc.; Vol. 101, Part 2, pp. 348-357.

[7] Boelman E. C., Saha, B. B.; Kashiwagi, T. (1995), Experimental investigation of a silica gel — water adsorption refrigeration cycle — the influence of operating conditions on cooling output and COP. ASHRAE Transactions, Vol. 101, part 2, 1995, p. 358.

[8] Boelman E. C., Saha, B. B.; Kashiwagi, T. (1997), Parametric study of a silica gel — water adsorption refrigeration cycle — the influence of thermal capacitance and heat exchanger UA-values on cooling capacity, power density, and COP. ASHRAE Transactions, Vol. 103, part 1, 1997, p. 139.

[9] Zeochem / Uetikon, private communication.

[10] VDI-Waermeatlas (1997), Recherchieren — Berechnen — Konstruieren. Herausgeber: Verein Deutscher Ingenieure, Springer Verlag Berlin Heidelberg.

[11] Keule F., Das Trocknen, Grundlagen der chemischen Technik, Verlag Sauerlander & Co. Aarau und Frankfurt am Main.

[12] Freund H., Zeiser T., Huber F., Klemm E., Brenner G., Durst F., Emig G., Numerical simulations of single phase reacting flows in randomly packed fixed-bed reactors and experimental validation. Chemical Engineering Science 58 (2003) 903 — 910.

[13] http://en. wikipedia. org/wiki/Adsorption & references therein.

[14] Ergun S., Fluid flow through packed columns, Chemical Engineering Progress Vol. 48 No. 2, 1952, 89­94.

[15] Calis H. P. A., Nijenhuis J., Paikert B. C., Dautzenberg F. M., Van den Bleek C. M., CFD modelling and experimental validation of pressure drop and flow profile in a novel structured catalytic reactor packing. Chemical Engineering Science 56 (2001) 1713 — 1720.