The subsequent simulation runs were carried out in order to calculate the best collector tilt angle for the thermosiphon system under the climatic conditions of Rome, a typical target region for thermosiphon systems. The goal behind these simulations was to achieve the best solar fraction even during winter times. The basis for the simulated collector tilt angles was the latitude of Rome, which is 41° 51’N. Therefore the first tilt angle was chosen to be 42°, all the other angles were simulated in steps of 10° plus or minus. The simulated draw off takes place every evening at 6.00 pm and lasts until the mixed water temperature turns below 45°C.

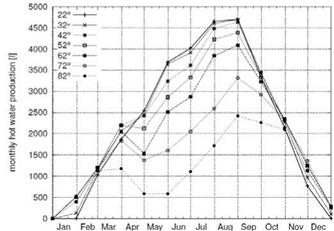Table 2. Determination of the best collector tilt angle in terms of hot water production

Table 2 shows the simulation results in terms of monthly hot water production. It can be seen that the thermosiphon system is able to produce almost the same amount of hot water in the range from 22°.. .52°. Lower system angles, e. g. 22°, should be preferred if hot water is only needed between spring and autumn, e. g. for campsites. If hot water is needed throughout the whole year, a collector tilt angle comparable to the latitude should be preferred, in case of Rome 42°. With collector tilt angles of 62° and more it is not really possible to increase hot water production during winter times as is known from pumped solar hot water systems.

To test the energy management unit of chapter 4, the behaviour of the overall system has to be simulated dynamically. For this task, the software package Matlab/Simulink with the Carnot-Blockset Toolbox has been used and will be presented at the poster at the EuroSun2008.

3. Conclusions and Outlook

The presented project is supported financially by the Austrian “Klima — und Energiefonds in der Programmlinie ‘Energie der Zunkft’”, project partners are Elektrizitatswerke Wels AG, Wels Strom GmbH, ASiC — Austria Solar Innovation Center, University of Linz and BlueSky Wetteranalysen.

References

[1] G. Steinmaurer, H. Dehner, R. Mittasch: Solarthermische Fernwarmeunterstutzung Wels: Rahmenbedingungen, hydraulische Einbindung und Lastmanagement“, ‘Gleisdorf Solar 2008’, 3.-5.9 2008.

[2] : G. Steinmaurer, H. Dehner, R. Mittasch: "Entwicklung des Lastmanagements fur eine solarthermische Fernwarmeunterstutzung am Beispiel Wels", 18. Symposium Thermische Solarenergie, Bad Staffelstein, 23. — 25. April 2008.

[3] G. Steinmaurer, „Optimale Steuerung von Leistungsquellen mit Zwischenspeicher“, VDI-Verlag, ISBN-Nr.: 978-3-18-513008-3