1.1. Atmospheric gases

Firstly, one calculates Ig0 which is the SSI for a clear atmosphere containing none of the six gases nor aerosol. Attenuation in this case is due to the rest of molecules in the atmosphere, which is called background Mbg. Secondly, one computes the clearness index KT0 which is the ratio of Ig0 to the extraterrestrial irradiance I0. Then, one varies the amount of a molecule M in the atmosphere and maintains to zero the other quantities. M will be successively H2O, O3, CO2, O2, CH4, and N2O, thus leading to SSI IgM. The ratio of IgM to I0 gives the clearness index KTM+ for the molecule Mplus Mbg. Since the transmittance of several gases is obtained by multiplying the transmittances of each gas, the clearness index due to the single molecule M is given by:

KTM = KTM+ / KT0

We observe an important variation of the transmittance with molecule and wavelength. Changes in quantities of O2, CO2, CH4, and N2O create a variation of transmittance of the atmospheric column less than 1 / 10000 for all wavelengths. We can thus conclude that changes in these quantities have a negligible effect on radiation. The transmittance of O3 is almost zero for wavelengths less than 0.3 pm. Its change is large in the region [0.31 pm, 0.33 pm] (more than 0.2) and is about 0.02 in the region [0.52 pm, 0.68 pm]. Regarding water vapour, the variation of transmittance which change in content is important in the region [0.57 pm, 4 pm] (Fig. 1 left). In addition, the influence of the atmosphere profile on the range of variation is significant ; the errors committed on the SSI if one does not take the right atmospheric profile are shown in Fig. 1 right.

Figure 1. Spectral transmittance of H2O (on left) for different water content (in kg m-2) and relative error due to
atmosphere profile (on right); the reference model is afglus. Calculations for Kato bands.

1.2. Aerosols

For assessing the deviation on the SSI induced by deviation of the properties of aerosols, one computes the SSI of reference Iaref with the aerosol optical thickness at 550 nm Taer 550 set to 0.1, a to 1.5 and the aerosol types to haze 1 and vulcan 1 and season 1. Then these parameters are changed and one computes the absolute deviation of the SSI to the reference case.

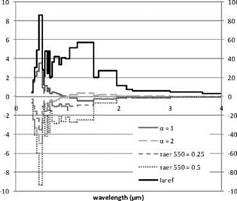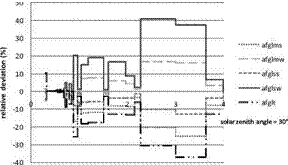
Fig. 2 (left) shows the influence of aerosol optical thickness on the SSI. The deviation due to a is large (up to 20% of deviation on the SSI for a = 2) and decreases as the wavelength increases. As a increases, the SSI decreases. The influence of aerosol optical thickness at 550 nm is similar. Then, aerosol type is changed from haze 1 to haze 4, haze 5 and haze 6, vulcan 1 to vulcan 2, vulcan 3 and vulcan 4 and season 1 to season 2. The influences of the models vulcan and season are very low: the absolute deviations on the SSI are below 0.5%. Fig. 2 (right) shows the influence of the aerosol types on the SSI. The deviation due to model haze (on right) is less important than that due to the aerosol optical thickness and reaches 3 %.

Figure 2. Absolute deviation on spectral irradiance in comparison to the reference case. Solar zenith angle
(30°), water content (15 kg m-2), ozone amount (300 DU) and ground albedo (0). haze 1, 4, 5 and 6 respectively
means rural, marine, urban and tropospheric aerosol type from 0 km to 2 km altitude.

1.3. Cloud

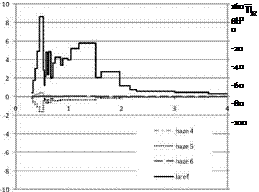
We compute the spectral transmittance of clouds in the same way than the gas transmittances (Fig. 3). An increase in tc leads to a large decrease in cloud transmittance and consequently in the SSI. This decrease is wavelength-dependent. For tc greater than 15, cloud transmittance is very small or null for wavelengths greater than 2 pm. For the same tc, attenuation of radiation is stronger for water cloud than for ice cloud. The decrease in direct SSI is more marked than that in diffuse SSI; the direct SSI normal to sun rays reaches zero for tc around 7.

1st International Congress on Heating, Cooling, and Buildings — 7th to 10th October, Lisbon — Portugal /

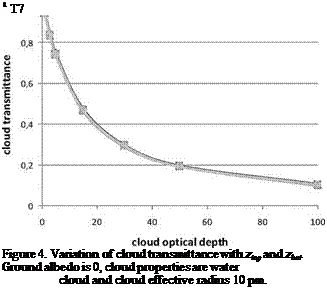
Figure 3. Change in spectral transmittance of clouds with tc. Water cloud, ztop = 5 km, zbot = 2 km, ref = 10 pm.

To assess the influence of ztop and zbot on the SSI, we use the typical values given by Liou (1976) for different types of clouds. Fig. 4 shows the variation of cloud transmittance with ztop and zbot as the function of tc. All curves are superimposed: the maximum difference in transmittance is equal to 0.01 for albedo 0. The influence of ztop and zbot on the SSI is negligible; this is true for other albedos. Similar results are obtained with the ice cloud. Our results are similar to those of Kuhleman and Betcke (1995).

zbot=0, ztop=1 zbot=2, ztop=3 zbot=3, ztop=8 zbot=4, ztop=7 zbot=1, ztop=4 zbot=2, ztop=6 zbot=1, ztop=7 zbot=2, ztop=10

L. Martin1*, L. F. Zarzalejo1, J. Polo1, A. Navarro1, R. Marchante2

1 CIEMAT, Department of Energy, Av. Complutense n°22, Madrid, 28040, Spain

2 IrSOLaV, Calle Santiago Grisolia (PTM) 2, Tres Cantos, 28045, Madrid, Spain

Corresponding Author, luis. martin@ciemat. es

Abstract

Solar energy is gaining huge relevance due to non sustainable current energetic model based on fossil fuels. In the case of solar technology to produce electricity, the integration of power generated into electric grid presents new horizons, such as the estimation of short-range electricity generation to optimize its management; avoiding situations of load reduction and anticipating supplying problems. In this work, a methodology to predict values of solar energy is proposed based on half daily differences of solar radiation lost component time series and qualitative predictions of sky conditions. The dataset used belongs to the radiometric station of Spanish National Weather Service (AEMet) sited in Madrid. Prediction methodology used is artificial neural networks. Skill score of models fed with qualitative prediction as input and without is compared with persistence.

Keywords: Energy meteorology, solar radiation, solar radiation forecasting, solar radiation time series properties, artificial neural network

1. Introduction

Although considerable effort has been done to make use of solar energy efficiently from industrial revolution, expecting fossil fuels would run out in the future, only minimal resources have been directed towards forecasting incoming energy at ground level [1]. However, the necessity to have forecasting models which could optimize the integration of solar thermal power and photovoltaic into electric grid within different sources of electric power generation will grow up as they gain recognition as an energetic resource in the near future.

Photovoltaic and solar thermoelectric power are main sources of solar energy for electricity generation. Currently the potential market is huge and its development is being supported by agreements in Kyoto protocol and by progressive series of regulations regarding green energy (feed-in tariff) established in several countries like Spain and Germany [2]. In the case of Spain, current legislation (Royal Decree 436/2004, 12th of March) allows to minimize investment risks to promoters and to contribute opening up great perspectives to solar energy development.

Energy stock market participation is regulated by two basic rules: on the one hand it is necessary to predict the amount of energy which will be produced, up to 72 hours before, and on the other hand deviations of energy produced compared to programmed one are strongly penalized.

In this work a methodology to predict half daily values of solar energy is proposed, with temporal horizon up to 72 hours. Artificial neural networks techniques are used to predict global solar irradiance values. The prediction is done directly over the differences on solar irradiance measured consecutively. This transformation is done to have a stationary variable with a probability distribution similar to Gaussian distribution.

Forecasting half day values is a first step to make hourly predictions, which is the resolution demanded by legislation. Besides half daily values are of great importance for the operation and energy production programming of concentrating solar thermal power plants which has an storage system.

M. G. Kratzenberg[1]*, S. Colle1, H. G. Beyer2

1 Department of Mechanical Engineering, Laboratory of Energy Conversion Process Engineering and
Energy Technology, Federal University of Santa Catarina, Brazil, Florianopolis, Brazil
2 Institute of Electrical Engineering, University of Applied Sciences Magdeburg-Stendal, Germany

* Corresponding Author, manfred@labsolar. ufsc. br
Abstract

Electric shower heads are widely used in Brazil to provide hot water for domestic use. The total power peak demand due to the shower heads in the period of time between 6:00 p. m. to 8:00 p. m. is around 3.5 GW. The current use of solar domestic hot water systems has proven to be not an effective solution to eliminate this peak power. Therefore, a new concept of intelligent solar systems, which able to operate integrated to the weather forecast information system, should be developed. Storage preheating then could be controlled based on solar energy forecast algorithms. Nowadays the Numeric Weather Prediction (NWP) models have very low forecast performance for the solar radiation. With the intent to increase the performance of these models, its output variables are corrected with Model Output Statistic (MOS) techniques. Therefore NWP model residuals, the forecasted weather variable subtracted from the measured variable are estimated. Even the corrected solar radiation forecasts do presently not have satisfactory forecast performance. In the present work a novel high performance MOS technique is presented which is based on the Discrete Wavelet Transformation (DWT) and Artificial Neural Networks (ANN). The daily solar energy forecast by the presented method reduces the RMSE from 25.5 % to 9.06 % for the site Florianopolis, localized in the subtropical south of Brazil.

Keywords: Numeric Weather Prediction, Model Output Statistic, Discrete Wavelet Transform, Compact Solar Domestic Hot Water Systems

storage only at the early hours of the day during which the electric energy has the minimal effective cost. Under clear sky conditions a reasonable sized CSDHWS should provide satisfactorily the energy that is consumed, and consequently it avoids the demand on electric energy for heating [5]. Under weather conditions other then of clear sky, an additional heating of the water storage is needed. Therefore, forecasting of the total solar energy incident on the tilted collector, EtNWP, as well as the ambient temperature are necessary, in order to identify the gap between the expected solar energy gain and the solar energy gain with this system on clear days. The conversion of the forecasted horizontal solar radiation in its correlated tilted radiation EtNWP can be found in e. g. [6]. The main goal of this paper is to present first numerical results of the forecasted daily solar energy obtained by a novel statistic correction of a NWP model based on the DWT.

D. Pozo-Vazquez1*, V Lara-Fanego1, H. Al-Samamra1, J. A. Ruiz-Arias1, A. Molina2 and J.

Tovar-Pescador1

1 MATRAS Group, Department of Physics,

2 Department of Computer Sciences
University of Jaen, Campus Lagunillas, 23071, Jaen, Spain
* Corresponding Author, dpozo@ujaen. es

Abstract

The solar radiation plays a major role in the energy exchange process between the atmosphere and the earth surface and is, therefore, a key parameter in a wide range of studies related to agriculture, hydrology, ecosystem modelling or renewable energy. It is known that complex topography significantly modifies radiation fluxes at the earth’s surface. Nevertheless, terrain effects on radiation fluxes induced by aspect, slope, sky view factor and shadowing are normally neglected in numerical models when horizontal resolution is lower than 10 km. As spatial resolutions of mesoscales models increase (1-2 Km) the topographic effect on the solar radiation might be considerable, especially at low solar-height angles. Fine-scale non-hydrostatic numerical models, such as PSU/NCAR MM5, are able to include the effects of the slope and aspect on the solar radiation estimates.

In this work we analyze the reliability of solar radiation estimates provided by the MM5 in complex topography. Particularly, hourly global solar radiation values for clear-sky days were obtained based on several MM5 simulations. The experiment was carried out for an area located within the Sierra-Magina Natural Park (Jaen, Southeastern Spain). This area is characterized by a relatively complex topography, with elevations ranging from 600 to 2100 m. MM5 estimates were tested against field data measured at 11 radiometric station located in an area of 20 km x 20 km inside the Park. The location of these radiometric stations covers a wide range of elevations, aspects and slopes. Four experiment was conducted, one per season, corresponding to three consecutive clear-sky days collected along the year 2006. Two 1 km resolution simulations were carried out for each experiment: one including the MM5 topographic parameterization and one without including these effects. The comparative analysis of the results allows both knowing the effect of topography on MM5 high-resolution solar radiation estimates and how the slope and aspect parameterization of the MM5 deals with this problem. Finally, the results were analyzed on the light of the different topographic characteristics of the 11 stations.

Results showed, firstly that, compared to observations, an important improvement is obtained both for temperature and radiation when including the topographic effects in the MM5 simulations. Additionally, the model tends to underestimate the solar radiation in morning day hours and to overestimate the values in the central day hours. Finally, results showed, that the difference between the estimated and measured solar radiation increases when the topographic complexity increases.

Keywords: Global Solar Radiation, MM5, NWP, Complex Topography, Andalusia.

1. Introduction

The renewable energies have the advantage of a smaller incidence in the environment in comparison with other energy sources; however, their production is conditioned by variations in the weather and in the climate. Therefore, although the renewable sources of energy can liberate us partially from dependence of the fossil fuels, they introduce another complicated dependence: the weather and the climate. In Spain, in the next future a strong increment in the electricity production based on solar resources is expected. This strong increment of the dependence of the renewable energy resources, along with their inherent variability, highlights problems related to the security and management of the supply. The future success of the renewable energy will be associated with an appropriate evaluation of the available resources and a correct forecast of its variability. This keeps not only for homogenous flat terrain, the usual location for thermosolar or great photovoltaic power plant, but also in complex topography areas, where many small PV power plants are located. It is in this context where the detailed knowledge of the available solar energy resources and its variability has a strategic importance.

Along the last decades, numerous methodologies have been proposed to address the problem of mapping the solar radiation. Due to technical and economical constraints both the spatial density and temporal coverage of solar radiation measurement are considerable lower that for the case of other key climate variables, as the temperature or precipitation. Additionally, the solar radiation can show a considerable spatial and temporal variability associated with topographic features. Given these constraints, the methodologies used for solar radiation mapping ranges from to the use of satellite estimates to, more recently, the use of Geographic Information System (GIS)-based solar radiation models and, traditionally, the use of the well known interpolation techniques. The recent developments of Numerical Weather Prediction (NWP) models makes these models a promising tool for solar resources evaluation and forecasting, even for complex topography areas. The main advantage, among other, of these models is that they allows not only to estimates the resources but also to forecast these resources. Nevertheless, the use of NWP models to estimate and forecast the solar radiation is still very limited.

It is known that complex topography significantly modifies radiation fluxes at the earth’s surface. Nevertheless, terrain effects on radiation fluxes induced by aspect, slope, sky view factor and shadowing are normally neglected in NWP when horizontal resolution is lower than 10 km. As spatial resolutions of NWP models increase (1-2 Km) the topographic effect on the solar radiation might be considerable, especially at low solar-height angles. Fine-scale non-hydrostatic numerical models, such as the Fith-Generation Penn State University/National Center for Atmospheric Research (PSU/NCAR) Mesoscale Model (Grell et al., 1994), known as MM5, , are able to include the effects of the slope and aspect on the solar radiation estimates. The MM5, is a non-hydrostatic, vertical sigma-coordinate model designed to simulate mesoscale atmospheric conditions. It allows simulating the climate with spatial resolution up to 1 km. The MM5 allows to optionally take into account the topography effects on the solar radiation at the earth surface. Particularly, the models includes parameterization that takes into account the effect of the slope, aspect and shadow cast caused by the topography on the solar radiation.

In this work we analyze the reliability of solar radiation estimates provided by the MM5 in complex topography areas and evaluate the importance of these topographic parameterization of the MM5. Particularly, hourly global solar radiation MM5 estimates values for clear-sky days were obtained using and no using the topographic parameterization of the MM5 model. The study was carried out for region of Sierra Magina (Jaen), a Natural Park characterized by a relatively complex topography. Results were evaluated using a set radiometric stations located in this Park.

2. Experiment design

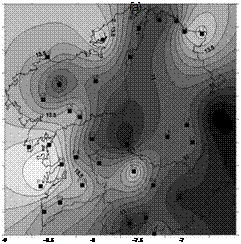Fig. 2 shows the annual mean values of global irradiation recorded during 2006 and 2007. The zones with the highest values of irradiation (greater than 14 MJ m-2 day-1) are located along the south-western border of the Ourense province. This zone is characterized by low precipitations and relative humidity (Fig. 3); however, lowest average annual temperatures (Fig. 4a) compared to the rest of the region are due to the lowest cold temperatures in wintertime, that are not balanced by its highest hot temperatures in summertime; this is typical from this clearer sky zone than the rest of the region.

Fig. 4: Annual mean values of (a) temperature (°С) and (b) daily sunshine hours (hr) over the region.

On the other side, the lowest values of irradiation (less than 11 MJ m-2 day-1) are found in the northern edge of the region, in the southern edge (around Monte Aloia station) and near the stations of Ourense and Sergude. Typical foggy conditions over valleys close to rivers (Ourense and Sergude stations) or along coastal line (northern edge) reduce the sunshine hours, as it is shown on Fig. 4b), so irradiation is lower than in the rest of the region. At Monte Aloia mountain, high precipitation values are achieved (Fig. 3a), due to typical wintertime wet air masses from the Atlantic Ocean carrying rain clouds over this coastal mountain (Foehn effect) [16].

2.1 Clearness Index

Annual clearness index, KT, was estimated in order to evaluate both the influence of local conditions and geographical coordinates over the solar irradiation. As it is observed on Fig. 5 compared to Fig. 2, KT distribution is quite similar to global irradiation map, with extreme values located at the same zones. Therefore, local conditions are the most important affecting the solar radiation that achieved the ground level.

Fig. 5: Annual mean values of clearness index (Xt) over the region.

This comparison shows that either high resolution solar irradiation maps or long term solar irradiation measurements are required to evaluate the solar resource in any location of this region.

G. Lopez1*, F. J. Batlles2 and J. L. Bosch2

1 Departamento de Ingenieria Electrica y Termica, Escuela Politecnica Superior, Universidad de Huelva,

21819, Huelva, Spain

2 Departamento de Fisica Aplicada, Universidad de Almeria, Almeria, Spain
Corresponding Author, gabriel. lopez@die. uhu. es

Abstract

In this work we analyse a daily global irradiance time series into the framework of chaotic dynamic systems in order to examine a possible underlying nonlinear behaviour. Employed methods are based on a phase space reconstruction from the measured data and are devoted to the calculation of the properties of an underlying attractor, such as the Lyapunov exponents. Researches on these dynamical system invariants will point out the presence of chaos. We also use local lineal models as a test for nonlinearity.

The global solar radiation data were measured at the radiometric station of the University of Almeria (Spain) during eight years. Results have shown the non-existence of any attractor in the phase space for the global irradiance time series. Negative Lyapunov exponents exclude a chaotic behaviour that might allow a better short term prediction than autoregressive models, and the idea of the existence of a nonlinear differential equation system. These results match with those obtained from applying local linear models for prediction, of which estimations suggest that the data are best described by a linear stochastic process.

Keywords: solar radiation, forecasting, chaos, nonlinear time series.

1. Introduction

Information on the availability of solar radiation is needed in many applications dealing with the exploitation of solar energy. Particularly, global solar radiation is one of the most important input parameters for any solar energy system and different techniques have been developed to model and forecast it. Once the solar energy system (like concentrated solar power plants) is running, prediction of power load, normally done on an hourly basis with a prediction horizon between 1 and 24 hours, is instrumental for planning and operation of the total power system, e. g. for buying or selling power or for solving the unit commitment and dispatch problems.

Studies about solar radiation time series and other meteorological variables with autoregressive or stochastic models [1-3] have experienced an important growth in the last years, since synthetic sequences statistically indistinguishable from the original ones are needed to design the solar devices properly. However, using this type of model, prediction from past values is limited due to the random character exhibited by these time series. The main factor of randomness affecting global solar radiation data is due to variations in the sky cloud cover, which make the radiation on cloudy days difficult to predict.

Appearing of several nonlinear dynamical models developed by Lorenz [4], with a fully irregular and complex behaviour (generically named chaos), allows to study the nature of fluctuations in solar radiation data from a new methodology. Time series from many system evolutions, apparently evolving in a random way, can now be predicted with higher precision than with traditional ARMA models, at least for short term predictions. Detection of chaos in a time series would thus allow a better modelling of time series against statistically based models.

In this paper, we analyse a daily global solar irradiance time series into the framework of chaotic dynamic systems in order to examine a possible underlying nonlinear behaviour. Existence of chaos should help to improve the short term predictions performed by means of the traditional
statistical techniques. Employed methods are based on a phase space reconstruction from the measured data and are devoted to the calculation of the properties of an underlying attractor, such as the Lyapunov exponents. We also use local lineal models as a test for nonlinearity.

2. Experimental Data

The horizontal global solar radiation time series (symbolized by {xt}, being t the time step in days) consisted of 2945 daily values. They were obtained by integration from experimental values averaged every ten minutes during the years 1990-1992 and every five minutes during the years 1993-1998. The measurements were recorded at the radiometric station of the University of Almeria (36.8° N, 2.44° W) in south-eastern Spain by means of a Kipp and Zonen CM-11 pyranometer. Measurements from other two pyranometers (LI-COR, model LI-200) were also available. They were used to detect and replace any anomalous value measured by the CM-11 pyranometer. The calibration constants of the pyranometers were checked periodically by our research group. Measurements by the LI-200 pyranometers were also corrected following [5].

3. Methodology and results

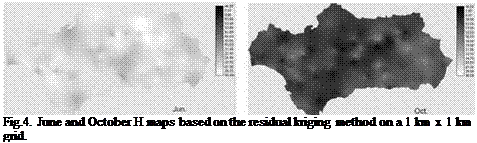Again, as for the ordinary kriging, a seasonal pattern is present, with the summer months showing the lowest RMSE values and the winter months the highest ones. Particularly, lowest RMSE relative value are found for February 0.54 MJ m-2day-1 (4.5%) and the highest for October 1.31 MJ m-2day-1 (10.2 %). MAE ranges from 0.22 MJ m-2day-1 (2.2%) in January to 0.70 MJ m-2day-1 (5.4%) in October. Regarding the ME, the model tends to slightly overestimate the solar radiation, for all the months, but ME values are fairly low. Figure 4 shows the estimated H maps based on the residual kriging procedure.

The clear sky index is an appropriate and thus an established quantity for the description of the transmission properties of the Earth’s atmosphere.

It is defined by

k* = Ig / Idear (3)

where the current global radiation Ig is related to the expected clear sky radiation Idear. In addition a model is needed, which describes the atmospheric conditions, a so called clear sky model, see sec. 2.2.

[Beyer et al. 96] introduced the relation

k* = 1 — n (4)

into the Heliosat method. This relation can be used without a previous calibration with ground data, but it is necessary that the clear sky model is optimally adapted to the regarded area. By Fontoynont et al. [2] relation (4) was improved in order to detail the case of complete cloudiness and to limit the clear sky index to meaningful values.

The influence of the albedo on the SSI varies with the solar zenith angle and the atmospheric turbidity. This influence is assessed by computing the difference between the SSIs obtained with the ground albedo equal to respectively 0 and 0.2 (Fig. 5).

The influence of the albedo on the SSI decreases as the wavelength increase because the intensity of diffusion decreases. It increases with increasing atmospheric turbidity and so, decreases also with increasing visibility. This influence decreases when the solar zenith angle is growing because of the decreasing of the SSI; this is also true for the relative deviation. Presence of clouds increases the relative influence of the albedo: the larger tc, the larger the relative deviation.

The dataset used in this study is based on pyranometric global solar irradiance ground measurements which belongs to stations of the Spanish National Radiometric Network from Agencia Espanola de Meteorologia (AEMet) sited in Madrid (40.45°N, 3.72°W, 680 m.). The period of data acquired goes from 1st of January 1979 up to 31st of December 2003 having 17376 of half daily values.

The quality of pyranometric available data and temporal acquisition of measurements are two crucial factors related to adjustment of proposed models. In this study an exhaustive quality analysis has been done on both important factors which influence high quality measurements (based on BSRN recommendations). Manufacturer of pyranometers used is the Dutch firm Kipp&Zonen and belong to CM11 series.

2. Methodology

The mean daily solar radiation presents a seasonal variation due principally to the variation of the position of the earth to the sun and a stochastic aspect introduced by atmospheric components (aerosols, H2O, O3,…).

Half daily ground solar radiation shows a seasonal trend with fluctuations from day to day due to cloudiness, changing air mass and aerosols. The seasonal trend can be separated in several different ways: (1) “clearness sky index” based on extracting the influence of latitude, dividing between measured ground solar radiation and extraterrestrial solar radiation values, (2) subtraction of the annual harmonic (first harmonic of Fourier analysis), (3) “lost component” which is based on the subtraction of each value of the extraterrestrial radiation the corresponding value of ground solar radiation. In general, approach (1) leads to a procedure much simpler from the point of view of the user, but it is not suitable because statistical forecasting methods needs predictors with stationary behaviour and Gaussian distribution.