Chen zhi-jun has quoted four statistical methods [5] to explain the data characteristic which are based on the monthly data of single station or based on the whole year data of single station or based on the monthly data of all stations or based on the whole year data of all stations. And the results show that the correlation of clearness index and sunshine percentage is to some extent spatial-dependence and time-dependence. And he also proves that the statistical method based on the monthly data of all stations is the best.

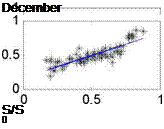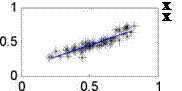
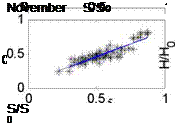
Followings are the figures of statistic result.

Fig. 1. The correlation of H / H о and S / S0 based on the monthly data of all stations in China

2.1. Comparative results

We can obtain the regression coefficient a and b (which are included in our model in the table 2) from the above Fig.1. To determine the predictive efficient of the model developed in this paper, it is pertinent to compare this model with those believed to be universally applicable (Eq10, 11, 12).And the result of these comparisons will determine the applicability of those models to China, as presented in Table 2.

2.2. Discussions

The errors of each model used in the estimation of global solar radiation are tested by calculating the mean bias errors (MBE), the root mean square errors (RMSE) and the mean absolute bias errors (MABE) from Equation (13), (14) and (15). The RMSE shows the discrete degree of the error, and the MABE shows the average status of the relative error, and MBE values obtained from the models are positive in some cases and negative in others, that means a positive MBE means over estimation and a negative MBE means under estimation. And it is observed that the lower the RMSE, the more the accuracy.

As can be seen in Table 2, our model has the best accuracy because the value of RMSE doesn’t exceed 6% which is the minimum in the four models, hence the estimation values of the global radiation can really reflect the real values. The performance of Page model (not exceed 7%)

is slighter better than that of Rietveld and Ogelman et al (they are 7% and 7.14%), the difference of accuracy is very little. With respect to MBE, the positive values of from the models (Rietveld, Ogelman et al, Page) indicate an over estimation, while the Ogelman et al’s model gives the worst over estimation, and our model only has very little under estimation. With respect to MABE, our model also has the minimum of these models and Ogelman et al’s model has the maximum.

By comparison, it is realized that the performance of the Ogelman et al’s model is the worst, and the performances of Rietveld’ (equationlO) and Page’ (equation 12) models are slight poor than that of the model developed in this paper.

The transmissivity of the atmosphere for the global radiation under perfectly clear sky conditions is given as the sum of the regression coefficients, a+b[10] in the figure.2. We can see that the value of the sum gradually becomes small until the July, after that it gradually rises until the November. We know that the probability of raining gradually increases in the first half of the year nearly in most areas of China, lots of clouds after raining often exist in the sky. So the transmissivity is lower than that in the second half of the year because the weather condition will become dry and there are few clouds in the sky. Hence, the result is quite consistent with the change trend of the climate. The average values of a and b are 0.1387 and 0.6367. It is observed that the sum (0.7754) of the values for the coefficient compares well with the value (0.80) reported in literature for the mesothermal forest climate (often dry season in winner) [9]. Because most areas of China are located in the mesothermal forest climate.

From the above comparisons, everything points to the fact that Angstrom-Prescott-one parameter-model is, to a large extent, locality dependent (It is expected that the performance of any general equation will always be poor than that of the model developed for that locality.)

3. Conclusion

The present work of this paper is that a linear correlation form of Angstrom-Prescott correlations has been developed for use in estimation global radiation of China. And the model is also compared with other models (Rietveld, Ogelman et al Page) in terms of different parameters. Comparative analysis shows that the predictive accuracy of our model is far better than the rest of

the models considered in this study. Hence the monthly average daily global radiation incident on the horizontal surfaces can be estimated by the correlation developed in this paper (the error doesn’t exceed 6%). Especially for the places where there are no stations for measurements but have similar meteorological conditions in China.

4. Acknowledgment

The author is grateful to the CMA (China Meteorological Administration) for providing the data.

References

[1] T. Muneer, Solar Radiation and Daylight Models for the Energy Efficient Design of Building(Architectural

Press, Oxford,1997)

[2] S. U.UDO, Contribution to the Relationship between Solar Radiation and Sunshine duration in the Tropics:

A Case Study of Experimental Data at Ilorin, Nigeria. Turk J Phys 26(2002)

[3] JIANG Ying-ni, Models for estimating monthly mean daily Diffuse Radiation. [J]

[4] Louis E. AKPABIO, Modeling Global Solar Radiation for a tropical location: onne, Nigeria

Turk J Phys 29(2005)

[5] Chen Zhi-jun, Exporing the monthly clearness index models in china, 2005.10, Journal of Nanjing Instutude of Meteorology

[6] Louis E. AKPABIO, Relationship Between Global Solar Radiation And Sunshine Duration for Onne, Nigeria, [J] Turk J Phys 27(2003)

[7] Zhou Jin, Sunshine-based model for estimation global solar radiation in China, [J], Journal of harbin

institute of technology

[8] Lin Wenxian, Ranking the overall performance of eight sunshine-based global solar radiation models

with a nonparametric statistical procedure,[J] New Energy, 1998. 20(2). 16-19

[9] William A. Beckman, Solar engineering of thermal processes, second edition 39-40, 70-71

[10] K. J.A. Revfeim, An interpretation of the coefficients of the Angstrom equation. Solar Energy. 31,

(1983), 415

For each of the four {ss} time series a specific ANN is trained with an improved Back Propagation (BP) algorithm [9]. In the present work an ANN with a simple optional feedback connection was used (Figure 2, left line).The feedback line transforms the used Feed Forward (FF) ANN in a Recurrent Neural Network (RNN). The blank rectangles in figure 2 symbolize the activation functions, those one with z-1 a one day delay, and those one with the unity represent the unity inputs for the bias weight connections. Each layer of the ANN includes dendrite connections with its weights, designed by sloped lines. The dendrite summation point of the neurons is designed by circles and the output activation functions by blank rectangles. A bipolar sigmoidal activation function for the neurons in the hidden layers and a bipolar linear activation function for the output neuron were applied. The input and output signal were normalized to appear in the range (-1…1) utilizing the normalization equations in [9]. By a conventional BP algorithms, the weights [wu] at iteration step u are updated as a function of the matrix [n {5u} {yuT } ] of eqn. (4). Whereby {5u} is the propagated error at the output of an arbitrary layer of the ANN, n is the pre-adjustable learning rate and {yu} is the output of the previous layer.

[ w u+i ] = [ Wu ] + nx [ {5u} (VuT } ] + a [ w u — w u-i ] (4)

As the present ANN has only one neuron in the output layer, {5u} is a variable (5u) and the weights matrixes in eqn. 4 are all vectors. In order to improve the convergence speed online training, rather than batch training is used, where the ANN weights are updated for each daily mean [30].

By the BP the error energy E (eqn. 3) is propagated back due to partial differentiations, hence sAsi = sAsu = 5u is obtained at the ANN output layer [30] (Figure 2). If during the training 5u = f(u) a local minimum of 5u is separated from the general minimum by high walls, with high A5u = f (Au) gradients, the algorithm may need too many steps to climb the walls moving out of the local

minimum and it runs the risk of being trapped [30]. Therefore were used as learning rates px, two distinct pre-adjustable values, one p(-A5u) = 0.008 for decreasing 5u residuals and another p(A5u) = 0.013 for increasing 5u. The former is used to minimize the uncertainties by learning and the latter enables the algorithm to climb the walls more quickly by increasing residuals in order to search the global minimum. An adjustable momentum factor a = 0.8, increases additionally the weight actualization (eqn. 4) and thus the learning speed, at locations where the learning process occurs with more success. These locations are identified by the weight modification gradient, of the last two learning steps [wt — wt-1]. For higher gradients the matrix a [w t — w t-1] accomplish higher weight modifications and vice versa. The decrease of the weight actualization avoids that the algorithm jumps over a narrow global minimum and therefore increases the stability of the learning process [30].

A multiple regression analysis was carried out independently for each month using the elevation and the semi-sky-view factor as independent explanatory variables. A step-wise procedure was used for the regression parameter estimation. Particularly, the semi-sky-view factor was firstly regressed as independent variable and then the elevation was added. A t-test was carried for each step of the regression procedure and only parameters statistically significant at 5% level were further considered.

The most important explanatory variable is the semi-sky-view factor, which is statistically significant for all the months. This explanatory variable is able to explain from a minimum of 13% of the spatial variability (February) to a maximum of 45% in June. On the other hand, the elevation showed to be statically significant just from March to August and associated explained variance is considerable lower than for the semi-sky-view factor: values ranges from a minimum of 9.7% in August to a maximum of 15% in June. When considering both explanatory variables, explained variance ranges from a minimum of 13.2% in February to a maximum value of 46.7% in June, with most part related to the semi-sky-view factor, which is negatively correlated to the monthly solar radiation data.

The satellite measures the sunlight in the visible spectral region reflected by the earth. Hence the measurement signal depends on the irradiation hitting the reflecting layers. After subtraction of the radiometer offset Co the remaining Count behaves proportionally to the irradiance I. Under utilization of these proportionalities the relative reflectivity p can be defined as standardized backscattering value:

p := C-Co /1. (1)

In the following only relative differences not absolute values of the reflecting properties are important therefore it is sufficient to divide by the cosine of the sun zenith.

1.1.1 Cloud Index

The standardized backscattering values of clouds usually exceed those of the Earth’s surface, excluding the case of snow. Thus it is possible to identify the occurrence of clouds. If the reflectivity for a completely cloudy pixel pc and the reflectivity of the unclouded ground (and ocean respectively) pg is known, the cloud index n as a degree of cloudiness can be defined as

n = (P — Pg)/(Pc — Pg). (2)

If the maximum and minimum of the standardized backscattering values of a pixel is selected as reference values, the Cloud index takes values in the range of 0<=n<=1.

Armel Oumbe1*, Lucien Wald1, Philippe Blanc1, Marion Schroedter-Homscheidt2

1Ecole des Mines de Paris, BP 207, 06904 Sophia Antipolis, France
2German Aerospace Center — German Remote Sensing Data Center, Postfach 1116, D-82234 Wessling, Germany

Corresponding Author, armel. oumbe@ensmp. fr

Abstract

Solar radiation is modified in its way downwards by the content of the atmosphere. Quantifying the influences of the parameters describing the optical state of the atmosphere is necessary for development of a method for the assessment of the solar surface irradiance (SSI). This paper performs an inventory of the variables (e. g., cloud) and their attributes (e. g., optical depth) available in an operational mode and then assesses to which degree the uncertainty on an attribute of a variable -including the absence of value — leads to a departure from the perfect result, i. e., when assuming that all attributes are known with a perfect accuracy. Clouds are the most important variable for the SSI. Aerosol loading and type, water vapour amount and atmospheric profile have a great influence. Ground albedo has an important influence on diffuse part and spectral distribution of SSI. The influences of vertical position and geometrical thickness of clouds in the atmosphere are negligible. Thus, the solution of the RTM for a cloudy atmosphere is equivalent to the product of the irradiance obtained under a clear sky and the extinction coefficient due to the cloud. The results are combined with the data availability for design of the new method Heliosat-4 for assessing the SSI.

Keywords: solar radiation, atmospheric optics, satellite images, Heliosat method

1. Introduction

A wealth of methods has been developed in the past years to assess solar surface irradiance (SSI) from images taken by satellites (Cano et al. 1986; Pinker et al. 1995; Hammer 2000; Rigollier et al. 2004). Current methods are inverse, i. e., the inputs are satellite images whose digital counts result from the ensemble of interactions of radiation with the atmosphere and the ground and the method deduces the radiation from the inputs. On the opposite, solar radiation may be assessed by a direct method, i. e., the various processes occurring during the path of the light from the outer space towards the ground can be modelled by the means of a radiative transfer model (RTM) in 2D or 3D. RTMs take into account a large number of inputs: optical properties including spectral aspects of gases, aerosols, clouds and ground reflectance, types of interactions, mathematical solving methods (Kato et al. 1999; Liou 1976, 1980; Mayer, Kylling 2005; Perrin de Brichambaut, Vauge 1982; Vermote et al. 1997). The quality of the results depend strongly on the quality of the inputs.

Nowadays, the exploitation of recent sensors and satellite data such as MSG, Envisat and MetOp combined with recent data assimilation techniques into atmospheric modelling offers a favourable context for the design and exploitation of a method based on direct modelling. Despite noticeable

advances in the operational assessment of optical properties of the atmosphere at any location, we do not have enough information for 3D RTM. The available atmospheric information is typically 2D.

Even so, many of the inputs are unknown. Some are known every % h (clouds), others every day (ozone, water vapour) and others only from times to times (aerosols). The ground albedo and its spectral distribution is known only if the sky is clear. Furthermore, if available, these quantities are known at different spatial resolutions. Hence, the set of inputs to the RTM is heterogeneous with respect to spatial coverage, spatial sampling step, spatial support of information, temporal sampling frequency, temporal support of information, and accuracy.

The goal of the work presented here is to perform an inventory of the variables (e. g., cloud) and their attributes (e. g., optical depth) available in an operational mode and then to assess to which degree the uncertainty on an attribute of a variable — including the absence of value — leads to a departure from the perfect result, i. e., when assuming that all attributes are known with a perfect accuracy.

The spectral region of interest is [0.3 pm, 4 pm]. Energy-related applications require spectrally — integrated or spectrally-resolved SSI. For this sensitivity study, we use: the code libRadtran (Mayer, Kylling 2005) because it is accurate, versatile and well exploited in atmospheric optics (Bernhard et al. 2002 ; Mueller et al. 2004 ; Ineichen, 2006); the correlated-k approach of Kato et al. (1999) for spectral resolution; the radiative transfer solver DISORT (Stamnes et al. 1988).

User guidance is one of the main objectives of the MESoR project. This will be realized by the development of a guide of best practices in the application of solar resource data. The above described benchmarking will be one chapter in this guide. The results will give the users a better indication of the uncertainty of the available data sources and which data bases are suitable for different applications. Best practices in the application of solar resource information will be demonstrated in use cases. The applications taken into account by the guide will cover photovoltaics, solar thermal, solar concentrating and daylighting systems. As a basis it will cover requirements and examples for the design of these systems. Further it will cover solar forecasting applications.

1.3 Roadmap

Based on the feedback from the stakeholders and the benchmarking results road map documents are foreseen within the MESoR project. They will cover future research objectives in the field of solar resources, new solar radiation services to faster deploy the market for solar energy applications and optimize grid integration and recommendations for an improved Earth Observation system to better support solar energy.

ERA-40 is a reanalysis of the global atmosphere and surface conditions for 45-years, over the period from September 1957 through August 2002 by ECMWF. Many sources of the meteorological observations were used. This data was run through the ECMWF computer model at a 40km resolution. As the ECMWF’s computer model is one of the more highly-regarded in the field of forecasting, many scientists take its reanalysis to have similar merit. The data is stored in GRIB format. The reanalysis was done in an effort to improve the accuracy of historical weather maps and aid in a more detailed analysis of various weather systems through a period that was severely lacking in computerized data. With the data from reanalyses such as this, many of the more modern computerized tools for analyzing

storm systems can be utilized, at least in part, because of this access to a computerized simulation of the atmospheric state.

The period of data studied goes from 1994 to 2004 and the variable studied is downward global solar radiation. The resolution of the dataset is 1° or 100km.

Accuracy of each one of the models presented is studied in terms of Root Mean Squared Deviation (RMSD):

being N the population size, O the variable observed and O* predicted variable.

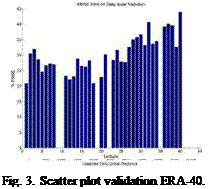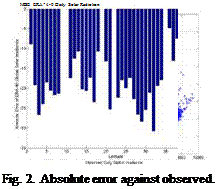
The validation is done comparing with ground measurements from 40 stations from AEMet. Results from validation can be show in Figs. 2-5. . The graphic shows all the stations ordered from lower latitude to higher latitude. Overall data is underestimated for high solar radiation values and Normalized RMSD goes from 20% to 45% and the error gets increased with the latitude.

We have shown in earlier work how a simplified model can be used to achieve a good fit to the global irrad — iance data [2]. The following expression shows that the global irradiance on a horizontal surface IG as the sum of two terms: the first term expresses the direct solar beam irradiance, and the second term expressed the diffuse irradiance due to Rayleigh and Mie scattering from molecules and aerosols in the sky and from clouds.

Ic = U0 F, a1 slnV — I,

I0 = 1367 W/m2 is the solar constant. FJ takes account of the yearly variation of the solar irradiance due to the elliptical orbit of the earth around the sun. A practical equation for FJ is available in reference [6]. The factor aL accounts for the attenuation of direct beam irradiance due to absorption and scattering, where L is the Rayleigh air mass. Finally, the factor sin V takes the geometry of the situation into account for a solar elevation angle V. The solar elevation angle can be computed with knowledge of the latitude, the solar declination angle and the local time. The equation required is widely available in the literature of solar energy design [6].

The air mass L through which the direct rays of the sun must pass depends of course on the angle V between the horizontal and a line from the observer to the center of the sun. For angles V > 250 a simple drawing will show that the air mass L = 1/sin V, for in this case it is reasonable to assume that the earth is a flat surface with a thin layer of atmosphere. However, for angles less than 250 with the sun low on the horizon it is essential to take the curvature of the earth and temperature gradients into account. Fritz Kasten and Andrew

Alberto Pettazzi, Jose Antonio Souto Gonzalez*

Department of Chemical Engineering, University of Santiago de Compostela, Lope Gomez de Marzoa St.,

Campus Sur. 15782 Santiago de Compostela, Spain
Corresponding author, ja. souto@usc. es

Abstract

A basic target of the Renewable Energies and Energetic Sustainability MSc Degree organized by the University of Santiago de Compostela is to provide to the students an adequate knowledge about the estimation of solar resource. Students of this MSc in 2007-08 academic year were involved in analysing and processing solar radiation measurements provided by the Galician weather stations network (www. meteogalicia. es). By the combination of their results, a solar resource map may be obtained and, in addition, it will be compared to other solar resource estimations at Galicia.

Apart from the good results of this work in terms of self-learning teaching, comparison of solar irradiation distribution to other results obtained processing satellite data shows the necessity to consider local effects in the estimation of the solar resource at this region. Keywords: self-learning, solar resource, ground-satellite comparison

1. Introduction

The development of technologies for renewable energies is a priority target in the policy from different fields. To reach this goal, the education on these issues is of primary importance.

A basic target of the Renewable Energies and Energetic Sustainability MSc Degree organized by the University of Santiago de Compostela is to provide the students an adequate knowledge about the estimation of solar resource.

Several works dealing with solar climatology may be found; solar radiation atlases are obtained by different techniques, as satellite measurements ([1], [2], [3]), ground measurements ([4], [5]) or combining ground data with radiative transfer models [6]. In Galicia (NW Spain), Vazquez et al. [7] elaborated a solar radiation atlas using Meteosat-6 satellite measurements [8] over the years 2002-2004. In this work, atlas data were compared against two pyranometers located in Vigo and A Coruna (see Fig. 1).

Following the methodology used by Pettazzi et al. [9], 34 students of the Solar Radiation subject of the MSc above mentioned during 2007-08 academic year were involved in analysing and processing solar radiation measurements provided by the Galician weather stations network [10], from September 2006 to August 2007. The task committed to the students included annual and seasonal analysis of the following parameters: global irradiation, sunshine hours and clearness index, KT. Additional analysis of other climatologically relevant parameters — temperature, relative humidity and precipitations — was also undertaken.

By the combination of their results, solar resource maps have been obtained and, in addition, were compared to results achieved by Vazquez et al. [7].

The performance of the NWP model ARPS and the proposed MOS procedure is verified for the site Florianopolis, localized in the south of Brazil with 48° 3ri5’’W longitude and 27° 36’ 76’’S latitude. The measured global horizontal radiation within the period from January 2000 to June 2006 was used to calculate the daily mean values. For daily mean values, the utilized pyranometer CM11 has a measurement uncertainty of 1 % for 95 % confidence as stated in [31]. For the quality control [32], [33] the measured radiation vales have to appear in the measurement range of (0 to 1367) W/m2. If this criterion was not fulfilled for a time interval larger than 10 min, the daily mean value was rejected as recommended in [33]. From the training-validation of 6.5 years, 119 days were excluded by the quality criterion, leading to the remaining data, which appears in 53 consistent time series. To facilitate the implementation, the data blocks of the training data set were chained, rather than is accomplished a specific DWT of each block, obtaining three equal length vectors with synchronized day numbers. The vector of residuals {sA} is obtained by subtraction of the measured {H} from the forecasted daily solar radiation means {HA}. The obtained predictors sAsi_1 to sAsi-k and predictands sAsi (eqn. 3), selected from the partially reconstructed sub-signals (eqn. 2, {sAS}), have to consider the limitations of each of the data blocks to avoid uncharacteristic modification of the ANN input pattern. As to see in eqn. 3, the data of the first k days of each block are used exclusively as predictors, thus a time series with the length nj provide (n-k) training samples for the ANN. Each sample has an input vector with the pattern length k, the predictors, and one output variable, the observed predictand, of the forecast at the considered time scale. The total number of training-validation samples ntv is obtained with expression (5).

ntv = YU (nj — k ) (5)

Where j = 1…nb defines the number of data blocks obtained by the data qualification, with block individual number of training samples nj. The resulting data set is subdivided in two subsets, the training and the validation set. As recommended in Kaastra [34], the validation set, which is independent from the training set has to represent (10 … 30) % of the data. This set may be selected randomly from the data or it follows immediately the training set [34]. From the data the last year, representing a validation set of 18 % was separated. Due to hardware improvements of the measurement system [35], the validation set was not exposed to system outages, which leads to its consistence.

4. Results

The average of the selected daily mean values of the measured solar radiation is 182.36 W/m2. For ARPS model simulations, based on the reanalysis dada, was obtained a RMSE of 70 W/m2 that corresponds to 38.4% of the measured average value. The maximal error of the daily mean solar radiation simulation is with 264.3 W/m2 higher than the measured average value (compare figure 3 — third chart and figure 4). If the correction is build up with data of twelve subsequent previous days (k = 12), a set of 1356 predictor vectors (sAs, (i-1) … sAs, (i-k) ) were selected. With the proposed MOS method the RMSE of the ARPS model reduces to 18.92 W/m2 for the training data set, which corresponds to 10.37 % of the measured average value of 182.36 W/m2. For the independent validation data set was obtained 9.06 % (see figure 3, fourth chart and figure 5). Worst performances were observed for the sub-signal di which contains the details of the higher frequency band (RMSE = 9.08 W/m2) and for the approximation sub-signal a1 (RMSE = 6.82 W/m2). The generalization performance of the ANN was verified with the validation data set. By arbitrary configured number of neurons in each layer with (k = 12), the best performance of the d1 sub-signal correction was observed, for 22 neurons at the first, and 12 neurons at the second hidden layer. This configuration of the neurons was used also for the other three ANN, whereby the one used for the approximation signal was configured as RNN, due to slight improvement in its performance. To access the probably higher boundary uncertainties under operation of the prediction model, it is necessary to accomplish ntv times (equation 5) the DWT for the data set having ntv predictor/predictand samples (see discussion in section 3.2). Avoiding numerical effort, the present article release only the results based on a single DWT of the data set as accomplished in

[9] .

Figure 3 — Daily mean values of the solar radiation — charts from the top to the bottom: (1) measured solar radiation H; (2) forecasted solar radiation with the ARPS model HA; (3) (H — HA); (4) (H — HA, corr), where HA, con — is the corrected ARPS forecast. The validation set appears from 2000 to 2500 days.