The maps give good insight into regional differences, however due to the coarse grid resolution (5 arc minutes) they smooth out local effects. Some of the integrated systems incorporate specific algorithms, such as an application of high-resolution Digital Elevation Model (DEM), which may increase the difference between results for a given site. Thus, for a set of 37 randomly selected points we analyse the values and resulting differences that a user obtains for a particular site when consulting directly each data source/system. In areas with higher agreement of all 6 databases (standard deviation lower than 4%) we selected 15 points, and in areas with higher disagreement (standard deviation between 5% and 11%) another 22 points.

For each point we calculated the yearly sum of global irradiation for (1) south-oriented surface inclined at 34 degrees (close to the typical optimum angle for PV systems in Europe), and (2) for 2-axis sun-tracking systems.

3. Results

While the map of yearly sum of global horizontal irradiation (Fig. 1) shows the average of 6 databases, the map of standard deviation (Fig. 2) indicates how much the datasets differ in various regions. Higher disagreement between the databases can be found not only in higher mountains (the Alps, Pyrenees, Carpathians, etc.), but also along some coastal zones and in flat regions, e. g. around the Baltic and North Seas. Higher standard deviation in Bulgaria and Romania, in South Scandinavia, and Po plain relates to uneven distribution of the input ground data and questionable quality of the older ground measurements that are used in ESRA and PVGIS. However, cumulative distribution of the map values (Fig. 4 right) shows that standard deviation does not exceed 6% in 78% of the study region, and only in rare (extreme) cases is it higher than 12%.

The analysis on 37 selected points shows some cases with higher differences (some of them are not present in the coarse-resolution maps) with average standard deviation 5.6%. Mean bias difference (see yellow box in the Fig. 3) indicates that satellite databases (Satel-Light and HelioClim-2) show generally higher values compared to the products relying on ground measurements (ESRA, Meteonorm and PVGIS). This difference may be partially explained by the time period of data covered. While Satel-Light and HelioClim-2 represent last 10 years, ESRA and PVGIS are based on one decade of data (1980s), and Meteonorm represents two decades (1980s and 1990s). The NASA SSE product partially spans both periods and also generally gives results that are intermediate between the two groups.

Part of the contribution from higher values obtained from HelioClim-2 database can be probably explained by Mean Bias Deviation calculated by comparison with data from 11 high-quality BSRN stations ([9] see Tab. 1).

For the same 37 points, global irradiation has been calculated for a south-oriented surface inclined at an angle of 34 degrees. Results from five systems are available (all except HelioClim-2). From linear fit of the values on the scattergram (Fig. 4 left) one can see that the standard deviation of

estimations for an inclined surface increases in average by 21% compared to the horizontal irradiation (correlation coefficient 0.98). The differences between values for 2-axis tracking surface are calculated only for 3 systems: Meteonorm, NASA SSE/RETScreen and PVGIS. Here the standard deviation increases by 36% compared to the estimates for horizontal surface (correlation coefficient 0.97). Both simulations show a good agreement in the implementation of the underlying algorithms in the compared software.

By integration of findings from the map and point analyses (Figs. 2 and 4 left) we can estimate uncertainty for any point on the map for yearly values for horizontal, inclined and 2-axis tracking surfaces. Thus the cumulative distribution of user’s uncertainty can be calculated from the map data for the whole study region. Fig. 4 (right) shows that for 90% of the study region the

uncertainty of estimates of yearly global irradiation (expressed by standard deviation) is lower than 7% for a horizontal surface, 8.3% for a south-facing surface inclined at 34°, and 10% for a 2-axis tracking surface.

4. Discussion

Differences in the estimates using several solar radiation databases relate to a number of factors.

Analysis of interannual variability for 70 meteorological stations over Europe having data for at least 10 years shows that the standard deviation from the long-term average ranges typically between 3% and 6%. To capture this variability, a database should include data for at least 5 to 10 years depending on the climate region.

There is an inherent difference between in situ (ground) and satellite observations, and the methods how these data are processed. Databases relying on the interpolation of ground observations (Meteonorm, ESRA, and PVGIS Europe) are sensitive to the quality of measurements and density of the measuring stations (which is not satisfactory in many regions), and they typically represent only statistical values. The satellite-derived databases (e. g. HelioClim, NASA SSE, and Satellight) are more affected by higher uncertainty of the cloud cover assessment when the ground is covered by snow and ice and for low sun angles, but they offer time series with high time resolution (e. g. hourly data) and provide spatially-continuous coverage.

Quality and the spatial detail of spatial database is determined by input data used in the models, mainly parameters describing the optical state of the atmosphere (such as Linke atmospheric turbidity, ozone, water vapour, aerosol optical depth), and Digital Elevation Models. The community of data developers lacks high quality aerosol data. High-resolution DEM is presently considered only in Meteonorm and PVGIS. Databases with coarser spatial resolution (e. g. NASA SSE) provide good regional estimates, however for studies at local level they may show deviations as they ignore local climate and terrain features.

The cross-comparison approach presented in this study assumes that each database has equal weight. Uncertainty can be reduced by weighting each contribution that is based on indicators of quality, number of data-years included, spatial resolution and incorporation of terrain effects. Including another two European satellite-derived databases, those owned by German Aerospace Center (DLR) and University of Oldenburg (both in Germany), and application of weighting will provide more complete picture of the uncertainty in the solar resource assessment.

5. Conclusion

This study provides a first insight into spatial distribution of uncertainty of solar radiation estimates by relative cross comparison of six data sources. In this stage only the yearly sum of global irradiation is considered, and all databases are assumed to give an equal contribution to the overall average. The map of standard deviation from the average indicates combined effect of differences between the databases, and in this study it is used as an indicator of the user’s uncertainty.

Differences at the regional level indicate that within 90% of the study region the uncertainty of yearly global irradiation estimates expressed by standard deviation does not exceed 7% for horizontal surface, 8.3% for surface inclined at 34°, and 10% for 2-axis tracking surface. A user has to expect higher differences in the outputs from the studied databases in complex climate conditions of mountains, some coastal zones and in areas where solar radiation modelling cannot rely on sufficient density and quality of input data.

References

[1] J. Remund, S. Kunz, C. Schilter, Handbook of METEONORM Version 6.0, Part II: theory. Meteotest, 2007, http://www. meteonorm. com/.

[2] J. Greif, K. Scharmer, Eds., European Solar Radiation Atlas (ESRA), 4th edition. Scientific advisors: R. Dogniaux, and J. Page; Authors: L. Wald, M. Albuisson, G. Czeplak, B. Bourges, R. Aguiar, H. Lund, A. Joukoff, U. Terzenbach, H.-G. Beyer, and E. P. Borisenko, Paris: Presses de l’Ecole des Mines de Paris, 2000.

[3] D. Dumortier, M. Fontoynont, D. Heinemann, A. Hammer, J. A. Olseth, A. Skartveit, P. Ineichen, C. Reise. Satel-Light, a www server which provides high quality daylight and solar radiation data for Western and Central Europe. CIE 24th Session, Warsaw, pp. 277-281, 1999. http://www. satellight. com/core. htm.

[4] Surface meteorology and Solar Energy (SSE) Release 6.0 Methodology, draft version 1.005, 2008, http://eosweb. larc. nasa. gov/sse/. Accessible also through RETScreen software http://www. retscreen. net/.

[5] C. Rigollier, M. Lefevre, L. Wald, The method Heliosat-2 for deriving shortwave solar radiation from satellite images, Solar Energy, 77 (2004) 159-169, http://www. helioclim. org/radiation/. Accessible also through SoDa portal http://www. soda-is. com/.

[6] M. Shri, T. Huld, T. Cebecauer, E. D. Dunlop, Geographic Aspects of Photovoltaics in Europe: Contribution of the PVGIS Web Site. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 1 (2008), in press, http://re. irc. ec. europa. eu/pvgis/.

[7] J. Remund, Quality of Meteonorm Version 6.0. Proceedings of 10th World Renewable Energy Conference, 19-25th July 1008, Glasgow. (2008).

[8] H.-G. Beyer, G. Czeplak, U. Terzenbach, L. Wald, Assessment of the method used to construct clearness index maps for the new European Solar Radiation Atlas (ESRA), Solar Energy, 61 (1997) 389-397.

[9] P. Inneichen, Irradiance products validation and comparison against 13 ground stations, Working document of the MESoR project, 2008, http://www. mesor. net/.

1.1. Research platform

The Danish King Christian VIII sent the first Galathea Expedition to the Far East in 1845-1847. The second Galathea Expedition took place 100 years later from 1950-1952, devoted primarily to ethnographic research. The present paper describes data collected on the Galathea III Expedition which was undertaken from August 2006 through April 2007. Figure 1 shows the Royal Danish Navy (RDN) vessel Vsdderen which was converted to a research platform for the expedition.

2.2 Data collection

Data was integrated over 10-minute intervals and recorded with a Cambridge Scientific CR10X data logger along with date, time and position information. Data was uploaded via a satellite link to the internet weekly. Thanks to excellent support from the Danish Department of Fisheries a complete data set is available for every single day of the 8 month expedition. This high level of data integrity is partly because the data logger was battery powered with a continuous trickle charge and could be independent of external power during for up to several days if necessary. The complete data set has been placed on the internet, and it is available in Excel format at the home page www. soldata. dk. Click on the link “Galathea data…”.

The results of this proposed model are compared with three other previously reported models which are believed to be applicable anywhere in the world and yield superior results for cloudy

conditions.

( і) Rietveld model [2]

Rietveld examined several published values of a and b, and noted that a is related linearly and b hyperbolically to the mean value of S / S0 such that

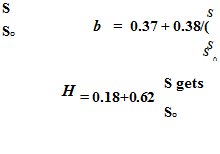
(9)

Substituting a and b in Eq (1), one

(10)

(ii) Ogelman et al model [2, 4]

Ogelman et al proposed the use of a correlation which relates the global solar radiation to S / S0 in a quadratic form as

(11)

(iv) Page model [8]

Page quoted a correlation which was believed to be suitable anywhere.

H c

= 0.23+0.48 H S0

The three models listed above were applied to the sunshine data in China. The calculated and measured values of average daily global radiation on the horizontal surface were compared using the following parameters.

1.2. Comparative parameters

In order to compute the deviation and compare the results of above models, this paper makes use of following parameters.

RMSE
(13)
estimated______ measured H measured
/ N
(14)

N

MBE = [I (Hestimated — Hmeasured )] / N

i=1

RMSE: Root Mean Square Error MABE: Mean Absolute Bias Error

MBE: Mean Bias Error

Hestimated : the estimated value of the global solar radiation Hmeasured: the measured value of the global radiation

He: the arithmetic mean value of the m estimated values of the global solar radiation

Hm : the arithmetic mean value of the m measured values of the global solar radiation N: the number of the data

2. Results and Discussion

The NWP uncertainties of the rainfall forecast is based on non-stationary, nonlinear and dynamic effects as stated by Todini [18]. The solar radiation forecast, also a function of the cloud cover, is expected to be subjected to the same underlying effects. Time series models which using the DWT are capable to interpret non stationary effects as stated in [27] and time series models using the auto-regression (AR) models are capable to interpret dynamic effects [28]. Applying the AR model to the Haar and the bi-orthogonal DWT family, shows that the highest order bi-orthogonal wavelet transform of the Matlab™ tool set (bior6.8) :, has the best performance for the DWT-AR MOS of the solar radiation correction as shown in [29]. Thus, it can be considered, that the DWT, which uses the highest order bi-orthogonal wavelet corrects best the dynamic and non stationary characteristics of statistic MOS model. Improving the correction of the non linear effects, the AR model is substituted by an ANN in the present article.

3.1 Statistical correction of the NWP model output

The idea of the proposed statistical correction method is based on the time series correction MOS as presented in [15] for local correction. The Kalman Filter is substituted by the ANN-DWT (section 3.5). This method is utilized to estimate the correction of the solar radiation for the forecasted day, based on the recognized pattern of the NWP residual obtained from twelve previous days. The residual {sA} between the measured {H} and the forecasted daily mean solar radiation {HA} is estimated to correct the NWP output with this estimations {sA}. The forecasted {HA} and the measured {H} solar radiation time series are in a first step both decomposed in its sub-series {HAs} and {Hs} by the DWT. For mx time scales one obtains s = 1 … (mx + 1) sub­signals of residuals {sas} of the ARPS forecasts by the equation (2). For s = 1 … mx, the vectors {sas} are the sub-signals which represent the details and for s = (mx + 1), the {sas} is the sub­signal which represents the approximation of the ARPS residuals.

{sas} = {Has} — {Hs} (2)

The independent {sAS} sub-signal vectors can also be obtained by the direct decomposition of the residual vector {sA}. Each of these time series is utilized for the training of its corresponding ANN, minimizing the squared error (eqn. 3) in a supervised learning process [30] to estimate the predictand sAs i for the day i, based on the characteristic pattern of the predictors, the sAS — values of (i-1) to (i-k) previous days. The symbol E stands for the energy of the error [30].

E _ 2 ^^i-j (s As, i (sAs, (i-1) ■■■ sAs, (i-k)) — sAs, i) ^ тІП (3)

This function has a support length of thirteen sampled discrete values.

The forecast output of the NWP model is corrected with the sum of the (mx+1) estimated residual values ё а5,і.

In this work, we have only considered explanatory variables that can be derived from DEM. This makes the results more general and useful, since these variables are readily available elsewhere. Particularly, in this study we have evaluated the effect of the elevation and shadows cast as external variables in the kriging procedure. To deal with the seasonality of the solar radiation variability, the study is carried out for each month independently. The topographic characteristics were derived based on a 1 km spatial resolution DEM and the IDRISI GIS software [6] was used to carry out the regression analysis and the whole residual kriging procedure.

Regarding the elevation, it is clear that this variable is related to the atmospheric attenuation of the incoming solar radiation at the earth surface. The higher the elevation, the lower the atmospheric layer thickness and, therefore, the lower the atmospheric attenuation. Nevertheless, the importance of this explanatory variable depends on the elevation gradient. In the present study, this gradient is relative small (minimum elevation is 4 m and maximum 1212 m).

The other external explanatory variable that has been explored in this study is related to the shadow cast caused by the topography. The slope and aspect effect on the measured values can not be evaluated in this study since the stations are located on horizontal surfaces. The sky-view factor influence, nevertheless, can be evaluated. Particularly, to assess this effect, a sky-view factor can be used. This sky-view factor can be defined as the ratio between radiation actually received by a planar surface to that received from the entire hemispheric radiating environment (without any obstruction). It represents the shadows cast by topographic features. Sky view factor can be derived from DEM using several available procedures. In the present study the sky-view factor was computed using the GRASS GIS [6] environment in the following way: given a location, the maximum elevation angle of sky obstruction were computed for 36 directions around this location. Then, a continuous curve of angle values was computed using linear interpolation. The area under this continuous curve, normalized to the entire hemisphere is considered the sky-view factor. Note that the value of the sky-view factor varies from 1, when the whole sky is obscured, to 0, when no obstructions are present. In actual cases, sky-view factor seldom are higher than 0.20.

In this study, a modified version of this sky-view factor was used. Particularly, the sky-view factor was computed just using the topographic information in the south direction. That is, the angles were only computed for the half of the sky view, from solar azimuth angles between 90° (eastern ) to -90° (western), instead of for the complete circumference (solar azimuth angles from -180° to 180°). We will call this new sky-view factor semi-sky-view factor hereinafter. As for the complete circumference, the semi-sky-view factor may take values between 0 and 1. Actual values for all the stations used in this study ranged between 0 and 0.195. This new explanatory variable reveled to be much more effective in explaining the solar radiation variability than a complete sky-view factor. The rationale behind this result is that, as it is known, in the northern hemisphere, the amount of radiation received from solar azimuth angles between below -90° and above 90° is scarce. Therefore, the topographic information associated with these angles is not relevant in explaining the solar radiation variability and just increases the noise of the explanatory variable, without adding new information. This new semi-sky-view factor was used as independent variable in the residual kriging procedure.

3. Results and Discussion

The Heliosat method is a technique of determining the global radiation at the ground by using data from a geostationary satellite.

In the Heliosat method it is assumed that the intensity of the visible solar irradiance which is scattered back to the satellite from the Earth and the atmosphere, behaves proportional to the atmospheric reflection. Also the isotropy of the atmospheric reflection is suppositional in order to disable the influence of the atmosphere’s heterogeneity on the reflection properties.

Due to the dominating dependence of the reflection on the cloudiness, it is feasible to derive an important quantity characterizing the degree of cloudiness existing within a solid angle from the radiation measured by the satellite. Via this quantity it is possible to deduce the transmission properties of the atmosphere and then determine the global irradiance.

Figure 1C shows a typical case of a clear day with the snow covering the Sierra Nevada Mountains. In these particular images, the method Heliosat-2 can lead to subestimations, because the pixels are considered to be covered by clouds instead of by snow. In this work, a preprocessing method is applied to perform a detection of possible snow covers. Consisting in a comparison between the mountain pixels versus the surrounding ones, where a very low albedo in the surrounding if compared with the mountain is considered to belong to a clear day with snow covers. The method offers a success of near 85% in the detection of snow covers and it will be used. Error reduction due to this detection is discussed in the Results section.

1.2. Horizon calculation

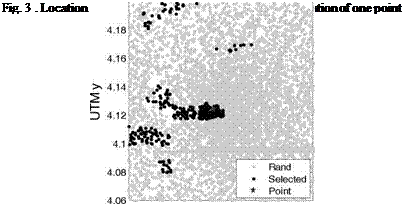Computational cost of the horizon calculation can be a problem when dealing with large areas; that issue has been addressed by developing an algorithm that reduces drastically the time spent in this process, without loosing much information about the actual horizon. The used DTM file contains around two million values of altitude, and the horizon for a specific point should be calculated by using all that information, but in this work most of the points are skipped and only around 70000 are utilized. The skipping step is defined as a function of the distance to the studied point, and a random contribution is also added. Finally, the horizon is only calculated for those selected points which altitude is higher than the studied point one, reducing the time consumption. Figure 3 shows the random and the selected points in the calculation of the horizon.

A comparison of the calculated horizon following the described algorithm and the real horizon (calculated by using the whole set of DTM points) appears in Figure 4, where it can be noted the little influence of the selection in the final calculation. Finally, for each day, the horizon will be overlaid with the sun path, obtaining the actual sunrise and sunset hours from the solar altitudes that will be introduced to the model.

2. Results and discussion

Daily irradiation values were calculated with and without inclusion of local effects; afterwards, the error was calculated in terms of Mean Bias Error (MBE) and Root Mean Square Error (RMSE), as a percentage of the mean measured value. Table 2 shows the obtained errors for the different stations and the three considered methods: A. Heliosat-2 with no horizon and using a mean altitude for the pixel, B. Heliosat-2 considering the calculated horizon and the altitude of the point and C. same as B but including the detection of clear days with snow covers.

Error reduction is detected for all the stations, and the importance of horizon effects appears to be larger than the effect of the snow covers. In fact, the consideration of snow covers is almost negligible in the case of the stations 13 and 14, as they are located in the plane area, outside the mountains, where snow is not usually present, but it can decrease up to 2% in the upper stations.

In addition, the station 9 is the one with a major improvement in the estimates, this is ought to the fact that is placed in a gully, having the larger horizon obstructions compared with the other stations. The mean RMSE considering the whole set of stations is reduced from 16% to 11%, verifying the good behaviour of the proposed methodology.

Once the performance of the method has been analyzed and in view of the satisfactory results provided in the global radiation estimates for the 14 stations located on a complex topography area, we generated a map with daily radiation values for the zone. Figure 5 shows a map created using this methodology.

3. Conclussions

Results obtained using the proposed method showed a good agreement with the measured ones and it is interesting to note that this procedure can be applied under all kind of sky conditions. A proposed method to calculate the horizon of a point was tested with satisfactory results.

The RMSE was diminished for the whole set of stations with a mean reduction of 4.7%. MBE was also improved, with almost no over or underestimation for most of the stations. It has been observed that the improvement in the estimates is small in plane areas with almost no horizon obstructions, but becomes significant in the locations inside the mountain. The effect of the snow was also studied and it was pointed out that for the stations in the upper area it could lead to a reduction of the RMSE up to 2%, being smaller or nil in the lower stations. Finally, the method was employed over a wide area allowing the generation of an irradiation map on a complex terrain. If no additional information would be considered, the HELIOSAT 2 model would give a fixed value for the whole pixel, taking into account a mean altitude of the pixel and no horizon. On the other hand, using this methodology, the topographic variability is included in the model and a map of irradiation can be made in an easy way for a complex topography site. In future works, this method is intended to be extended to the estimation of different components of the radiation (i. e. Direct Radiation, Photosynthetically Active Radiation PAR); and also to be used together with Artificial Neural Networks.

Acknowledgements

This work has been financed by the Ministerio de Ciencia y Tecnologia of Spain (projects ENE/2004- 0786-C03-01 and ENE2007-67849-C02-02). We would like to thank CIEMAT for the use of the satellite images.

References

[1] Dubayah and Van Katwijk, 1992. The topographic distribution of annual incoming solar radiation in the grand River basin. Geophys Res. Leter, 19, 2231-2234.

[2] Fu and Rich, 2000. A geometric solar radiation model and its applications in the agriculture and forestry. Proceedings of Second International Conference on Geospatial Information in Agriculture and Forestry, Lake Buena Vista.

[3] Diabate, L., Demarcq, H., Michaud-Regas, N. and Wald, L., 1988. Estimating incident solar radiation at the surface from images of the Earth transmitted by geostationary satellites: the Heliosat Project. International Journal of Solar Energy 5, 261-278.

[4] Dribssa, E., Cogliani, E., Lavagno, E. and Petrarca, S., 1999. A modification of the Heliosat method to improve its performance. Solar Energy 65, 369-377.

[5] Zarzalejo, L. F., 2006. Irradiancia solar global horaria a partir de imagenes de satelite. Serie: Coleccion Documentos CIEMAT. Editorial CIEMAT, Madrid (Espana).

[6] ESRA, 2000. The European solar radiation atlas. Vol. 1: Fundamentals and maps. Editado por: Scharmer, K. and Reif, J. Les Presses de l’Ecole des Mines, Paris (France).

Benchmarking of solar radiation products can be done in different ways. If a kind of reference data is available which is assumed to be the “truth”, the modelled data sets can be compared and ranked how well they represent the reference data. But there is not always reference data available: e. g. for solar radiation spatial products (maps). Here benchmarking can assess the uncertainty of mapping products by their cross-comparison.

For site specific time series there are a number of different measures for benchmarking. A first set is based on first order statistics. These are the well known bias, root mean square deviations, standard deviations, their relative values to the average of the data set and the correlation coefficient. They compare how well data pairs at the same point of time compare with each other. They are important if one needs an exact representation of real data, e. g. for evaluations of real operating systems or forecasts of solar radiation parameters.

This exact match is not always important, e. g. for system design studies. Here the similarity of statistical properties as frequency distributions is more important than the exact match of data pairs. The MESoR project therefore suggests a number of parameters based on second order statistics [6].

Besides a common set of measures the selection of valid pairs of data is of importance to achieve comparable results. Valid data pairs should have passed the quality control procedure as described above, measured global horizontal ground data should be above zero (valid measurement, sun above the horizon) and the modelled data should be valid. Average values (e. g. for relative bias or standard deviations) are calculated based on the valid data pairs. If averages from multiple stations are to be calculated, all data pairs should be treated with the same weight. Averages should be calculated from the complete data set and not from the single stations results. This gets relevant if the stations have different numbers valid data pairs.

A benchmarking exercise applying the measures and rules to available data bases within Europe will be done in the second half of 2008.

Benchmarking of angular distributions is yet difficult, as there are a number of different instruments available with very different characteristics in terms of number of sensors, acquired parameters

(irradiance, radiance, luminance), geometry of the measurement directions in the sky hemisphere, spectral sensitivity of the sensors, aperture angle, size and shape and the sensors and the sensors linearity and dynamics. Further, there are only very few measurements available so far.

Solar maps can be benchmarked in two ways, either point based or map based. The point based benchmarking is similar to the time series benchmarking. Data is extracted from the maps and compared to the measurements (“ground truth”). First and second order statistics can be applied. Map based cross comparison of solar radiation provides means for improved understanding of regional distribution of the uncertainty by combining all existing resources (calculating the average of all) and quantifying their mutual agreement by the means of standard deviation. A sample evaluation has been done with five spatial data bases: ESRA, PVGIS, Meteonorm, Satel-light and NASE SSE.

A set of benchmarks has been proposed to evaluate solar radiation forecasts. Depending on the application different methods to assess prediction quality are appropriate. For the users of the forecast the verification scheme should be kept as simple as possible and be reduced to a minimum set of accuracy measures. Statistical measures are similar to time series but need to be adapted to forecast specific issues. Forecast should not only be evaluated against the measured data but also against reference models as persistence or autoregressive models to show the advantage of a forecasting system. For forecasting not only the quality of the prediction of a single site is of interest but also the accuracy of prediction of an ensemble of distributed sites e. g. feeding into an electricity grid node.

L. Martin1*, E. Lorenz2, A. Sood2, L. F. Zarzalejo1, K. Suselj2,J. Polo1, A. Navarro1, R.

Marchante3

1 CIEMAT, Department of Energy, Av. Complutense n°22, Madrid, 28040, Spain
2 Oldenburg University, Germany Energy and Semiconductor Research Laboratory Energy Meteorology Group
3 IrSOLaV, Calle Santiago Grisolia (PTM) 2, Tres Cantos, 28045, Madrid, Spain
* Corresponding Author, luis. martin@ciemat. es

Abstract

Although considerable effort has been done to make use of solar energy efficiently from industrial revolution, expecting fossil fuels would run out in the future, only minimal resources have been directed towards forecasting incoming energy at ground level. However, the necessity to have forecasting models which could optimize the integration of solar thermal power and photovoltaic into electric grid within different sources of electric power generation will grow up as they gain recognition as an energetic resource in the near future. In this work an evaluation of ERA-40 reanalysis data from ECMWF and Weather Research and Forecasting (WRF) mesoscale model is done over 40 stations from Spanish National Radiometrical Network which belongs to the Spanish National Weather Service (AEMet). The evaluaton is done in a hourly and daily resolution just for the next time step in the case of WRF evaluation and for daily resolution in the case of ERA-40 data. The results from WRF model are compared with predictions from European Center for Medium Range Forecasting (ECMWF).

Keywords: EuroSun 2008, proceedings, formatting guidelines, styles

1. Introduction

Although considerable effort has been done to make use of solar energy efficiently from industrial revolution, expecting fossil fuels would run out in the future, only minimal resources have been directed towards forecasting incoming energy at ground level [1]. However, the necessity to have forecasting models which could optimize the integration of solar thermal power and photovoltaic into electric grid within different sources of electric power generation will grow up as they gain recognition as an energetic resource in the near future.

Photovoltaic and solar thermoelectric power are main sources of solar energy for electricity generation. Currently the potential market is huge and its development is being supported by agreements in Kyoto protocol and by progressive series of regulations regarding green energy (feed-in tariff) established in several countries like Spain and German [2]. In the case of Spain, current legislation (Royal Decree 436/2004, 12th of March) allows to minimize investment risks to promoters and to contribute opening up great perspectives to solar energy development.

Energy stock market participation is regulated by two basic rules: on the one hand it is necessary to predict the amount of energy which will be produced, up to 72 hours before, and on the other hand deviations of energy produced compared to programmed one are strongly penalized.

In this work a skill evaluation of the Weather Research and Forecasting (WRF) mesoscale model and ERA-40 reanalysis data from ECMWF is done over 40 stations from Spanish National Radiometrical Network which belongs to the Spanish National Weather Service (AEMet). The prediction is done in a hourly and daily resolution just for the next time step. The results from WRF model are compared with predictions from European Center for Medium Range Forecasting (ECMWF).

The SolData optics table was equipped to measure: global irradiance (3 instruments), ultraviolet B (UVB), illuminance (lux), barometric pressure (hPa), background radiation (counts/10 min), sky luminance (cd/m2) and PAR (einstein/m2). These measurements have been described in other work [5]. The focus of this paper is on further analysis of the global solar irradiance data. Other research groups on board the research vessel contributed to another database, and this database is also accessible (5-minute values) including relative humidity, a parameter which will also receive attention in this paper.

2.3

Global solar irradiance

Figure 2: Global solar irradiance from Accra, Ghana, October 2006.

Figure 2 shows typical global irradiance data — in this case when the expedition was near the Ghanan city of Accra off the western coast of Africa. We have focused on days which were “clear”, i. e. cloud cover was so insignificant that a clear day global irradiance model could be fitted to the global irradiance data for a given day. A significant number of days during the eight month voyage of Galathea III were so clear, that this procedure was possible.