Silicon is deposited by CVD on a layer of silicon powder. The deposited layer is easily separated from the quartz substrate owing to the presence of the powder layer and constitutes a self supported pre­ribbon. By ZMR processing this pre-ribbon is converted into a multicrystalline ribbon that can be used as substrate for solar cells.

 

6

 

3

 

5

 

4

 

1

 

2

 

Fig. 2. Experimental setup for the CVD deposition step.

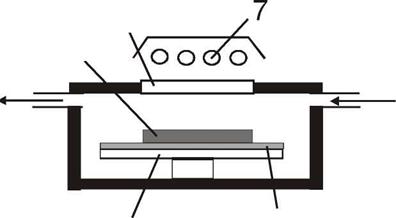
The CVD deposition step was tested so far in a specially designed batch mode furnace (see Fig.2). The substrate (1) is a single plate of quartz covered by a layer of silicon powder (2). It remains stationary in the central stage below the quartz window (6). The powder layer is heated by the radiation from halogen lamps (7); silane gas flows (4) through the furnace and thermally decomposes depositing silicon on top of the powder layer. Conditions in the furnace are set to ensure an approximately uniform growth of the deposited section of silicon (3) ribbon on top of the flattened powder layer (2).

2. Results

Several runs were performed to optimize CVD deposition conditions. It was observed that film porosities below ~50% allowed reproducible ZMR [3].

The SDS pre-ribbons produced during the CVD step are intrinsic. To be used as base material for solar cells they must be doped. We used a spray doping technique [4] to do the p-doping and ZMR in one step.

The recrystallized ribbons were 300 pm thick, with a crystalline structure consisting of grains of a few centimetres long and a few millimetres wide, p-doped, with resistivities of 1.5 Qcm.

We prepared very simple (no passivation nor anti reflection coatings) solar cells on this new material to assess the overall potentiality of the whole process.

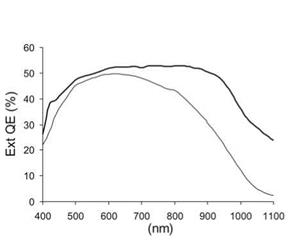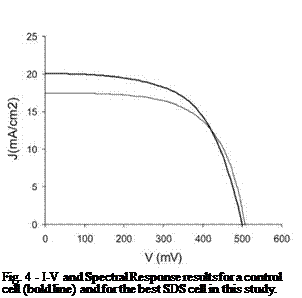
The lower values of the short-circuit current in SDS samples when compared to the control samples are in agreement with the lower quantum efficiency values in the infrared region of the spectrum in the Spectral Response measurements.

Nevertheless, the results on these first SDS solar cells, namely the obtained value for the diffusion length in the best SDS (70 pm) clearly demonstrate the ability to achieve high efficiencies.

4. Conclusion

The SDS-Silicon Dust Sheet method for the formation of silicon ribbons based on a gaseous feedstock was described, and the feasibility demonstrated by the preparation of full working photovoltaic cells on a SDS ribbon silicon. The advantages of the SDS process are (i) no substrate is required, thus reducing sources of impurity and cost; (ii) low energy budget because CVD is performed under atmospheric pressures and at low temperatures; (iii) high quality, free standing, crystalline silicon sheets are made possible by the non-contact float-zone crystallisation with in-situ doping.

5. References

[1] Wald F., Crystals: Growth, properties and applications 5, Springer: New York, 1981, 147-198

[2] Ciszek T., Silicon Processing for Photovoltaics I, North-Holland, 1987; 131-166

[3] Pinto C. R., Serra J. M., Brito M. C., Gamboa R., Maia Alves J., Vallera A. M., Proceedings of 21stEuropean Photovoltaic Solar Energy Conference and Exhibition, Dresden, 2006, 1099-1101

[4] Silva J. A., Brito M. C., Costa I., Maia Alves J., Serra J. M. and Vallera A. M., Solar Energy Materials and Solar Cells 2007; doi:10.1016/j. solmat.2007.08 .002