The reference building has a floor area of 1000 m2 (height: 6 m). It is facing south and has a flat roof. The floor slab consists of 20 — 60 cm concrete with integrated underfloor heating system and 10 cm of insulation underneath. Four different reference cases were defined corresponding to typical insulation and usage scenarios for industrial buildings. The used building parameters can be found in Table 1.

The so-called “Standard” reference building (Case 3) in the table is a relatively well insulated building with wall sections consisting of 160 mm of mineral wool insulation and 2 mm of sheet metal on both sides, for the roof 200 mm of mineral wool insulation was assumed. The windows are standard double-glazed insulating windows.

However, in retrofit situations, industrial buildings are often not very well insulated (sometimes not insulated at all). Therefore, a poorly insulated reference building was also defined with only 60 mm of mineral wool insulation in the walls and 100 mm in the roof (Cases 1 and 2). The air exchange rate in industrial buildings is especially difficult to estimate. It varies strongly depending on the number and duration of door openings. For this study, a standard air exchange rate of 0.3 h-1 was assumed. Case 1 includes an increased air exchange. In addition, another case with 8 kW of waste heat (e. g. of machine operation) during working hours was considered (Case 4).

The first step in the calculation of the number of collectors per row is to estimate the mass flow rate per row. To guarantee an appropriate heat transfer coefficient inside the absorber tube a turbulent flow is necessary. Taking into account that the conditions of the pre-design are good ones in terms of available solar energy, it is chosen a Reynolds number high enough to have turbulent flow even at any other solar radiation conditions — like in winter, for example-. It means to work with a Reynolds number around 600.000, since the useful thermal power in winter can be, in the worst cases, 30% lower than the one collected in summer, inducing a reduction of the mass flow rate to a third of the value in summer.

The mean fluid velocity, v, in the absorber tubes is calculated from the expression of the Reynolds number. A first estimation of the mass flow rate per row, m0, is given by

m0 = vp At (eq.1)

where p is the fluid density and At is the inner cross section of the steel absorber tube.

The number of collectors required in every row depends on the conditions set at the inlet and outlet of the solar field and the thermal power supplied by every collector. The increase of temperature between the inlet and outlet of every row, ATrow, should consider that the fluid temperature at its outlet has to be higher (7-10°C) than the temperature of the steam generated in the heat transfer fluid to water heat exchanger, in order to compensate the thermal heat losses through the pipe lines which connect the rows in the solar field, the efficiency of the heat exchanger and the pinch point of the latest. The energy given by a collector is assumed to be the same for every collector, independently what the position of the collector in the row is, i. e., the heat capacity of the heat transfer fluid, cP, and thermal losses are assumed to be constant in the range of working temperatures in a row.

To calculate the temperature increment in every collector, AT°kc, an energy balance is done

considering that the solar thermal power absorbed by the collector minus its heat losses to ambient is the useful thermal power, Qutii, coic, used to increase the temperature of the working fluid mass flow. Mathematically,

where Ac is the aperture area of a collector and T^s and Qloss are the absorber tube temperature and thermal losses, respectively.

Thus, the number of collectors, N, is given by the rate of the temperature increase needed per row, ATrow, and the temperature increase in every collector, AT°kc,

The obtained number of collectors per row, N may not be an integer. If so, this number has to be rounded to an integer number, Npre_design from which the new temperature increment in a collector in the pre-design, ATcol, is obtained from (eq.3) considering N=Npre-design and the new pre-design mass flow rate, mr, comes from (eq.2) considering AT°lec = ATcolec.

The second noteworthy outcome of this survey is the definition of the most suitable industrial sectors, where solar thermal heat could be fruitfully used. In these sectors, the heat demand is remarkable and more or less continuous throughout the year. Furthermore, as described above, the temperature level required by some of the processes is compatible with the efficient operation of solar thermal collectors.

The key sectors are food (including wine and beverage), textile, transport equipment, metal and plastic treatment, and chemical. The areas of application with the most suitable industrial processes include cleaning, drying, evaporation and distillation, blanching, pasteurisation, sterilisation, cooking, painting, and surface treatment. Finally, among the most promising applications space heating and cooling of factory buildings should be included as well [4].

The relevance of each sector regarding the solar thermal market development also depends on the local industrial profile; for example, breweries represent an important industry in Austria and Germany, while dairies are important in Italy and Greece.

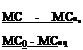The main purpose of the drying tests is to obtain a mathematical model that describes the performance of the dryer under any given condition. The drying curves can be modelled using theoretical or semi-theoretical equations [8]. The model expressions concern the simultaneous heat and mass transfer equations that describes the process. Moisture ratio equation is the common theoretical expression to model the drying process, described in Equation 1:

Where MC is the moisture content at any time, MC0 is the initial moisture content and MCeq is the equilibrium moisture content obtained as the asymptotic value of the weight of the sample when it remains constant [9].

Many researchers have described the solar drying process for common products like crops, fruit, leaves, etc. using different mathematical expression, all based on equation 1. The Page model equation, equation 2, resulted in a simple expression, similar to the theoretical expression that employs two constants: k and n, to describe with high degree of precision the woodchip drying performance [9]. Thus each drying test is described by two constants as it is shown in the table 2.

MR = exp(-ktn ) (2)

Table 2 shows the values of the constants k, n for 5 tests, described before in Table1, selected to build a global model that describes the drying process for woodchip. The statistical values, correlation coefficient, R, and mean square of deviations, X2, shows the good agreement between data and modelled values for the Page model.

The effects of temperature and drying velocity on the moisture ratio were investigated using a multiple regression analysis to account for the drying variables on the Page model constants. The values of constants к and n were regressed against those of drying air temperature and air velocity using multiple regression analysis. All possible combinations of drying variables were included and tested in the regression analysis [10]. The multiple combinations of different parameters which gave the highest R[7] [8] were finally included in the model. The model equation was as follows:

MR = exp(-(0.1288 • V + 0.0008) • (-0.0009 • T[9] [10] [11] + 0.5559 • T + -2.0808) • t(-9-5259V+3-3147V+Ы768)) (3)

Validation of the Page model was confirmed by comparing the estimated or predicted moisture ratio at any other particular drying condition. The validation of the Page model at different air temperatures and air velocities is shown in Figure 3, where the experimental data of 4 tests is compared with the predicted values obtained from the model giving a good fitness.

Fig 3: Comparison of experimental and predicted MR for 4 new tests.

on the transpired plate type: the collector was a wooden box that comprised a perforated absorber plate made of 1.6 mm thick Aluminium. The area of the collector is 1.80 m2 has been drilled forming a distribution of 2 mm diameter holes spaced 20mm apart. The lower section of the collector frame had 35 holes of 20 mm diameter for air inflow. At the rear backing plate on the top, the fan has been mounted to deliver the air into a 150 mm flexible duct. The gap between the bottom of the collector and the absorber plate was 110 mm. In addition, considering the operating temperatures predicted at higher levels of irradiance, the channelled transparent polycarbonate cover is held 4 cm from the absorber plate to minimise convective heat loss. [5]

The system design follows two different approaches. The first one is the “Compact System” for very low fresh water capacities between 100 and 500 l/day. The second one is a “Two-Loop System” for higher capacities.

Compact System

The low thermal capacity of MD-modules enables a quick change of feed volume flow and operation temperature without instabilities in the desalination process. Thus the MD-modules can directly be connected to a corrosion free solar thermal collector without any heat storage. Intermittent operation is possible without reasonable efficiency losses.

The main components of the Compact System are a 500 l feed storage (not represented in the sketch of Fig.4, left side), 1 MD-module, a 6- 7m2 sized solar thermal collector, a pump and a PV module for the electrical power supply of the pump and control system. While the feed storage is mounted above the collectors, most of the hydraulic components are installed in a closed housing covered by the back site of the collectors. However, the cold feed water is pumped into the condenser channel. Afterward the pre-heated feed water leaves the condenser outlet and enters the solar thermal collector which is directly connected to the condenser outlet. The feed temperature is increased by about 5 to 10 K and is re-circulated to the evaporator inlet. The advantage of this configuration is its simplicity and the good efficiency because there are no additional heat losses by a heat exchanger. The disadvantage is that no common flat plate collectors can be used, but the collectors must have sea water resistant riser and header tubes.

The distillate flows to a fresh water tank. The brine rejected from the evaporator outlet of the MD module is recirculated to the feed storage. So the salt concentration as well as the temperature of feed water in the feed storage increases over the day while the content of water decreases due to distillate production. The feed storage is refilled automatically when a certain level or temperature is reached.

Six Compact Systems were constructed, installed and operated since December 2004 in Pozo Izquierdo (Gran Canaria), Alexandria (Egypt), Irbid (Jordan), Kelaa (Morocco) and Freiburg (Germany). In December 2007 an improved compact system with a maximum daily capacity of 120 litres was installed in Tenerife, Spain (Fig. 4, right hand side).

Among other disadvantages with conventional solar collector systems there is the problem that nobody realizes if they work badly or not at all or even if a forthcoming failure is near. It is

suspected that at least one forth of all solar collector systems (in Germany) is practically out of order or has even more heat losses than harvest (gain). Installations without antifreeze must work nearly error-free. Otherwise their producer will be bankrupt soon. Therefore sophisticated and reliable diagnosis software is essential. The solar controller of the Paradigma AquaSystem has these functions since 2003 and works with the same software for single family houses as well as for industrial installations of any size. It is alarming but characteristic for the German solar market that these tools were not developed until they were technically necessary whereas both the producers of conventional solar installations and the distributors of subsidies have been making do with the high failure rate for many years.

Matthias Rommel

Fraunhofer Institute for Solar Energy Systems ISE, Heidenhofstr. 2, 79110 Freiburg, Germany

matthias. rommel@ise. fraunhofer. de

Abstract

A large share of the energy which is needed in commercial and industrial companies for production processes is below 250°C. Solar collectors for the temperature level up to 80°C are already on the market. But new and advanced collector technologies are needed for the higher temperature levels between 80°C and 250°C.

Several new development activities on process heat collectors have been started in the last years. Many, but of course not all of them were somehow linked to Subtask C of the IEA-SHC Task 33/Solar PacesIV "Solar Heat for Industrial Processes" which was carried out under the Solar Heating and Cooling Programme SHC of the International Energy Agency IEA. The paper gives an overview on these collector developments.

Also Fraunhofer ISE is involved in different collector development activities for process heat applications. In order to carry out high quality R&D work in this field together with the solar industry, a new collector testing facility was set up which allows to measure efficiency curves for collector operating temperatures up to 200°C.

Keywords: process heat collectors, industrial process, IEA SHC Task 33, SHIP, collector testing

1. Introduction

As reported by Weiss et al. in [1], the solar thermal collector capacity in operation worldwide in 2006 equalled 127.8 GWth corresponding to 182.5 million square meters at the end of the year 2006. Of this, 102.1 GWth were accounted for by flat-plate and evacuated tubular collectors and 24.5 GWth for unglazed plastic collectors. Air collector capacity was installed to an extent of 1.2 GWth.

The solar heat is mainly used in the household sector for domestic hot water and room heating. In contrast to that, the use in commercial and industrial applications is very limited up to now. On the other hand, the industrial sector in the OECD countries has the highest share of the total energy consumption, at approximately 30%. Solar heat for industrial processes is therefore an important field with a high potential of conventional energy savings, reduction of CO2 emission and economical interest for the solar thermal industry in Europe and world-wide.

A large share of the energy which is needed in commercial and industrial companies for production processes is below 250°C. Solar collectors for the temperature level up to 80°C are already on the market. But new and advanced collector techniques are needed for the higher temperature levels. Especially collectors for operating temperatures between 80°C and 250°C are of interest.

All cases shown above were calculated with an insulation layer of 10 cm underneath the floor slab. However, industrial buildings are often constructed without an insulation layer underneath the floor. The concrete floor is put directly on some kind of gravel to prevent the concrete from frost damage.

How much energy is lost through the floor slab of such a building depends on the physical parameters of the soil underneath. To illustrate the influence of an insulation layer underneath the floor slab and to show the influence of the soil characteristics, simulations were carried out with two extreme sets of soil parameters: very light and dry soil such as sand that doesn’t conduct the heat well and heavy wet soil such as clay that is much more dense and conducts heat well (see Table 2). As expected, the influence of the soil parameters on the heat demand of the building is much larger if there is no insulation layer underneath the building. However, the most important result is that the space heating demand is roughly doubled without an insulation layer underneath the building.

The next step is the calculation of the number of parallel rows, M. This value is a function of the thermal power required by the power block, Qt. The number of rows is the integer rate of this demanding thermal power, Qt, by the thermal power generated in a row, Qrow, which is given by the useful thermal power supplied by every collector, Qutil, colc, multiplied by the pre-design number of collector per row, Npredesign, i. e.,

2. Solar field optimization

In the northern hemisphere, the solar incidence angle in winter is larger than in summer. So the solar irradiation available on the solar field is smaller (due to the cosine effect) and then the generated power decreases too. To reduce this winter effect, the designer could increase the

number of rows, but it would add an overproduction of thermal energy in summer that can not be used by the power block. This wasted thermal energy is known as dumping of energy.

With the methodology proposed in this paper, the optimum size of the solar field is the one that produces the highest electrical power generation with the lowest dumping of energy (below 3%, [5]). To determine this optimum, simulations with several sizes of the solar field are run along a real year (i. e., introducing ambient temperature and solar irradiation data from a typical meteorological year). The sizes are around the already calculated number of rows, M, in the pre­design. A model of the solar thermal power plant is, therefore, necessary.

The model of the solar thermal power plant has two independent components: the solar field model and the power block model (Fig.1).

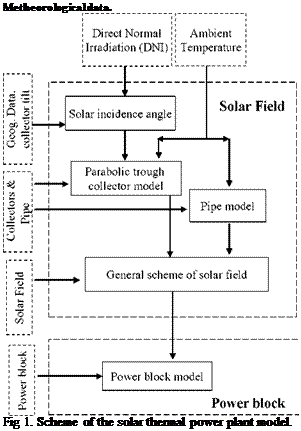For the solar field model the simulation program TRSNYS (TRansient SYstem Simulations), [6], has been used. This program has a modular structure, which allows of programming in blocks. The different blocks considered for the solar field models are (Figure 1): a thermal and hydraulic model of a parabolic trough collector, a thermal and hydraulic model of a pipeline connection between two collectors in a row, a solar incidence angle calculator and a block reporting the general arrange of the solar field (number of collectors per row and number of rows in the solar field).

It is advisable that the direct normal irradiance and ambient temperature data are mean values in 10 or 15-minute time periods, in order to account transient clouds. The maximum time step to record these meteorological data being considered useful enough is 1 hour. The hydraulic and thermal models of the parabolic trough collectors and their interconnecting pipelines are stationary models.

The thermal model uses the corresponding heat balance, while the hydraulic model calculates the pressure drop using the Bernoulli equation. The mass flow of the heat transfer fluid in the solar field is the one which assures at every moment (i. e., under typical beam irradiance and ambient temperature) a fixed solar field outlet temperature. This temperature is always below the maximum bulk temperature of the thermal oil used as working fluid in the solar field and is previously defined for the solar field pre-design, taking into consideration the efficiency of the oil to water heat exchanger and the steam temperature needed at the inlet of the turbine. At the inlet of the turbine, the temperature — and pressure — is considered to be constant, unlike the steam mass flow, which varies depending on the oil mass flow in the solar field.

The power block model considers the influence of steam mass flow variations at the inlet of the turbo-generator on its electric output. This influence is handled by a fitting curve obtained from the data given by the turbine manufacturer. A conventional fossil fuel boiler may be introduced if hybridization is considered.

The main results of the plant simulation are the incident solar energy onto the solar field, the useful thermal energy produced in the solar field and in the conventional boiler — if any-, the electrical energy generated in the turbine and the dumping of energy, all these results integrated along one year.

3. Example

As an example, let’s consider a parabolic trough solar power plant of 50 MWe somewhere in the South of Spain without storage. It is assumed that there are no restrictions or limitations in the size and orientation of the plot for the solar plant. The heat transfer fluid considered in this example is Therminol VP1 and the parabolic trough collector model is the ET-II (5.76m aperture width, 142.8m useful length). The orientation of the collectors is North-South. The Rankine cycle is assumed to have 38% gross efficiency (thus 131.6 MWth have to be supplied by the solar field at nominal conditions). The power block specifications determine that the temperature of the oil at the inlet and outlet of the solar field are 296°C and 393°C, respectively. 12% conventional fossil fuel energy supply is allowed in a yearly basis.

In the pre-design it is assumed a Direct Normal Irradiance of 850W/m2 and an ambient temperature of 25°C. The temperature difference at the outlet and inlet of the solar field and the used collector features determines that every row needs to have 4 collectors. The required thermal power defines that 74 rows are necessary if the calculation procedure explained in section 2 is applied.

In the optimization of the solar field, the meteorological data available are given in 1-hour time steps. An interpolation procedure has been followed to obtain 5-minute data sets. The accumulated annual direct normal irradiation is 2286 kWh/m2. Simulations are run for ±10% of number of rows to have a dumping of energy lower than 3%. Having in mind a central feed configuration of the solar field piping, an even number of rows are necessary, so the annual performances of the plant with 66, 74 and 82 rows are carried out.

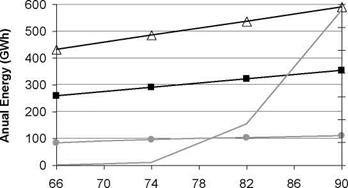
The annual solar energy onto the collector field (insolation), the thermal energy it produces, the electricity output of the power plant and the percentage of wasted energy is shown in Fig. 2 for different sizes of the solar field. As with 82 rows the dumping of energy was lower than 1%, the corresponding results for a plant with 90 rows are also obtained and shown. Running the plant simulation model with typical meteorological data for 74 rows a small dumping of energy is observed, becoming zero with 66 rows. Increasing the solar field size from 74 rows to 82 rows (10.8 %) the electric energy production increases 10%: from 94GWh to 103GWh. When the performance with 74 rows is compared with the one of 90 rows (21.65% of increase in size), the increase of the annual electric production is 17.2 % (from 94GWh to 110GWh), but with 3.37 % of dumping of energy. Thus the electricity production does not increase/diminish in the same percentage as the increase/reduction of the solar field size.

0s

> 

O)

5

c

<D

о

О)

с

‘о.

є

з

о

Fig 2. Incident, thermal, electrical and wasted energy as function of solar field size.

Keeping the criterion of being below 3 % dumping of energy, the optimized size of the solar field will be between 66 and 88 rows. The next step must be the economical evaluation of these few options.

4. Conclusions

In order to better design a parabolic trough power plant, simulation tools for finding out the optimal solar field size are necessary. Up to now, these simulation tools have an economical criterion as the only figure of merit, requiring a new optimization process every time there was any variation in the economical situation to apply. A way to reduce the number of cases to consider is by including another energetic criterion. This paper presents a methodology to optimize parabolic solar fields where an energetic criterion is applied prior the economical one. A first estimation of the solar field is obtained with a simple calculation, assuming representative meteorological conditions (pre-design). Taking this pre-designed solar field size as reference, annual evaluations of the performance of the plant with different sizes are analyzed. The limits where this size range stays are determined keeping the wasted energy (dumping), due to the oversizing of the solar field in summer, below 3%.

An example to illustrate how to proceed with a specific case is explained. After the methodology

presented here, the economical optimization that would follow is reduced to just a few cases.

References

[1] Greenpeace, SolarPACES, ESTIA: “Concentrated Solar Thermal Power Now — Exploiting the Heat from the Sun to Combat Climate Change”, September 2005

[2] X. Garcia Casals “La ene^a solar termica de alta temperatura como alternativa a las centrales termicas convencionales y nucleares”, 2001

[3] V. Quaschning, R. Kistner, W. Ortmanns, “Influence of Direct Normal Irradiance Variation on the Optimal Parabolic Trough Field Size: A Problem Solved with Technical and Economical Simulation”. ASME Journal of Solar Energy Egineering, 124 (2002) 160-164

[4] FLAGSOL, 2008, http://www. flagsol. com/FLAGSOL. htm, visited on August 2008

[5] J. I. Ajona, “Electricity Generation with Distributed Collector Systems”. Course: “Solar Thermal Electricity Generation”. Plataforma Solar de Almeria (13th-17th July, 1988).

[6] TRNSYS. A Transient System Simulation Program. Solar Energy Laboratory. University of Wisconsin. USA. (1994)

The results of the potential studies for different European countries are reported in the figure and the table below. The potential solar process heat estimated in the PROMISE study for Austria [5] reaches 5.4 PJ/year, while the Iberian Peninsula (Spain and Portugal, [6]) and the Italian studies [7] show a potential of 21 PJ/year and 32 PJ/year respectively.

The study carried out for the Netherlands shows a quite lower potential (<2 PJ/year). The reason for this is because the hot water production up to only 60 °C was assessed in twelve industry branches, thereby limiting the scope of the analysis.

In Table 1, the potential for the use of solar thermal in the industrial sector in different countries is reported in terms of delivered energy (PJ/year), capacity (GWth) and collector area (Mio m2). These potential figures are also compared to the corresponding industrial heat demand, in order to obtain the share of heat demand that could be covered by using solar thermal.

The results reported show that solar thermal systems could provide the industrial sector with 3^4% of its heat demand in Austria, Italy, Portugal, Netherlands and Spain.

Extrapolating this result to the European Union (EU 25), considering an average share of 3.8%, the potential for solar thermal applications in industry reaches a value for heat production of 258 PJ/year. The corresponding potential figures in terms of capacity and area have been calculated taking into account two possible yield values for the solar plants: 400 kWh/m2 year and 500 kWh/m2 year.

2. Conclusions

Even though solar thermal is used today mainly for providing hot water to households and pools, the conducted survey clearly highlights that, given its relevance in total final energy consumption, the industrial sector cannot be ignored.

Moreover, a remarkable share of its heat demand is needed in the low and medium temperature range, and this is true particularly for certain industrial sectors (food — including wine and beverage, textile, transport equipment, metal and plastic treatment, chemical) and for several processes (cleaning, drying, evaporation and distillation, blanching, pasteurisation, sterilisation, cooking, painting, surface treatment).

Studies based on both industry statistics and on case studies performed for assessing the solar thermal potential in industrial applications came to consistent outcomes regarding the share of low and medium temperature heat required by the industrial branches noted above.

The analysis of the surveyed country potential studies also shows that, even though using quite different methodologies, the obtained figures are quite similar and that solar thermal could provide the industrial sector with 3^4% of its heat demand.

This result allows the extrapolation of the national figures to the European level: solar thermal could provide 258 PJ/year of thermal energy to the EU25 industrial sector, which means an installed capacity of 100-125 GWth (143^180 Mio m2).

The most ambitious target for solar thermal, developed by ESTIF (European Solar Thermal Industry Federation), is to reach a level of 320 GWth installed in 2020, meaning about 1 m2 per capita and 19.7 Mtoe/year of energy delivered [8].

According to the European Solar Thermal Technology Platform (ESTTP), the goal for 2030 is to have installed a total capacity of 960 GWth by 2030.

Assuming that 10% of the calculated potential for solar heat in industrial applications were to be actually implemented within 2020, a total capacity between 10 and 12 GWth in industrial applications would give a contribution of 3^4% to the overall target of 320 GWth.

Following these assumptions, the industrial use of solar thermal energy could assure a market volume of 1,000 MWth/year, which would mean a 50% growth with respect to the current European annual solar market volume, that equalled 2,100 MWth (almost 3,000,000 m2) installed in 2006.

By exploiting this potential, 10,000-15,000 new jobs could be created by 2020. This figure represents a relevant share of the occupational target for the overall solar thermal sector, which according to the European Solar Thermal Technology Platform will be able to offer 224,000 full time jobs by 2020.

Even assuming a quite conservative scenario for the penetration of solar thermal use in the industrial sector, its contribution for reaching the EU set targets for 2020 is significant.

Finally, regarding future improvements of this analysis, new and more complete studies are needed within the EU framework to assess the detailed potential at national and EU levels in the different industrial sector and expand the current data available to solar thermal companies and policy makers.

References

[1] W. Weiss, I. Bergmann, G. Faninger, Solar Heat Worldwide — Markets and contribution to the energy supply 2005, International Energy Agency 2007.

[2] Data for 2004, based on EUROSTAT statistics.

[3] ECOHEATCOOL (IEE ALTENER Project), The European Heat Market, WP 1, Final report, Published by Euroheat & Power. www. ecoheatcool. org.

[4] D. Jaehnig, W. Weiss (AEE INTEC), Design Guidelines — Solar Space Heating of Factory Building with Underfloor Heating Systems, IEA Task 33/IV, 2007. Downloadable from www. iea- shc. org/task33/publications/index. html

[5] Muller, T. et al., PROMISE — Produzieren mit Sonnenenergie, Potenzialstudie zur thermischen Solarenergienutzung in osterreichischen Gewerbe — und Industriebetrieben within the Fabrik der Zukunft (BMVIT) Subprogram, Final report 2004.

[6] H. Schweiger et al., POSHIP (Project No. NNE5-1999-0308), The Potential of Solar Heat for Industrial Processes, Final Report.

[7] Solar thermal potential study for process heat in Italy, IEA Task 33/IV.

[8] European Solar Thermal Industry Federation, “Solar Thermal Action Plan for Europe”, www. estif. org.