In order to evaluate the performance of the AGMD modules, distillate production of each module was measured as a function of both hot and cold inlet flows and temperatures. Due to the transient nature of solar energy, it was not possible to control feed temperatures (hot temperature increased during a working day from 60 °C to 95 °C while cold temperature varies from 20 °C to 70 °C, approximately). Inlet flows were varied accordingly to a body centred multivariate experimental design (i. e., 5, 12.5 and 20 l/min).

Leakage was found at the very beginning of the experimental campaign (around 10-30% of leakage) depending on the hot inlet temperature and thus on the distillate production, leading to a distillate conductivity between 200-600 pS/cm, for that reason the amount of leakage was extracted from the distillate production in order to obtain a model to describe the performance of the system. Two months of experiments were carried out to obtain a single polynomial expression based on multiple linear regression, used to fit experimental data at 95% coefficients confidence interval level. The performance of individual AGMD module production, based on the polynomial expression, is depicted

in fig. 2 (correlation between predicted and observed values is acceptable at 95% confidence level). Leakage problems were solved by reassembling the modules. After that, the conductivity (although depending on hot inlet temperature) once achieved the stationary stage, was always around 2-3 pS/cm. No membrane scaling neither sings of membrane wetting was found during modules’ reassembling.

The strip dryers are operated with steam at 9 bar and have a capacity of 174 kW each. The advantage of this option is that all steam produced by the pilot plant can be utilized by a single consumer at all times, without the need to implement an additional storage. However, the 9 bar pressure level implies lower collector efficiencies and longer start-up times in comparison to the 4 bar applications. This drawback will be amplified by the solar radiation conditions at the given site, which will lead to significant proportion of part-load operation. Since the drying process is particularly sensitive for the product quality, this application was not considered appropriate for a first-of it’s kind demonstration plant.

Direct solar steam supply to the new production line

The current extension of the production facilities provides favourable conditions for the implementation of additional piping and heat exchangers for the solar steam into the degreasing and sealing baths and storage tank. Such a dedicated solar heating system would allow more flexibility for optimized operation of the solar field. It could be operated at temperatures little above the desired bath temperatures, and allow, in principle, even the implementation of non­tracking medium temperature collectors like CPC, vacuum tube or double glazed flat plate collectors as described by Rommel et al. [3] with pressurized water as the heat transfer medium.

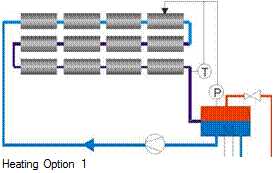
Figure 2 shows the hydraulic scheme for the direct supply of individual consumers by dedicated heat exchangers from the solar system. The solar field is operated in recirculation mode. Water from the bottom of the steam drum is pumped through the collectors, where a proportion depending on the solar input is evaporated. The water/steam mixture is returned to the drum where

it is separated by gravitation. Saturated steam is extracted through a pressure control valve and directed to the consumers. To ensure appropriate temperature levels in the process at all times, the solar heat supply will be backed up by heat exchangers fed by the conventional steam system (not indicated in Fig. 2), connected in series to the solar heat exchangers. The condensate is collected and pumped back to the steam drum. An expansion vessel is integrated into the system to compensate for the different volumes of water and steam in the cold and operation conditions, respectively. Auxiliary heating for freeze protection could be integrated into the steam drum or the condensate vessel.

Roof level

Installation level

Consumer 1 Consumer 2

Fig. 2: Hydraulic scheme of direct solar steam supply to individual consumers

Operating the solar system as an independent closed loop has several benefits. The conventional steam system cannot be jeopardized by transient insolation, condensate quality or fluctuating pressure from the solar system. Reducing the pressure and temperature may increase the of the collector efficiency by several percent.

On the other hand, the base load consumption of the new production line is too low to guarantee direct utilization of the solar steam (compare table 1). Therefore, costly steam storage would have to be integrated, or additional consumers need to be connected. Steam and condensate piping to several more or less distant consumers will not only increase the necessary investment but also cause thermal losses which may partly compensate the potential benefits from the reduced temperature operation of the solar field. Parallel steam supply from solar and conventional boiler system to the various consumers does also imply duplication of controls, leakage detection and

feedwater treatment, altogether leading to prohibitively high additional cost on top of the solar system.

Christoph Brunner1, Hans Schnitzer1,2, Bettina Slawitsch1, Werner WeiB3

1JOANNEUM RESEARCH Forschungsgesellschaft mbH — Institute of Sustainable Techniques and Systems

Elisabethstrasse 16, A-8010 Graz
Tel.: +43-316 / 876 2413, Fax: +43-316 / 8769 2413
E-Mail: bettina. slawitsch@joanneum. at
2 Institute for process engineering (IPE), Technical university Graz
Inffeldgasse 21, A-8010 Graz

3 AEE INTEC Feldgasse 19, 8200 Gleisdorf

Abstract

In the framework of the IEA Task 33 SHIP Solar Heat for Industrial Processes, several case studies were conducted to analyse the feasibility and the ideal integration of solar process heat for industrial companies. This effort was assisted by an Austrian national project „Styrian Promise (Production with solar energy) — Initiative for use of energy-efficiency and renewable energies (solar process-heat) in Styrian companies”. In Styria, 10 case studies were conducted in 2007 in order to develop concepts for energy conservation and for the implementation of solar heat. The suggested measures in terms of heat-integration, technological innovations and the use of solar process-heat result in savings that amount to more than 28 Mio. kWh/a for all 10 companies, implying an annual reduction of 5.830 t CO2. The economically recommended collector-area for those companies, for which the solar plant was thoroughly examined, was 2.790 m2 in total for 5 of 10 companies.

The work with industrial companies has proved that solar integration can be a good option for some industrial companies from an economic and technological point of view. However, the reduction of energy demand has to be the first step, before an efficient and sustainable solar process plant can be designed.

1. Introduction

In the framework of the IEA Task 33 SHIP Solar Heat for Industrial Processes, several case studies were conducted to analyse the feasibility and the ideal integration of solar process heat for industrial companies. This effort was assisted by an Austrian national project „Styrian Promise (Production with solar energy) — Initiative for use of energy-efficiency and renewable energies (solar process-heat) in Styrian companies”, which was funded by the Styrian government, FA3 Science and Research. This project was conducted under the lead of JOANNEUM RESEARCH Institute of Sustainable Techniques and Systems and in close cooperation with AEE INTEC and the Technical University of Graz.

Aim of the project „Styrian Promise“ was to explore the solar-thermal potential in Styria for industrial and commercial companies and to implement a reasonable combination, in energetic and

economic terms, of energy-efficiency and the use of renewable energy sources, especially solar process-heat, in Styrian production companies. The IEA Task 33 SHIP posed an excellent opportunity to discuss the project results on an international level and the Austrian experiences have also lead to important conclusions for the outcomes of subtask B within the IEA Task 33 SHIP.

In order to evaluate of the performance of the small mirror array, the MMA geometry and movement characteristics were implemented in a raytracing tool. The model includes a complete physical repre­sentation of the coupled movement of the facets of the array. For the simulation, a huge number of rays is generated and their paths are then traced (usually 108 rays). The effects considered in the model are:

• reflection off the glass cover, depending on the incidence angle and on the characteristics of the coat­ing (if applicable)

• absorption in the glass cover

• interaction of MMA components: moving mirror facets, sidewalls and back wall, specular reflection, at the mirror facets, mirror slope errors or facet tracking errors

• A further consideration of the model is the limitation of the angular movement of the MMA mirror facets due to mechanical constraints (e. g. facets hitting the sidewall).

• Instantaneous performance calculations are carried out based on a given direct normal insolation. Annual performance calculations are done by randomly distributing the generated rays over the time period of one year. Each ray has a specific energy according to the actual time and date, based on the instantaneous insolation and the total number of rays used. Integration over the year is then simply ob­tained by summing up the ray energies of each specific event. This is the preferred method since it is exact in principle, with accuracy limited only by the number of rays selected. Other options, such as the weighted summation of a limited number of selected times (e. g. one day per month with a given time period), require approximations to calculate the annual performance and are therefore less accu­rate. More information on the raytracing tool can be found in [4].

4.2. Assumptions

For the evaluation of the MMA performance, the following assumptions were made:

Mini-mirror array:

• box dimensions: (2 x 1)m (Ah = 2m2)

• reflectivity of the mirror facets: 94%

• glass cover: with antireflective coating (“ARC”) and without antireflective coating (“noARC”)

• number of facets: 5 x 10 (50 in total)

• facet dimensions: ideal: (0.2 x 0.2)m; no gap between facets, no movement limitations (“ideal”)

• facet dimensions: realistic: (0.18 x 0.185)m; gap between facets: 2mm, movement limitation by hit­ting sidewalls (“real”)

• no slope or tracking errors

In the ideal case, the possibility of facets touching each other or the sidewalls whenever they are not positioned parallel to the box cover is disregarded. This case defines an upper performance limit. In reality, the dimensions of the mirror facets and the gaps were selected to avoid the angular movement of the facets exceeding the angular movement limits given by geometric considerations. For the realis­tic geometry, the angle limit for the elevation axis is taken to be ± 25°. For the azimuth direction, the limiting angle is ± 48°. These angles are slightly larger than the angles that occur during the operation of the heliostat at this specific location. These angles may vary for other field locations or sites.

The antireflective coating of the glass has a solar-weighted transmittance of 97.3% at perpendicular incidence angles. This model is based on measurements of antireflective coated glazing.

Reference heliostat:

• two-axis tracking (azimuth/elevation)

• mirror dimensions: (2 x 1)m (Ah = 2m2)

• reflectivity of the mirror facets: 92%

• no slope or tracking errors

The reflectivity of the mirrors for the reference heliostat was selected to be 2% lower than that of the mini-mirror array, since the latter is installed in a closed box allowing the use of better and more sensi­tive materials.

Common Data:

• site location: 37.2° northern latitude (Seville, Spain)

• tower height: 100m

In both configurations, clean glass or mirrors were assumed. It is expected that dust will affect per­formance of both configurations in a similar way, so the trends will remain the same.

The basic data of some solar power tower plant in China are as follows,

Plant Location: 115.97° east, 40.47° north.

Tower Height: 100m, Ht = 85m, Tower Width: 10m.

Distance between mirror centre of heliostat and ground: 10m.

Mirror Height: 10m, Mirror Width: 10m.

Ratio of net area of mirror to area of heliostat: 0.95, Mirror Reflectivity: 0.9.

Receiver Aperture Height: 4m, Receiver Aperture Width: 4m.

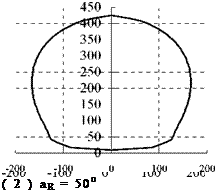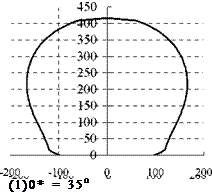
According to Fig.4 and formula (8), the receiver depression angle of this plant is 69.3o. Here, four heliostat field schemes whose receiver depression angles are 35o, 50o, 69.3o, 85o by respectively were compared and analyzed, field boundary lines are calculated by formula (1) to (7) and shown in Fig.5. Assumed that heliostats are arrayed as parallel and stagger pattern with same intervals, data are calculated and compared in Table 1.

( 1 ) aR = 69.3o ( 2 ) aR = 85o

Fig.5 Field boundaries with different aR

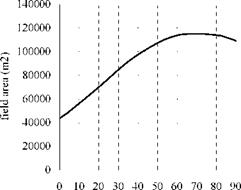
From Table 1 we can see that, the annual average field efficiency of the 4 schemes are subequal, with the maximum difference of 0.58%, and the field area of Scheme 3 is the largest one. The relationship between field area and receiver depression angle is shown in Fig.6(a). From Fig.6(a), we can known that the field area stays the maximum when receiver depression angle is about 70o.

However, for the pratical layout of the field, as the tower can hid the heliostats nearby, which can lead the heliostat and field efficiency decrease if heliostats are too near to the tower. Therefore, some distance should be left when the first row heliostats are arrayed, which has been reported earlier [7]. Considering this, the relationship between field area and receiver depression angle is shown as Fig.6(b) with a distance of 0.75Ht.

From Fig.6(b) we can know that, the field area changes little when the receiver depression angle is great than 70o. Moreover, according to the discussion above, it is known that there is a little change in annual average field efficiency when receiver depression angle is changed. As a matter of

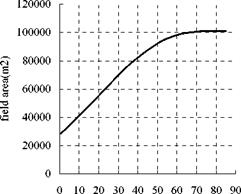experience, furthermore, radiation spillage can be reduced because of receiver with a depression angle in conditions that heliostats have tracking error and rocking error. Therefore, Scheme 3 is the optimal one, and the rationality of the formula of calculating receiver depression angle is validated at the same time.

Receiver Depression Angle Receiver Depression Angle

(a) (b)

Fig.6 Relationship between receiver depression angle and field area

2. Conclusion

Based on the geometrical optics theory, the function of heliostat field boundary line was deduced, and the simplified formula to calculate the receiver depression angle with the only independent variable of latitude was given. Moreover, a certain Solar Power Tower in China was taken as the case, the calculated heliostat field data were compared for different receiver depression angle, and the rationality of the formula was demonstrated. From the results, the following conclusions were drawn. For the conditions of the same heliostat dimension and arrangement, it is optimal when the receiver depression angle is at around the value calculated by the formula of receiver depression angle developed in this paper. At the same time, the installed capacity of plant is mainly dependent on the height of tower and the area of receiver aperture. That is, the installed capacity of plant increases with the height of tower and the area of receiver aperture. On the other side, the installed capacity of the plant almost has nothing to do with the receiver depression angle in a certain range around its optimum value.

References

[1] Field Layout and CPC Researches in Tower Solar Power Plants and Roof CPV Design [D]. GUO Su: College of Water Conservancy and Hydropower Engineering, Hohai Univ., 2006: 65-80. (in Chinese)

[2] F. M.F. Siala, M. E. Elayeb. Mathematical formulation of a graphical method for a no-blocking heliostat field layout[J]. Renewable Energy. 2001(23):77-92.

[3] Marcelino Sa’nchez *, Manuel Romero. Methodology for generation of heliostat field layout in central receiver systems based on yearly normalized energy surfaces[J]. Solar Energy, 2006 (80) :861-874.

[4] Vant-Hull, L. L., 1991. Concentrator optics. In: Winter, C. J., Sizmann, R. L., Vant-Hull, L. L. (Eds.), Solar Power Plants. Springer-Verlag, Berlin, ISBN 3-540-18897-5.

[5] Stine W B, Harrigan R W. Power from the Sun[Z].www. powerfromthesun. net,2005.

[6] J. A. Duffle, W. A.Beckman. SOLAR ENERGY THERMAL PROCESSES. John Wiley & Sons, 1974:1­

7.

[7] GUO Su, Liu Deyou. The Calculation of the Shadow and Block Efficiency of the Heliostats considering Tower Shadows in Tower SPPs[J]. Acta Energiae Solaris Sinica, 2007, 28(11):1182-1187. (in Chinese)

The parameters of the expander model are identified using test results. They are adjusted to fit the three model outputs (supply pressure, exhaust temperature, shaft power) to experimental data. The input variables of this calculation are: expander rotation speed, fluid flow rate, supply temperature and exhaust pressure. An error-objective function is defined, that should be minimized: this error function is a weighted sum of the relative errors for each output. It is defined as follows:

The parameters that minimize the objective function F are identified by means of a genetic algorithm. Given these parameters, the predicted and measured outputs can be compared:

• A maximum error of 3 K is reached for the prediction of the exhaust temperature.

• The supply pressure is predicted with a maximum relative error of 2.3%.

•

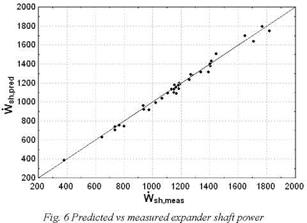The expander shaft power is predicted with a maximum deviation of 6% (Figure 6).

Once the geometrical relations of the reflector were established the design process started. It is difficult to divide this process into separate tasks because each particular solution strongly influences the range of the possible solutions for the whole system.

The main design challenge is how to manufacture and assemble a high precision optical device that could be easily integrated into building covers, with minimal or none on-site adjustments, maintaining manufacturing costs per square meter (or better per kWh generated) as low as possible.

To meet those requirements three elements are of critical importance:

1. The positioning system of the receiver

2. The reflector manufacturing and assembly process

3. The receiver performance.

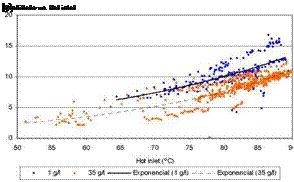
For the salt water experiments, the same factorial design was intended to be implemented, but the results (a significant raise in conductivity, with values ranging from 40-60 pS/cm) when working with low fluxes on both cold and hot channels, and regarding the leakage problems we already had in the first stage, made us decided to evaluate the performance at the best conditions that were settled on the first stage, those are 20 l/min on both channels, and thus only the effect of temperatures were checked. Generally, smaller distillate fluxes and higher conductivities were observed when working with salt water, about 20% less distillate production and regarding conductivity, the values for fresh water experiments were never above 10 pS/cm (average value of 3.97 pS/cm), while for salt water ones were never below 12 pS/cm with an average value of 61.7 pS/cm.

Fig.3. a) Comparison between fresh and salt water experiments of distillate conductivity versus hot inlet temperature, working at 20 l/min of flow rate. b) Comparison between fresh and salt water experiments of distillate production versus hot inlet temperature, working at 20 l/min of flow rate.

Fig.4. AGMD modules at PSA.

5. Conclusions

Main conclusions of the experimental campaign were the expected ones:

• The variable with higher contribution to the distillate production is the hot feed temperature as reported in literature [6] (increasing feed temperature makes distillate production higher due to the exponential increase of vapour partial pressure), followed by the hot flow rate and their interaction.

• Rising hot feed flow rate increases the heat and mass transfer coefficients in the boundary layer on the membrane surface, thereby reducing the temperature and concentration polarization effects, and as a result increasing the distillate flow [9].

• Cold side temperature and flow rate have a lower effect on the production than the hot side, for the case of flow rate the effect is almost negligible.

• Although MD is claimed to be not affected by salt concentration of the feed inlet, the results of the experiments reveal that not only the conductivity of the distillate but the production is negatively influenced by salt concentration.

References

[1] J. Koschikowski, M. Wieghaus, M. Rommel, Solar thermal-driven desalination plants based on membrane distillation, Desalination, 156 (2003) 486-587.

[2] E. Tzen et al., Desing of a stand alone PV-desalination system for rural areas, Desalination, 119 (1998) 327­334.

[3] K. Kalidasa, Kn. K.S. K. Chockalingam, K. Srithar, Progresses in improving the effectiveness of he single basin passive solar still, Desalination, 220 (2008) 677-686.

[4] Z. Ding et al., Analysis of a solar-powered membrane distillation system, Desalination, 172 (2005) 27-40.

[5] M. S. El-Bourawi et al., A framework for better understanding membrane distillation separation process, Journal of membrane science, 285 (2006) 4 -29.

[6] A. M. Alklaibi, N. Lior, Membrane-distillation desalination: status and potential, Desalination, 171 (2004) 111-131.

[7] R. Chouikh, S. Bouguecha, M. Dhabbi, Modelling of a modified air gap distillation membrane for the desalination of seawater, Desalination, 181 (2005) 257-265.

[8] M. N. Chernyshov, G. W. Meindersma, A. B. De-Haan, Modelling of a temperature and salt concentration distribution in membrane distillation feed channel, Desalination, 157 (2003) 315-324.

[9] F. Banat, R. Jumah and M. Garaibeh, Exploitation of a solar energy collected by solar stills from desalination by membrane distillation, Renewable Energy, 25 (2002) 293-305.

Integrating the solar generated steam directly into the existing steam line is a more promising option. In order to fit the solar boiler into the system identical technical standards as for the production steam line should be applied. This means that, for example, the piping materials used in the solar field have to be the same as in the production line, the chemical properties of the condensate should be the same, etc. In any case, due to safety regulations, the solar field and all the steam devices (valves, flexible hoses, steam drum, etc.) should have the “CE” mark and all welding must be done by classified welder for pressure equipment to pass the performance and acceptance test of the technical inspection agency.

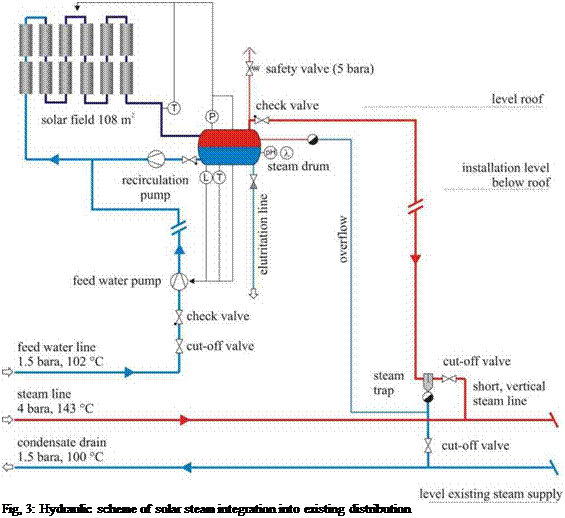If these basic requirements are fulfilled, the solar steam could directly feed into the production line by means of an overpressure valve (>4 bara), with the feed water to the solar steam generator provided from the industrial steam system. Condensate from the solar system can be tracked back by the condensate line of the existing system. The feed water pump for the solar field will be controlled by a level measurement in the steam drum. Figure 3 shows the system layout for this configuration. The steam drum is operated at constant pressure of about 4.3 bara.

During strong transients, that might have negative impact on the stability of the steam line, the generated steam can be blown off through a waste steam line above the roof. In this case, the production line is not affected. If the solar field is out of operation for an extended period, all condensate will be removed into a waste reservoir and the plant refilled with fresh feed water to avoid condensate degradation by corrosion and aging.

This option allows a very simple and compact balance of plant for the solar steam generator, and avoids cost and losses associated with additional piping and controls for the distribution. The solar steam generator is simply treated like any conventional supplementary boiler which might be retrofitted to an existing system.