A modified evacuated solar tube has been proposed, with a first development on the materials, fluid dynamic and design. It will not be enough to obtain the desired results in term of global efficiency, but it’s the first step to improve its characteristics. The model has been built in 2D-axial symmetry geometry, based on the real object realized for tests. The average velocity of the fluid is 0,0556 m/s, and water has been selected as a vector fluid. The solar tube has been modelled using k-s turbulence model, one of the most used for industrial applications. The model introduces two additional transport equation and two dependent variables: the turbulence kinetic energy, ke, and the dissipation rate of turbulence energy, sT. The k-s model [7] is described by the transport equation:

(12)

It is possible to derive an equation for sT and all terms that do not have an equivalent term in the ke equation are discarded. It results:

In which CEi, Cs2, Cke and o£T are turbulence model constants, respectively equal to 1.44, 1.92, 1.0, 1.3. г]т is the turbulent viscosity (Pa-s) and U is the average velocity field (m/s).

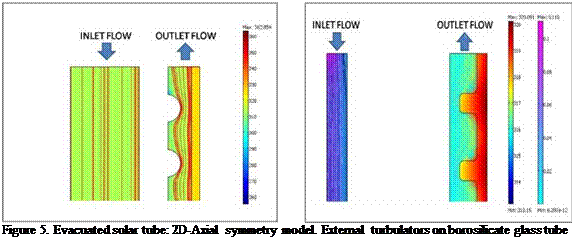The model constants are determined from experimental data. Some different models have been built, in order to verify different geometries within the same conditions applied in the real case model: fluid vector selection (water), the same inlet velocity, 0,0556 m/s, the same size of the model used (2-10-1 m). In order to have a higher turbulence effect it has been designed a pipe in which the fluid enters in the central part and exit through an annulus area. In the annulus area it have been designed a series of tabulators. Two models have been developed, in one model the turbulators are in the internal part of the tube (see Figure 4), in the second case they are in the external part, directly on the glass internal surface, in the opposite side of the cermet deposition (see Figure 5 and Figure 6).

Figure 4. Evacuated solar tube: 2D-Axial symmetry model. Internal turbulators.

The turbulation has an important effect, as it can be seen in the graph below. It increases the convective heat transfer lowering the thermal gradient between the cermet layer and the vector fluid. In the following figure it can be seen the difference between the turbulators on the internal tube and the turbulators on the external tube in the case of borosilicate glass or copper material used for the tube itself.

In the real model the temperature gradient is 19,2 K. In the different simulations it has been lowered until a value of 1, 06 K in the case of a copper tube below the cermet deposition and 2,97 K using a standard borosilicate glass. The reduction of the thermal resistance and of the temperature gradient has the effect to increase the thermal efficiency of the solar collector, mainly in the region between 273 and 373 K in temperature difference between the solar collector and the ambient, as reported in the figure 1, in the upper region "other losses". The estimated improvement in the global efficiency of the collector derived from the previous results can be about 10%.

3. Conclusions

The main objective of this paper is to show a proposal for a possible improvement to heat transfer losses on evacuated solar collectors to reach a higher efficiency and to meet the requirements to apply a thermodynamic cycle (i. e. Rankine or Stirling cycles). The use of a Stirling engine, for example, may allow the production of electrical power, together with a thermal power recovery from the same system. To reach such result it is necessary to obtain on the vector fluid higher temperatures, mainly above 473 K. At the moment part of the modelled work has been transposed to lab scale and the first measures have been taken. A full series of trials will follow, with a single tube and with a complete solar collector. The next step will be a deeper investigation through experimental activity. Another important aspect will be the optimization of the optics and of the concentrators. Thus, a research on cermet materials is starting with the objective to improve the efficiencies mainly in the temperature range of interest (473^573 K) for the proposed technology development. Our research will move on the development of nanostructured layers with possible different and improved optical performance in terms of thermal stability, emissivity (mainly above 473 K), and transmittance [3], [4].

The authors are indebted with Kloben (Turco Group S. r.l.) for partially funding this research. The cooperation between Kloben and Fondazione Bruno Kessler has produced four patents pending for international extension.

References

[1] D. Y. Goswami, S. Vijayaraghavan, S. Lu, G. Tamm, New and emerging developments in solar energy, Solar Energy 76 (2004) 33-43.

[2] L. J. Shah, S. Furbo, Theoretical flow investigation of an all glass evacuated tubular collector, Solar Energy 81 (2007) 822-828.

[3] L. J. Shah, S. Furbo, Vertical evacuated tubular-collectors utilizing solar radiation from all directions, Applied Energy 78 (2004) 371-395.

[4] F. P. Incropera, D. P. DeWitt, Fundamentals of Heat and Mass transfer, 4th ed., John Wiley & Sons LTD, 1996.

[5] P. Oelhafen, A. Schuler, Nanostructured materials for solar energy conversion, Solar Energy 79 (2005) 110-121.

[6] D. Xinkang et al., Microstructure and spectral selectivity of Mo-Al2O3 solar selective absorbing coatings after annealing, Thin Solid Films (2007), doi:10.1016/j. tsf.2007.07.193.

[7] B. Mohammadi, o. Pironneau, Analysis of the K-Epsilon Turbulence Model, John Wiley & Sons LTD, 1994.