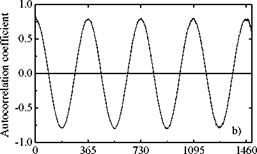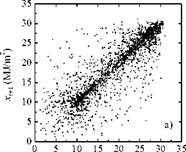
The first step in any analysis of chaotic data is to reconstruct an attractor (defined as set of points in phase space visited by a signal trajectory after transients are gone) from the data. Taken [6] suggested a method of phase space reconstruction that is known as the method of delays. This method consists of embedding the time series into a d-dimensional space, ^d, which is equivalent to the original unknown phase space composed of all the dynamical variables. Figure 1a shows the lag space plot for the global solar radiation time series using a lag of one. Points are distributed around a 45° straight line denoting a periodic nonchaotic time series. This is also evidenced observing the correlogram showed in Fig. 1b. An annual cycle of 365 days is presented. This is an expected result as the daily values of solar radiation are mainly affected by the earth motion.

xt (MJ/m2) Lags (days)

Fig. 1. a) Phase space structure of the global solar radiation time series using lags of one; b) Correlogram for

the global solar radiation time series.

In order to remove periodicity and trend, a transformation of the time series is undertaken by differencing. The new data are arithmetic differences between pairs of observations using a lag of one day (Axt = xt+I — xt). The differenced time series is denoted as {Axt}. Figure 2a shows the phase space plot for the differenced time series. The periodic pattern shown in the above figure seems to be removed. This result is corroborated analysing the correlogram displayed in Figure 2b. Autocorrelation coefficients fall to within the random-like zone after the first lag and, for the most part, remain in that zone thereafter. It is thus assumed that periodicity is removed.

Although point distribution in Fig. 2a seems to be due to some non-random complex underlying behaviour, the presence of a chaotic attractor in that phase space is not clear. To search the
optimum time delay г we have used the method of mutual information [7]. Mutual information, like autocorrelation, tries to measure the extent to which values Axt+m are related to values of Axt, at a given lag. However, mutual information has the advantage of using probabilities, rather than a linear basis, to asses the correlation and thus, nonlinear correlations are taken into accounts. The software implementation of that algorithm (and of those used hereafter) is from the TISEAN package [8].

400

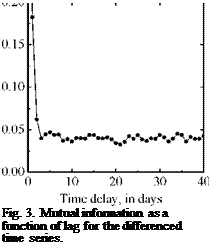As a prescription, a good candidate for the time delay г will be where the first marked minimum of mutual information occurs. From Fig. 3 it is noted that the first minimum is for г = 3. Once the time delay is chosen, the next step is to select the embedding dimension. Kennel et al. [9] introduce the method called the false nearest neighbors, which calculates the minimal embedding dimension. Two points in a d-dimensional phase space are false neighbors, in the sense of some distance function, when the distance, ||xjd — x/||, is small but the distance ||xi+1d+1 — Xj+1d+1|| in a d+1- dimensional phase space is not. Given a distance function, the Euclidean distance in our case, and some threshold size, the percentage of false near neighbors becomes zero as the dimension of phase space goes to the minimal embedding dimension. Figure 4 shows the percentage of false nearest neighbors as a function of the embedding dimension d. The main characteristic is that the fraction of false nearest neighbors does not fall to zero as d increases. This implies that the differenced time series has residual ‘noise’ in it, and thus the existence of low dimensional chaos is to be discarded.