1.2. Energy and Exergy

The operation of a typical TES can be separated into three key segments: charging, discharging, and storage. The energy balance within the TES adheres to First Law conservation of energy, such that:

tit t

f Estored)dt = f Echarged(t)dt “ f ^schargedW^ “ f Elost(t)dt

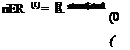Elost(t) denotes the thermal energy lost to the surroundings. We otherwise ignore kinetic and potential energy effects. Early techniques for assessing thermal storage effectiveness consisted principally of First Law considerations [6], where the Energy Response (pER) of an experimental TES would be typically compared to an ideal system [1], such that:

It has been widely accepted that the energy response alone (a representation the First Law of Thermodynamics) cannot solely characterize a TES. Stratification, for instance, which is known to significantly improve the effectiveness of a thermal energy store [7], cannot be assessed using the First Law as it is a characteristic that describes how energy is stored in the tank, not the energy content itself. To incorporate stratification into a characterization scheme therefore requires the Second Law of Thermodynamics, which states that the optimal storage of useful energy in a TES is achieved when maximing the exergy stored [5], represented as:

T0 refers to the dead-state temperature at which work is to be performed. A review of TES characterization methods by Haller et. al. [8] further illustrates that the incorporation of Second Law figures of merit can improve the overall assessment of TES storage efficacy. The methods by Panthalookaran [1], Shah and Furbo [2], and Huhn (referenced in [8]) are particularly highlighted.